Введение
Данное пособие содержит около двухсот геометрических задач с практическим содержанием, среди которых:
– задачи на нахождение расстояний с использованием теоремы Пифагора;
– задачи на нахождение углов;
– задачи, сводящиеся к нахождению длин дуг окружности;
– задачи на нахождение расстояний до недоступных объектов с использованием подобия;
– задачи на нахождение расстояний и углов с использованием табличных значений тригонометрических функций;
– задачи на нахождение площадей плоских и площадей поверхностей пространственных фигур;
– задачи на нахождение объемов пространственных фигур и др.
Решение геометрических задач с практическим содержанием позволяет:
– усилить практическую направленность изучения школьного курса геометрии;
– выработать необходимые навыки решения практических задач, умения оценивать величины и находить их приближенные значения;
– сформировать представления о соотношениях размеров реальных объектов и связанных с ними геометрических величин;
– выработать навыки работы с таблицами и другими справочными материалами;
– повысить интерес, мотивацию и, как следствие, эффективность изучения геометрии.
Предлагаемые задачи сопровождаются рисунками, позволяющими лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления.
Во второй части пособия даны ответы и решения ко всем задачам. В качестве приложения приведена таблица приближенных значений тригонометрических функций.
Отметим, что в задачах с приближенным ответом разные решения могут приводить к различным приближенным ответам. Поэтому правильным считается не только ответ, указанный в пособии, но и приблизительно равный ему ответ.
Пособие может быть использовано в качестве дополнительного сборника задач при изучении геометрии в 7-11 классах, при организации обобщающего повторения в 10-11 классах, в работе кружков, курсов по выбору или элективных курсов по геометрии, а также при подготовке к ГИА и ЕГЭ по математике.
Содержание
Введение………………………………………………………..
1. Расстояния. Теорема
Пифагора ………………………………
2. Углы
……………………………………………………………
3. Окружность
……………………………………………………
4. Подобие
………………………………………………………..
5. Тригонометрические
функции ………………………………
6. Площадь
……………………………………………………….
7. Объем
………………………………………………………….
Ответы ………….
…………………………………………….
1. Расстояния. Теорема Пифагора
1.
На
одной прямой на равном расстоянии друг от друга стоят три телеграфных столба.
Крайние находятся от дороги на расстояниях 18 м и 48 м. Найдите расстояние, на
котором находится от дороги средний столб.
2.
На
одной прямой на равном расстоянии друг от друга стоят три телеграфных столба.
Первый и второй находятся от дороги на расстояниях 15 м и 20 м. Найдите
расстояние, на котором находится от дороги третий столб.
3.
Мальчик
прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел
600 м. На каком расстоянии от дома оказался мальчик?
4.
Девочка
прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла
300 м. После этого она повернула на восток и прошла еще 100 м. На каком
расстоянии от дома оказалась девочка?
5.
Мальчик
и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам,
мальчик со скоростью 4 км/ч, девочка – 3 км/ч. Какое расстояние (в км) будет
между ними через 30 мин?
6.
Два
парохода вышли из порта, следуя один на север, другой на запад. Скорости их
равны соответственно 15 км/ч и 20 км/ч. Какое расстояние будет между ними через
2 ч?
7.
Используя
данные, приведенные на рисунке, найдите расстояние в метрах между пунктами A и B,
расположенными на разных берегах озера.
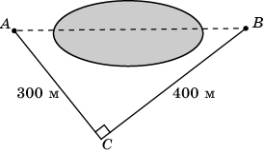
8.
Лестница
длиной 12,5 м приставлена к стене так, что расстояние от ее нижнего конца до стены
равно 3,5 м. На какой высоте от земли находится верхний конец лестницы?
9.
На
какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина
которой 13 м, чтобы верхний ее конец оказался на высоте 12 м?
10.
Какой длины должна быть лестница, чтобы она
достала до окна дома на высоте 8 метров, если ее нижний конец отстоит от дома
на 6 м?
11.
В 60 м одна от другой растут две сосны.
Высота одной 31 м, а другой – 6 м. Найдите расстояние между их верхушками.
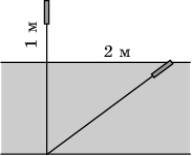
12.
Стебель камыша выступает из воды озера на 1
м. Его верхний конец отклонили от вертикального положения на 2 м, и он оказался
на уровне воды. Найдите глубину озера в месте, где растет камыш.
13.
Из круглого бревна нужно вырезать брус с поперечным
сечением 5х12 (см). Какой наименьший диаметр должно иметь бревно?
14. Отношение высоты к ширине экрана телевизора равно 0,75. Диагональ равна 60 см. Найдите ширину экрана.
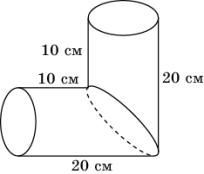
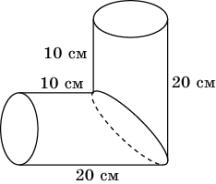
15. Какого наименьшего диаметра должен быть цилиндрический сосуд, чтобы в него можно было поместить деталь в форме прямоугольного параллелепипеда с размерами 6х8х10 (см)?
16. Туннель имеет форму полукруга радиуса 3 м. Какой наибольшей высоты должна быть машина шириной 2 м, чтобы она могла проехать по этому туннелю? В ответе укажите приближенное значение в метрах с точностью до одного знака после запятой.
17.
Какое наименьшее ребро должна иметь
кубическая коробка, чтобы в нее поместился тетраэдр с ребром, равным 8 см? В
ответе укажите целое число сантиметров.
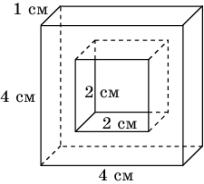
18.
В одном углу кубической коробки с размерами
40х40х40 (см) сидит муха. В противоположном углу сидит паук. Найдите длину
кратчайшего пути по поверхности коробки, по которому паук может доползти до
мухи. В ответе укажите приближенное значение, равное целому числу сантиметров.
19.
В одном углу комнаты с размерами 4х5х3 (м),
сидит муха. В противоположном углу сидит паук. Найдите длину кратчайшего пути
по поверхности комнаты, по которому паук может доползти до мухи. В ответе
укажите приближенное значение в метрах с точностью до одного знака после
запятой.
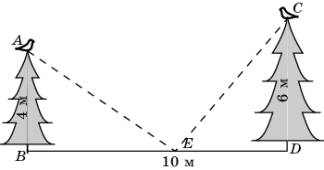
20.
На вершинах двух
елок сидят две вороны. Высота елок равна 4 м и 6 м. Расстояние между ними равно
10 м. На каком расстоянии BE нужно положить сыр для этих ворон, чтобы они находились
в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковыми?
2. Углы
1.
Колесо
имеет 18 спиц. Найдите величину угла (в градусах), который образуют две
соседние спицы.
2.
Сколько
спиц в колесе, если углы между соседними спицами равны 18о?
3. Колесо зубчатой передачи имеет 72 зубца. Сколько градусов содержится в дуге окружности, заключенной между серединами двух соседних зубцов?
4.
Сколько
зубцов имеет колесо зубчатой передачи, если дуга окружности этого колеса,
заключенная между двумя соседними зубцами, равна 12о?
5.
Какой угол (в градусах) образуют минутная и
часовая стрелки часов в 5 ч?
6.
Какой
угол описывает минутная стрелка за 10 мин?
7.
Какой
угол описывает часовая стрелка за 20 мин?
8.
На какой угол поворачивается минутная стрелка
пока часовая проходит 1о30’?
9.
Сколько оборотов в минуту делает зубчатое
колесо с 32 зубцами, если сцепленное с ним зубчатое колесо с 8 зубцами делает
12 оборотов в минуту?
10.
Диаметры двух зубчатых колес относятся как
3:8. На какой угол повернется большее колесо при одном обороте меньшего?
11. Зубчатое колесо имеет 12 зубцов. Сколько зубцов имеет сцепленное с ним второе зубчатое колесо, если при одном обороте первого колеса второе поворачивается на угол 120о?
12. На сколько градусов повернется Земля вокруг своей оси за 8 часов?
13. За сколько часов Земля повернется вокруг своей оси на 90о?
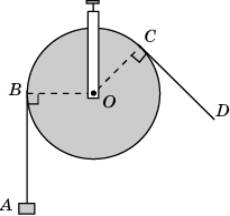
14.
Груз A висит на шнуре, перекинутом
через блок, изображенный на рисунке. Угол BOC равен 135о. Чему
равен угол между прямыми AB и CD?
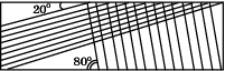
15.
Найдите угол, образованный линиями насечек у
напильника, изображенного на рисунке.
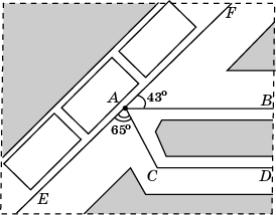
16.
На плане города улицы,
обозначенные как AB и CD,
параллельны. Улица EF составляет
с улицами AB и AC углы
соответственно 43
и 65
. Найдите угол, который образуют между собой улицы AC и CD.
17.
Для измерения углов артиллеристы употребляют
особую единицу, которую называют тысячной. В трехстах шестидесяти градусах
содержится 6000 тысячных. Сколько тысячных содержится в 1о30’?
18.
Для измерения углов артиллеристы употребляют
особую единицу, которую называют тысячной. В трехстах шестидесяти градусах
содержится 6000 тысячных. Сколько градусов составляют 100 тысячных?
19.
Угол в 1,5о рассматривают в лупу,
увеличивающую в четыре раза. Какой величины кажется угол?
20.
Окружность морских компасов делится на 32
равные части, называемые румбами. Сколько градусов составляют 4 румба?
3.
Окружность
1.
Длина
окружности равна 60 см. Найдите длину дуги этой окружности, содержащую 18о.
2.
За
длину окружности вавилоняне принимали периметр правильного шестиугольника,
вписанного в эту окружность. Найдите приближение для 
, которым пользовались вавилоняне.
3.
Шар
диаметром 1 м откатился по прямой на 10 м. Сколько полных оборотов он сделал?
4.
Поезд
едет со скоростью 81 км/ч. Диаметр его колеса равен 120 см. Сколько оборотов в
минуту делает колесо поезда? (Примите 
.)
5.
Какова скорость поезда (в км/ч), если диаметр
его колеса равен 120 см и оно делает 300 оборотов в минуту. (Примите 
.)
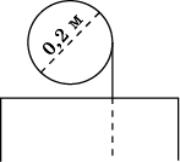
6.
При поднятии воды из колодца вал делает 20
оборотов. Найдите глубину колодца (в метрах), если диаметр вала равен 0,2 м.
(Примите 
.)
7.
Сколько оборотов должен сделать вал, чтобы
поднять воду из колодца глубиной 9 м, если диаметр вала равен 0,2 м? (Примите 
.)
8.
Длина
минутной стрелки часов на Спасской башне Московского кремля приблизительно
равна 3,5 м. Найдите длину окружности (в метрах), которую описывает конец
минутной стрелки в течение одного часа. (Примите 
.)
9.
Длина
минутной стрелки часов на Спасской башне Московского кремля приблизительно
равна 3,5 м. Какой путь (в сантиметрах) проходит ее конец за 1 мин? (Примите 
.)
10.
Длина минутной стрелки часов на Спасской
башне Московского кремля приблизительно равна 3,5 м. За сколько минут ее конец
пройдет путь длиной 105 см? (Примите 
.)
11.
Телега проехала 5,4 км. Диаметры ее переднего
и заднего колес равны соответственно 60 см и 90 см. На сколько больше оборотов
сделает переднее колесо по сравнению с задним? (Примите 
.)
12.
Диаметры переднего и заднего колес телеги равны
соответственно 60 см и 90 см. Какое расстояние (в метрах) проехала телега, если
ее переднее колесо сделало на 100 оборотов больше, чем заднее? (Примите 
.)
13.
Длина экватора земного шара примерно равна
40000 км. На сколько метров увеличился бы этот экватор, если бы радиус земного
шара увеличился на 1 м? (Примите 
.)
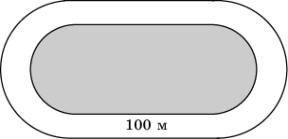
14.
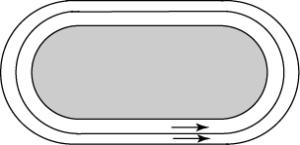
Поле стадиона имеет форму прямоугольника с
примыкающими к нему с двух сторон полукругами. Длина беговой дорожки вокруг
поля равна 400 м. Длина каждого из двух прямолинейных участков дорожки равна
100 м. Найдите ширину l поля стадиона. В ответе
укажите l
.
15.
Два спортсмена должны пробежать один круг по
дорожке стадиона, форма которого – прямоугольник с примыкающими к нему с двух
сторон полукругами. Один бежит по дорожке, расположенной на 2 м дальше от края,
чем другой. Какое расстояние должно быть между ними на старте, чтобы
компенсировать разность длин дорожек, по которым они бегут? (Примите 
.)
16.
Москва и Новороссийск расположены примерно на
одном меридиане под 56о и 44о
северной широты соответственно. Найдите расстояние между ними по земной
поверхности, считая длину большой окружности земного шара равной 40000 км. В
ответе укажите целое число километров.
17.
Расстояние между Москвой и Вашингтоном,
измеряемое по большой окружности поверхности Земли, примерно равно 7800 км.
Найдите примерную величину соответствующей дуги большой окружности, считая
длину всей окружности равной 40000 км. В ответе укажите целое число градусов.
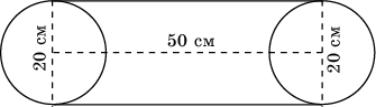
18.
Какой длины должен быть приводной ремень,
соединяющий два шкива с диаметрами 20 см, если расстояние между их центрами
равно 50 см? (Примите 
.)
19.
Столяру нужно сделать круглый стол на 6 человек.
Каким должен быть диаметр стола (в сантиметрах), чтобы на каждого из сидящих за
столом шести человек приходилось 80 см по окружности стола? (Примите 
.)
20.
Какое наибольшее число людей
можно рассадить за круглым столом радиуса 1 м так, чтобы на каждого человека
приходилось не менее 60 см длины дуги окружности стола? (Примите 
.)
21.
Водопроводная труба имеет в обхвате 246 см и
толщину стенок 2 см. Найдите внутренний диаметр сечения трубы. (Примите 
.)
22. Двадцать стальных шариков диаметром по 16 мм каждый находятся в подшипнике. Используя таблицу тригонометрических функций, найдите радиус внутреннего круга подшипника.
23.
Под каким углом
человек видит ноготь своего указательного пальца вытянутой руки, если ширина
ногтя примерно равна 1 см, а расстояние от него до глаза человека примерно
равно 60 см? В ответе укажите целое число градусов. (Примите 
.)
24.
Стрелок из лука видит мишень диаметра 120 см
под углом 1о. Найдите расстояние до мишени. Укажите приближенное
значение, выражаемое целым числом метров. (Примите 
.)
25.
Человек среднего роста (1,7 м) виден издали под
углом 12’. Найдите расстояние до него. В ответе укажите целое число метров.
(Примите 
.)
26.
Телеграфный столб высотой 8 м виден под углом
30’. Найдите расстояние до него. В ответе укажите целое число метров. (Примите 
.)
27.
Луна видна с Земли под углом 30’. Найдите
приближенное расстояние до Луны, зная, что ее диаметр приближенно равен 3400
км. В ответе укажите целое число километров. (Примите 
.)
28.
Солнце видно с Земли под углом 30’. Найдите
приближенное расстояние до Солнца, зная, что его диаметр приближенно равен
1300000 км. В ответе укажите целое число километров. (Примите 
.)
29.
Расстояние от Земли до Луны приблизительно
равно 408000 км. Диаметр Земли приближенно равен 13000 км. Найдите примерный
угол, под которым Земля видна с поверхности Луны. В ответе укажите целое число
градусов. (Примите 
.)
30.
Под каким углом виден самолет, длина которого
равна 30 м, пролетающий над наблюдателем на высоте 9000 м? В ответе укажите
приближенное значение в минутах. (Примите 
.)
4.
Подобие
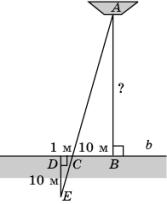
1.
Используя данные, приведенные на рисунке,
найдите расстояние AB от лодки A до
берега b.
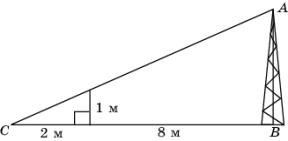
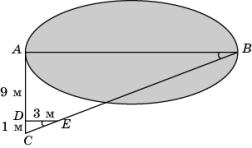
2.
Используя данные, приведенные на рисунке,
найдите высоту мачты AB.
3.
Используя данные, приведенные на рисунке,
найдите ширину AB реки.
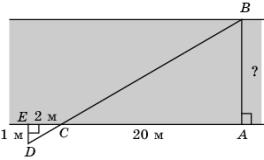
4.
Используя
данные, приведенные на рисунке, найдите ширину AB озера.
5. Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте расположен фонарь?
6.
Человек
ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на
высоте 5,4 м. Найдите длину тени
человека в метрах.
7.
Для
нахождения высоты египетской пирамиды недалеко от нее был установлен шест
длиной 1,5 м. Его тень составила 1 м. В тот же момент тень пирамиды была равна
96 м. Чему равна высота пирамиды?
8.
Чтобы
измерить высоту дерева, ученик держит линейку в вертикальном положении на
расстоянии вытянутой руки. Расстояние от глаза ученика до линейки равно 60 см.
Часть линейки, закрывающая дерево, составляет 20 см. Расстояние от ученика до
дерева равно 18 м. Чему равна высота дерева?
9.
Изображение
дерева на фотопленке имеет высоту 15 мм. Найдите высоту дерева, если расстояния
от объектива фотоаппарата до изображения и до дерева равны соответственно 50 мм
и 60 м.
10.
Столб высотой 15 м закрывается монетой
диаметром 2 см, если ее держать на расстоянии 60 см от глаза. Найдите
расстояние (в м) от наблюдателя до столба.
11.
Короткое плечо шлагбаума имеет длину 1 м, а
длинное плечо – 4 м. На какую высоту поднимается конец длинного плеча, когда
конец короткого плеча опускается на 0,5 м?
12.
Короткое плечо шлагбаума имеет длину 1 м, а
длинное плечо – 3 м. На какую высоту опускается конец короткого плеча, когда конец длинного плеча поднимается на 1,5 м?
Ответ дайте в метрах.
13.
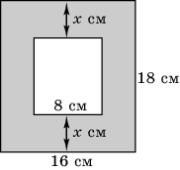
Какой должна быть ширина (x) прямоугольной рамки для
фотографии, указанной на рисунке, чтобы прямоугольники рамки и фотографии были подобны?
14.
Строительный кирпич весит 4 кг. Сколько
граммов весит игрушечный кирпич из того же материала, все размеры которого в
четыре раза меньше?
1.
Мальчик
прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел
600 м. Под каким углом к направлению на запад он должен идти, чтобы вернуться
домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических
функций.)
2.
Девочка
прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла
300 м. После этого она повернула на восток и прошла еще 100 м. Под каким углом
к направлению на восток она должна идти, чтобы вернуться домой? В ответе
укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
3.
Грибник,
войдя в лес, в течение двух часов шел в направлении на север, а затем с той же
скоростью в течение полутора часов – на восток. Под каким углом к направлению
на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? В ответе
укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
4.
Маятник
в виде груза, подвешенного на нитке, отклонили от положения равновесия на угол
60о. Длина AC маятника 20 см. На сколько
изменилась высота груза по сравнению с положением равновесия?
5.
Маятник
в виде груза, подвешенного на нитке, отклонили от положения равновесия на угол
60о. Длина AB маятника 20 см. Используя
таблицу тригонометрических функций, найдите расстояние CD от
груза C до прямой AB,
проходящей через начальное положение маятника.
6. Маятник AB длиной 50 см отклонили от положения равновесия на расстояние CD, равное 12 см. Используя таблицу тригонометрических функций, найдите угол, который образует новое положение AC маятника с положением равновесия AB.
7. Горная железная дорога поднимается на 1 м на каждые 30 м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
8. Человек, пройдя вверх по склону холма 1000 м, поднялся на 90 м над плоскостью основания холма. Используя таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
9.
Угол
подъема дороги равен 15о. Используя таблицу тригонометрических
функций, найдите высоту, на которую поднимется пешеход, пройдя 200 м.
10.
Пожарная лестница выдвинута на 50 м при
предельном угле подъема 72о. Используя таблицу значений
тригонометрических функций, найдите высоту, которой достиг верхний конец
лестницы, если ее нижний конец отстоит от поверхности земли на 1 м.
11.
Использую таблицу тригонометрических функций,
найдите приближенное значение угла, под которым виден столб высотой 3 м,
находящийся от наблюдателя на расстоянии 100 м. В ответе укажите целое число
градусов.
12. Телеграфный столб высотой 10 м находится на берегу реки. Верхний конец столба виден с другого берега под углом 20о к горизонту. Используя таблицу тригонометрических функций, найдите ширину реки.
13. Строение высоты 30 м бросает тень длиной 45 м. Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей. В ответе укажите приближенное значение, выражаемое целым числом градусов.
14. При высоте солнца в 28о заводская труба бросает тень длиной 76 м. Используя таблицу тригонометрических функций, найдите высоту трубы. В ответе укажите приближенное значение, выражаемое целым числом метров.
15.
Используя таблицу тригонометрических функций,
найдите угол наклона солнечных лучей, если длина тени стоящего человека в два
раза меньше его роста. В ответе укажите приближенное значение, выражаемое целым
числом градусов.
16.
Лестница имеет ступеньки, ширина которых
равна 30 см, а высота – 18 см. Используя таблицу тригонометрических функций,
найдите угол подъема лестницы. В ответе укажите приближенное значение,
выражаемое целым числом градусов.
17.
Угол подъема лестницы дачного домика равен 58о.
Используя таблицу тригонометрических функций, найдите высоту ступенек лестницы,
если ширина ступенек равна 20 см.
18.
Из некоторой точки вершина горы видна под
углом 30о. При приближении к горе на 1000 м вершина стала видна под
углом 45о. Найдите приближенную высоту горы. В ответе укажите целое
число метров.
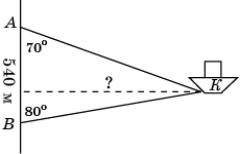
19.
Используя данные, указанные на рисунке,
найдите расстояние от корабля К до берега AB. В ответе укажите целое
число метров.
20.
С самолета радируют капитану рыболовецкого
судна, что самолет находится над косяком рыбы на высоте 1000 м. С судна
определяют, что угол, под которым виден самолет над горизонтом, равен 26о.
Используя таблицу значений тригонометрических функций, найдите расстояние от
судна до косяка рыбы. В ответе укажите приближенное значение, равное целому
числу метров.
21.
Самолет приближается к аэропорту A на
высоте 8000 м. Пилот имеет предписание производить снижение для посадки под
постоянным углом в 6о. Используя таблицу тригонометрических функций,
найдите расстояние AB от посадочной полосы до того
места, над которым самолет должен начать снижение. В ответе укажите
приближенное значение, равное целому числу метров.
22.
Расстояние от наблюдателя до башни главного
здания МГУ имени М.В. Ломоносова равно 150 м, а угол, под которым видно здание,
равен 58о. Используя таблицу значений тригонометрических функций,
найдите высоту башни. В ответе укажите приближенное значение, равное целому
числу метров.
23.
Высота башни главного здания МГУ имени М.В.
Ломоносова равна 240 м. Под каким углом видна эта башня с расстояния 200 м? В
ответе укажите приближенное значение, равное целому числу градусов.
24.
Башня главного здания МГУ имени М.В.
Ломоносова, высота которой равна 240 м, видна под углом 41о. Найдите
расстояние от наблюдателя до башни. В ответе укажите приближенное значение,
равное целому числу метров.
25.
Вершина радиомачты видна с расстояния 300 м
от ее основания под углом 10о. Используя таблицу значений
тригонометрических функций, найдите высоту радиомачты.
26.
Высота Останкинской телевизионной башни – 540
м. Используя таблицу тригонометрических функций, найдите угол в градусах, под
которым видна башня с расстояния 2000 м.
27.
Высота Останкинской телевизионной башни
равна 540 м. Под каким углом видна эта башня с расстояния 300 м? В ответе укажите
приближенное значение, равное целому числу градусов.
28.
Высота Останкинской телевизионной башни – 540
м. Используя таблицу тригонометрических функций, найдите расстояние от нее до
человека, который видит башню под углом 32о. В ответе укажите целое
число метров.
29.
Для определения высоты колонны поступили
следующим образом: отошли от ее основания на 100 м, поставили угломерный прибор
высотой 1,6 м и установили, что вершина колонны видна под углом 22
. Используя таблицу тригонометрических функций, найдите
высоту колонны.
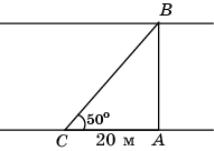
30.
Используя данные, приведенные на рисунке,
найдите ширину AB реки.
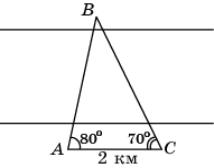
31.
Найдите расстояние между населенными пунктами
A и B, расположенными на разных
берегах реки, если расстояние между пунктами A и C, расположенными
на одном берегу этой реки, равно 2 км, угол CAB равен 80о, угол ACB равен 70о. В
ответе укажите целое число метров.
32.
Используя данные, указанные на рисунке,
найдите ширину AB озера. В ответе укажите
целое число метров.
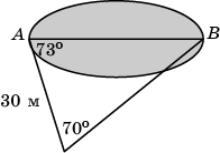
33.
Используя данные, указанные на рисунке,
найдите расстояние между населенными пунктами A и B,
расположенными на разных берегах озера. В ответе укажите целое число метров.
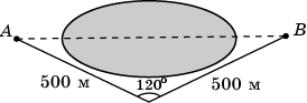
34.
Подводная лодка, находясь впереди корабля,
погрузилась в воду и пошла в направлении, перпендикулярном направлению на
корабль со скоростью 30 км/ч. Под каким углом к направлению хода подводной
лодки должен идти корабль со скоростью 60 км/ч, чтобы в некоторой точке пройти
над подводной лодкой? Ответ укажите в градусах.
35.
Пешеход пошел по направлению, составляющему
угол 35о с направлением дороги. На сколько метров он удалится от
дороги, пройдя 1000 м?
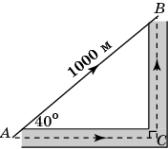
36.
Используя
данные, указанные на рисунке, выясните, на сколько метров путь из A в B по
прямой короче пути из A в B по
дороге. В ответе укажите целое число метров.
37.
Пирамида Хеопса имеет форму правильной
четырехугольной пирамиды, сторона основания которой равна 230 м, а высота около
138 м. Найдите угол наклона ее боковой грани к плоскости основания. В ответе
укажите целое число градусов.
38.
Используя таблицу значений тригонометрических
функций, найдите приближенное значение числа 
, принимая за длину окружности периметр описанного около нее
правильного шестиугольника.
39.
Используя таблицу значений тригонометрических
функций, найдите приближенное значение числа 
, принимая за длину окружности периметр вписанного в нее
правильного десятиугольника.
40.
Используя таблицу значений тригонометрических
функций, найдите приближенное значение числа 
, принимая за длину окружности периметр описанного около нее
правильного десятиугольника.
41.
Ширина футбольных ворот равна 8 ярдам.
Расстояние от 11-метровой отметки до линии ворот равно 12 ярдам. Найдите угол,
под которым видны ворота с 11-метровой отметки. В ответе укажите целое число
градусов.
42.
Ширина футбольных ворот равна 8 ярдам. Для
разметки вратарской площадки на расстоянии 6 ярдов от каждой стойки ворот под
прямым углом к линии ворот вглубь поля проводятся два отрезка длиной 6 ярдов
каждый. Концы этих отрезков соединяются отрезком, параллельным линии ворот.
Найдите угол, под которым видны ворота с угла вратарской площадки. В ответе
укажите целое число градусов.
43.
Ширина футбольных ворот равна 8 ярдам. Для
разметки штрафной площади на футбольном поле на расстоянии 18 ярдов от каждой
стойки ворот под прямым углом к линии ворот вглубь поля проводятся два отрезка,
длиной 18 ярдов каждый. Концы этих отрезков соединяются отрезком, параллельным
линии ворот. Найдите угол, под которым видны ворота с угла штрафной площади. В
ответе укажите целое число градусов.
44.
Поверхность Земли имеет форму сферы, длина
большой окружности которой приближенно равна 40000 км. Используя таблицу
значений тригонометрических функций, найдите длину окружности параллели, на
которой находится г. Москва, считая широту
Москвы, равной 56о. В ответе укажите приближенное значение,
равное целому числу километров.
45.
Поверхность Земли имеет форму сферы, длина
большой окружности которой приближенно равна 40000 км. Длина окружности
параллели, на которой находится г. Санкт-Петербург, приближенно равна 20000 км.
Найдите широту Санкт-Петербурга в градусах.
6. Площадь
1.
Площадь
земельного участка, имеющего форму прямоугольника, равна 9 га, ширина участка равна
150 м. Найдите длину этого участка.
2.
Найдите
периметр прямоугольного участка земли, площадь которого равна 800 м2
и одна сторона в 2 раза больше другой.
3. Футбольное поле имеет форму прямоугольника, длина которого в 1,5 раза больше ширины. Площадь футбольного поля равна 7350 м2. Найдите его ширину.
4. Ширина футбольных ворот равна 8 ярдам, высота – 8 футам. Найдите площадь футбольных ворот в квадратных футах (один ярд составляет три фута).
5. Для разметки вратарской площадки на футбольном поле на расстоянии 6 ярдов от каждой стойки ворот под прямым углом к линии ворот вглубь поля проводятся два отрезка длиной 6 ярдов. Концы этих отрезков соединяются отрезком, параллельным линии ворот. Найдите площадь вратарской площадки в квадратных футах, учитывая, что ширина ворот равна 8 ярдам (один ярд составляет три фута).
6. Для разметки штрафной площади на футбольном поле на расстоянии 18 ярдов от каждой стойки ворот под прямым углом к линии ворот вглубь поля проводятся два отрезка длиной 18 ярдов. Концы этих отрезков соединяются отрезком, параллельным линии ворот. Найдите приближенную площадь штрафной площади в квадратных метрах, учитывая, что ширина ворот равна 8 ярдам (один ярд приближенно равен 0,9 м). В ответе укажите целое число квадратных метров.
7. Ширина хоккейных ворот равна 6 футам, высота – 4 футам. Найдите приближенную площадь ворот в квадратных метрах с точностью до двух знаков после запятой. (Один фут равен 30,5 см.)
8.
Хоккейная площадка имеет форму прямоугольника размером 200х85
(футов) с углами, закругленными по дугам окружностей радиуса 28 футов. Найдите
примерную площадь хоккейной площадки в квадратных футах. (Примите 
.)
9. Пол комнаты, имеющей форму прямоугольника со сторонами 5 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 30 см. Сколько потребуется таких дощечек?
10.
Сколько потребуется кафельных плиток
квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму
прямоугольника со сторонами 3 м и 2,7 м?
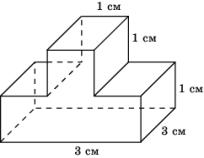
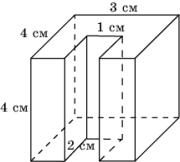
11. Найдите площадь стены заводского здания, изображенной на рисунке.
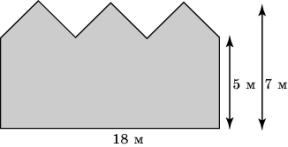
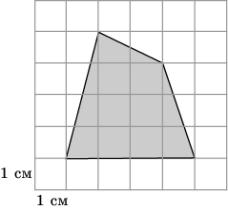
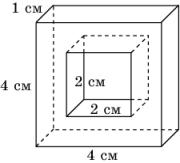
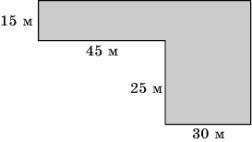
12. Найдите площадь земельного участка, изображенного на рисунке.
13.
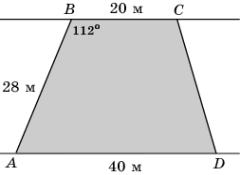
Участок между двумя параллельными улицами
имеет вид четырехугольника ABCD
(AD||BC) AB=28 м, BC=20 м, AD=40 м, 
B=112
. Найдите площадь
этого участка. В ответе укажите приближенное значение, равное целому числу
квадратных метров.
14.
Площадь участка земли равна 1200 м2.
Чему равна его площадь (в дм2) на плане, если масштаб равен 1:100?
15.
Площадь плана участка земли равна 3,75 дм2,
масштаб плана 1:200. Чему равна площадь самого участка (в м2)?
16.
Две трубы, диаметры которых равны 10 см и 24
см, требуется заменить одной, не изменяя их пропускной способности. Каким
должен быть диаметр новой трубы?
17.
Дерево имеет в обхвате 120 см. Найдите
примерную площадь поперечного сечения (в см2), имеющего форму круга.
(Примите 
.)
18.
Бумажная лента плотно намотана на катушку, внутренний
диаметр которой равен 20 см. Толщина бумаги равна 0,5 мм, а толщина намотанного
рулона – 30 см. Найдите длину бумажной ленты. Ответ дайте в метрах. (Примите 
.)
19.
Из квадратного листа жести со стороной 20 см
вырезали круг наибольшего диаметра. Какой примерный процент площади листа жести
составляет площадь обрезков? (Примите 
.)
20.
Зрачок человеческого глаза, имеющий форму круга,
может изменять свой диаметр в зависимости от освещения от 1,5 мм до 7,5 мм. Во
сколько раз при этом увеличивается площадь поверхности зрачка?
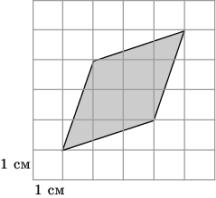
21.
Пол требуется покрыть паркетом из белых и
черных плиток, имеющих форму правильных шестиугольников. Фрагмент паркета
показан на рисунке. Во сколько раз белых плиток паркета больше чем черных?
22.
Пол требуется покрыть паркетом из
восьмиугольных и квадратных плиток. Фрагмент паркета показан на рисунке.
Найдите отношение числа квадратных плиток к числу восьмиугольных.
29.
Найдите площадь поверхности детали,
изображенной на рисунке, составленной из двух частей цилиндров. (Примите 
.)
31.
Какого наименьшего периметра может быть
прямоугольная площадка площади 100 м2?
7. Объем
1.
Сколько
коробок в форме прямоугольного параллелепипеда размерами 30х40х50 (см) можно
поместить в кузов машины размерами 2х3х1,5 (м)?
2.
Сколько
досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной
балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см x 40 см?
3.
Размеры
кирпича 25х12х6,5 (см). Найдите вес одного кирпича в граммах, если объемный вес
кирпича равен 1700 кг/м3.
4.
Какова должна быть площадь кабинета высотой 3,5
м для класса в 28 человек, если на каждого ученика нужно 7,5 м3
воздуха?
5.
Прямолинейный
участок дороги шириной 10 м и длиной 100 м требуется покрыть асфальтом толщиной
5 см. Сколько потребуется машин асфальта, если объемный вес асфальта равен 2,4
т/м3, а грузоподъемность одной машины – 5 тонн?
6.
Пирамида Хеопса имеет форму правильной
четырехугольной пирамиды, сторона основания которой равна 230 м, а высота около
138 м. Найдите ее объем в кубических метрах.
7.
В
цилиндрический сосуд, в котором находится 6 дм3 воды, опущена
деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен
объем детали в кубических дециметрах?
8.
Воду, находящуюся в цилиндрическом сосуде на
уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На
какой высоте будет находиться уровень воды во втором сосуде?
9.
Одна цилиндрическая кружка вдвое выше второй,
зато вторая в полтора раза шире. Найдите отношение объема второй кружки к
объему первой.
10.
Воду, заполняющую всю коническую колбу
высотой 12 см, перелили в цилиндрический сосуд, радиус основания которого равен
радиусу окружности конической колбы. На какой высоте от основания
цилиндрического сосуда будет находиться поверхность воды?
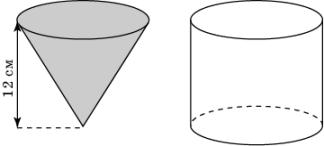
11.
Медный прямоугольный параллелепипед, ребра
которого равны 20 см, 20 см и 10 см, переплавлен в шар. Найдите радиус шара.
(Примите 
.)
16.
Чугунная труба имеет длину 2 м и внешний
диаметр 20 см. Толщина стенок трубы равна 2 см. Найдите вес трубы, если
удельный вес чугуна примерно равен 7,5 г/см3. Ответ дайте в
килограммах. (Примите 
.)
17.
Какой объем краски потребуется, чтобы
окрасить внешнюю поверхность цилиндрической трубы диаметра 1 м и длины 10 м
слоем краски в 1 мм? Ответ дайте в кубических дециметрах. (Примите 
.)
18.
Какой объем краски потребуется, чтобы
окрасить поверхность шара радиуса 1 м слоем краски в 0,5 мм? Ответ дайте в
кубических дециметрах. (Примите 
.)
24.
Найдите объем детали, изображенной на
рисунке, составленной из двух частей цилиндров. (Примите 
).
25.
Найдите объем детали, изображенной на
рисунке, вырезанной из цилиндра. (Примите 
.)
Ответы
1.
Расстояния. Теорема Пифагора
1. 33. 2. 25. 3.
1000. 4. 500. 5. 2,5. 6. 50. 7. 500. 8. 12. 9.
5. 10. 10. 11. 65. 12. 1,5. 13. 13. 14. 48. 15.
10. 16. 2,8. 17. 6. 18. 89. 19. 8,6. 20. 6.
2. Углы
1. 20. 2. 20. 3.
5. 4. 30. 5. 150. 6. 60. 7. 10. 8. 18. 9.
3. 10. 135. 11. 36. 12. 120. 13. 6. 14. 45. 15.
80. 16. 108. 17. 25. 18. 6. 19. 1,5. 20. 45.
3. Окружность
1. 3. 2. 3. 3.
3. 4. 375. 5. 64,8. 6. 12. 7. 15. 8. 21. 9.
35. 10. 3. 11. 1000. 12. 540. 13. 6. 14.
200. 15. 12. 16. 1333. 17. 70. 18. 160. 19.
160. 20. 10. 21. 78. 22. 42. 23. 1. 24. 72. 25.
510. 26. 960. 27. 408000. 28. 156000000. 29. 4. 30.
12.
4.
Подобие
1. 100. 2. 5. 3. 10. 4.
30. 5. 17. 6. 3. 7. 144. 8. 6. 9. 18. 10.
450. 11. 2. 12. 0,5. 13. 4,5. 14. 62,5. 15.
320. 16. 150. 17. 110. 18. 27,5. 19. 400. 20.
154000000.
1. 37. 2. 37. 3.
37. 4. 10. 5. 17,4. 6. 14. 7. 2. 8. 5. 9.
52. 10. 48,5. 11. 2. 12. 27,8. 13. 34. 14.
40. 15. 64. 16. 31. 17. 32. 18. 1381. 19.
1000. 20. 2020. 21. 76080. 22. 240. 23. 50. 24.
276. 25. 54. 26. 15. 27. 61. 28. 864. 29.
41,6. 30. 23,8. 31. 3760. 32. 47. 33. 870. 34.
30. 35. 570. 36. 410. 37. 50. 38. 3,48. 39.
3,1. 40. 3,2. 41. 37. 42. 22. 43. 10. 44.
22400. 45. 60.
6. Площадь
1. 600. 2. 120. 3.
70. 4. 192. 5. 1080. 6. 642. 7. 2,23. 8.
16216. 9. 2000. 10. 360. 11. 108. 12. 1875. 13. 781.
14. 12. 15. 1500. 16. 26. 17. 1200. 18. 300.
19. 25. 20. 25. 21. 2. 22. 1. 23. 420000. 24.
320000. 25. 38. 26. 92. 27. 48. 28. 78. 29.
1050. 30. 68. 31. 40. 32. 160000.
7. Объем
1. 150. 2. 90. 3.
3315. 4. 60. 5. 24. 6. 2433400. 7. 3. 8. 3. 9.
1,125. 10. 4. 11. 10. 12. 27. 13. 6. 14. 26.
15. 960. 16. 162. 17. 30. 18. 6. 19. 9. 20.
12. 21. 40. 22. 12. 23. 144. 24. 2250. 25.
3000. 26. 64000000.
Таблица приближенных
значений тригонометрических функций
A
|
sin A |
tg A |
A |
sin A |
tg A |
A |
sin A |
tg A |
|
30' |
0,0087 |
0,0087 |
30о |
0,50 |
0,58 |
60о |
0,87 |
1,73 |
|
1о |
0,0175 |
0,0175 |
31о |
0,52 |
0,60 |
61о |
0,87 |
1,80 |
|
2о |
0,035 |
0,035 |
32о |
0,53 |
0,62 |
62о |
0,88 |
1,88 |
|
3о |
0,05 |
0,05 |
33о |
0,54 |
0,65 |
63о |
0,89 |
1,96 |
|
4о |
0,07 |
0,07 |
34о |
0,56 |
0,68 |
64о |
0,90 |
2,02 |
|
5о |
0,09 |
0,09 |
35о |
0,57 |
0,70 |
65о |
0,91 |
2,15 |
|
6о |
0,10 |
0,11 |
36о |
0,59 |
0,73 |
66о |
0,91 |
2,25 |
|
7о |
0,12 |
0,12 |
37о |
0,60 |
0,75 |
67о |
0,92 |
2,36 |
|
8о |
0,14 |
0,14 |
38о |
0,62 |
0,78 |
68о |
0,93 |
2,48 |
|
9о |
0,16 |
0,16 |
39о |
0,63 |
0,81 |
69о |
0,93 |
2,61 |
|
10о |
0,17 |
0,18 |
40о |
0,64 |
0,84 |
70о |
0,94 |
2,78 |
|
11о |
0,19 |
0,19 |
41о |
0,66 |
0,87 |
71о |
0,95 |
2,90 |
|
12о |
0,21 |
0,21 |
42о |
0,67 |
0,9 |
72о |
0,95 |
3,08 |
|
13о |
0,23 |
0,23 |
43о |
0,68 |
0,93 |
73о |
0,96 |
3,27 |
|
14о |
0,24 |
0,25 |
44о |
0,69 |
0,97 |
74о |
0,96 |
3,49 |
|
15о |
0,26 |
0,27 |
45о |
0,71 |
1,00 |
75о |
0,97 |
3,73 |
|
16о |
0,28 |
0,29 |
46о |
0,72 |
1,04 |
76о |
0,97 |
4,01 |
|
17о |
0,29 |
0,31 |
47о |
0,73 |
1,07 |
77о |
0,97 |
4,33 |
|
18о |
0,31 |
0,32 |
48о |
0,74 |
1,11 |
78о |
0,98 |
4,71 |
|
19о |
0,33 |
0,34 |
49о |
0,75 |
1,15 |
79о |
0,98 |
5,15 |
|
20о |
0,34 |
0,36 |
50о |
0,77 |
1,19 |
80о |
0,98 |
5,67 |
|
21о |
0,36 |
0,38 |
51о |
0,78 |
1,23 |
81о |
0,99 |
6,31 |
|
22о |
0,37 |
0,40 |
52о |
0,79 |
1,28 |
82о |
0,99 |
7,12 |
|
23о |
0,39 |
0,42 |
53о |
0,80 |
1,33 |
83о |
0,992 |
8,14 |
|
24о |
0,41 |
0,45 |
54о |
0,81 |
1,38 |
84о |
0,994 |
9,51 |
|
25о |
0,42 |
0,47 |
55о |
0,82 |
1,43 |
85о |
0,996 |
11,43 |
|
26о |
0,44 |
0,49 |
56о |
0,83 |
1,48 |
86о |
0,998 |
14,30 |
|
27о |
0,45 |
0,51 |
57о |
0,84 |
1,54 |
87о |
0,999 |
19,08 |
|
28о |
0,47 |
0,53 |
58о |
0,85 |
1,60 |
88о |
1,00 |
28,64 |
|
29о |
0,48 |
0,55 |
59о |
0,86 |
1,66 |
89о |
1,00 |
57,29 |
