ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ.

Проблема нахождения объемов пространственных фигур с древних вре­мен привлекала к себе внимание ученых. Вычислением объемов простейших пространственных фигур занимались Демокрит, Ев­докс (406-355 гг. до н. э.), Архимед. В средние века нахождением объемов пространственных фигур занимались И. Кеплер, Б. Кавальери (1598-1647), П. Ферма (1601-1665) и др. Появ­ление интегрального исчисления в конце XVII века в работах И. Ньютона (1643-1727) и Г. Лейбница (1646-1716) дало мощный метод вычисления объ­емов произвольных пространственных фигур. Знакомство с этим методом происходит в курсе алгебры и начал анализа. Здесь же мы рассмотрим са­мо понятие объема, его свойства и вычисление объемов основных прост­ранственных фигур.

Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины. Напри­мер, если за единицу измерения длины принимается 1 мм, 1 см или 1 м, то за единицу измерения объема принимается куб, ребро которого равно соответственно 1 мм, 1 см или 1 м. Такой куб называется кубическим миллиметром, кубическим сантиметром или кубическим метром соответс­твенно.

Точное определение объема фигуры в пространстве дается в курсе математического анализа, и использует понятия предела или верхней и нижней граней. Здесь мы ограничимся тем, что объем это число V, показывающее сколько раз единица измерения объема и ее части укладываются в данной фигуре.

Это число может быть натуральным, рациональным или даже иррациональным.

Ясно, что объем фигуры зависит от единицы измерения. Поэтому, на практике, после этого числа ука­зывают единицу измерения объема. Например, V мм³, V см³, V м³.

Для объемов пространственных фигур справедливы свойства, анало­гичные свойствам площадей плоских фигур, а именно:

1. Объем фигуры в пространстве является неотрицательным числом.

2. Равные фигуры имеют равные объемы.

3. Если фигура Ф составлена из двух неперекрывающихся фигур Ф₁ и Ф₂, то объем фигу­ры Ф равен сумме объемов фигур Ф₁ и Ф₂, т.е.

V(Ф)=V(Ф₁)+V(Ф₂).

Две фигуры, имеющие равные объемы, называются  равновеликими.

Для нахождения объемов фигур удобно объединить некоторые фигуры в один класс. С этой целью дадим общее определение цилиндра.

Пусть α и π - две параллельные плоскости, l - пересекающая эти плоскости прямая; F – фигура на одной из этих плоскостей, F’ – ее параллельная проекция на другую плоскость в направлении прямой l (рис. 1, а). Отрез­ки, соединяющие точки фигуры F с их проекциями, образуют фигуру в пространстве, которую мы будем называть цилиндром. Фигуры F и F’ называются ос­нованиями цилиндра. Расстояние между плоскостями оснований называют высотой цилиндра.

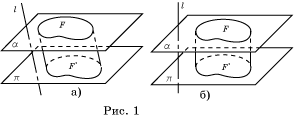
В случае, если в определении цилиндра вместо параллельной проекции берется ортогональная, т. е. прямая l перпендикулярна плоскостям α и π, то цилиндр называется прямым (рис. 1, б). В противном случае цилиндр называется наклонным.

Заметим, что частным случаем цилиндра является призма.

В случае, если основание F цилиндра является кругом, то цилиндр называется круговым.

Ранее мы рассматривали только круговые цилиндры и называли их просто цилиндрами.

Здесь мы найдем формулу для вычисления объема прямого цилиндра, основанием которого является произвольная плоская фигура.

Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту.

Доказательство. Рассмотрим сначала случай, когда в основании цилиндра  Ф₁ квадрат со стороной, равной единице и высота которого равна h (рис. 2, а). Так как единица измерения длины укладывается в высоте h раз, то и единичный куб будет укладываться в этом цилиндре h раз и, следовательно, объем цилиндра равен h.

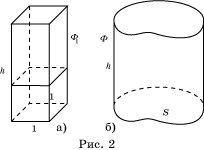
Пусть теперь Ф - прямой цилиндр, основанием которого служит фигура F, площади S, и высота которого равна h (рис. 2, б). Так как единичный квадрат укладывается в основании S раз, то и цилиндр Ф₁ будет укладываться в  цилиндре Ф S раз.

Таким образом, единица измерения объема укладывается в цилиндре Ф₁ h раз и цилиндр Ф₁ укладывается в цилиндре Ф S раз. Следовательно, единица измерения объема будет укладываться в цилиндре Ф S·h раз, т. е. имеет место формула

где S - площадь основания, h - высота цилиндра.

Поскольку частным случаем цилиндра является параллелепипед, призма и круговой цилиндр, то имеем.

Следствие 1. Объем прямоугольного параллелепипеда равен произведению трех его измерений, т. е. имеет место формула

где a, b, c – ребра параллелепипеда.

Следствие 2. Объем прямой призмы равен произведению площади ее основания на высоту, т. е. имеет место формула

 

где S – площадь основания, h – высота призмы.

Следствие 3. Объем прямого кругового цилиндра, высота которого равна h и ради­ус основания  R, вычисляется по формуле

 

Рассмотрим метод вычисления объемов пространственных фигур, предложенный итальянским математиком Бонавентурой Кавальери (1598–1647) и назван­ный впоследствии принципом Кавальери. Он заключается в следующем.

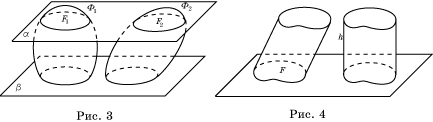
Принцип Кавальери. Если при пересечении двух фигур Ф₁ и Ф₂ в пространстве плоскостями, параллельными одной и той же плоскости, в сечениях полу­чаются фигуры F₁ и F₂ одинаковой площади (рис. 3), то объемы исходных пространственных фигур равны.

Для обоснования этого принципа представим фигуры Ф₁ и Ф₂, состав­ленными из тонких слоев одинаковой толщины, которые получаются при пересече­нии фигур Ф₁ и Ф₂ плоскостями, параллельными некоторой заданной плоскости (рис. 3). Считая слои прямыми ци­линдрами, из равенства площадей их оснований и равенства высот получа­ем, что равны и объемы соответствующих слоев. Следовательно, равны и объемы фигур Ф₁ и Ф₂, составленных из этих слоев.

Теорема. Объем наклонного цилиндра равен произведению площади его основания на высоту.

Доказательство. Для данного наклонного цилиндра с основа­нием F площади S и высотой h рассмотрим прямой цилиндр с таким же основанием и высотой. Расположим эти два цилиндра так, чтобы их основания находились на одной плоскости (рис. 4). Тогда сечения этих цилиндров плоскостями, параллельными этой плоскости, дадут фигу­ры, равные фигуре F и, следовательно, они будут иметь равные площади. По принципу Кавальери, отсюда следует равенство объемов цилиндров и, значит, для объема наклонного цилиндра имеет место формула:

где S - площадь основания, h - высота цилиндра.

Следствие 1. Объем наклонной призмы с площадью основания S и высотой h вычисляется по формуле

Следствие 2. Объем наклонного кругового цилиндра, высота которого равна h и ради­ус основания  R, вычисляется по формуле

Дадим общее определение конуса, позволяющее объединить в один класс рассмотренные ранее конусы и пирамиды.

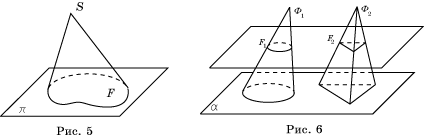
Пусть F - фигура на плоскости π, и S - точка вне этой плоскости. Отрезки, соединяющие точки фигуры F с точкой S, образуют фигуру в пространстве, которую мы будем называть конусом (рис. 5). Фигура F называется основанием конуса, точка S - вершиной конуса. Перпендикуляр, опущенный из вершины конуса на плоскость основания, называется высотой конуса.

В случае, если F является кругом, конус называется круговым. Если высота кругового конуса проходит через центр основания, то такой конус называется прямым кру­говым. Раньше мы рассматривали прямые круговые конусы и называли их просто конусами. Заметим, что частным случаем конуса в новом понимании является также пирамида.

Используя принцип Кавальери, докажем следующую теорему.

Теорема. Если два конуса имеют равные высоты и основания равной площади, то их объемы равны.

Доказательство.  Пусть конусы Ф₁ и Ф₂ имеют высоты, равные h, а основания площади S расположены в одной плоскости  (рис. 6). Проведем плоскость, параллельную плоскости , на расстоянии x от нее, 0xh. Тогда фигуры F₁ и F₂, получающиеся в сечениях конусов этой плоскостью, подобны соответствующим основаниям, и коэффициент подобия k в обоих случаях равен  (h – x):h. Следовательно, площади S₁ и S₂ фигур F₁ и F₂ соответственно выражаются формулами S₁ = k²S, S₂ = k²S и, значит, равны. Из принципа Кавальери получаем, что объемы конусов равны.

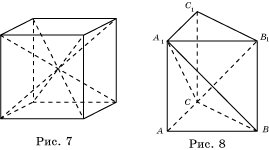
Первые упоминания о вычислении объема пирамиды найдены в папиру­сах древних вавилонян и египтян (свыше 3000 лет до н. э.). Любопытно, что они не вывели общей формулы для нахождения объема пирамиды, а вы­числяли объемы конкретных пирамид. Так им удалось найти объем правиль­ной четырехугольной пирамиды с основанием, равным единице измерения, и высотой, равной . Для этого они брали куб с ребром, равным единице измерения, и разбивали его на 6 равных правильных четырехугольных пи­рамид. Основаниями этих пирамид будут грани куба, а вершина каждой из них будет находиться в центре куба (рис. 7). Все 6 полученные пирамиды рав­ны, отсюда получаем, что объем каждой из них равен  объема куба.

Теорема. Объем пирамиды равен одной третьей произведения площади ее основания на высоту.

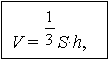
Доказательство. Рассмотрим сначала случай треугольной пирамиды. Пусть A₁ABC треугольная пирамида. Достроим ее до треугольной призмы ABCA₁B₁C₁ (рис. 8). Плоскости, проходящие через точки B, C, A₁ и C, B₁, A₁ разбивают эту призму на три пирамиды A₁ABC, A₁CBB₁ и A₁CB₁C₁ с верши­нами в точке A₁. Пирамиды A₁CBB₁ и A₁CB₁C₁ имеют равные основания CBB₁ и CB₁C₁, так как диагональ CB₁ разбивает параллелограмм CBB₁C₁ на два равных треугольника. Кроме этого,  данные пирамиды имеют общую вершину, а их основания лежат в одной плоскости. Значит, эти пирамиды имеют общую высоту. Следовательно, эти пирамиды имеют равные объемы. Рассмотрим теперь пирамиды A₁ABC и CA₁B₁C₁. Они имеют равные основания ABC и A₁B₁C₁ и равные высоты. Следовательно, они имеют равные объемы. Таким обра­зом, объемы всех трех пирамид равны. Учитывая, что объем призмы равен произведению площади основания на высоту, получим формулу объема треу­гольной пирамиды

где S - площадь основания пирамиды, h - ее высота.

Пусть теперь дана пирамида, в основании которой - многоугольник. Рассмотрим треугольную пирамиду с такой же высотой и такой же площадью основания. По теореме предыдущего параграфа объемы этих пирамид равны и, следовательно, имеет место формула

V = S·h,

где S - площадь основания пирамиды, h - ее высота.

Напомним, что конусом в пространстве мы называем фигуру, образо­ванную отрезками, соединяющими точки некоторой плоской фигуры, назы­ваемой основанием конуса, с точкой, лежащей вне плоскости основания и называемой вершиной конуса.

Теорема. Объем конуса равен одной третьей произведения площади его основания  на высоту.

Доказательство. Для данного конуса с основанием площади S и высотой h рассмотрим какую-нибудь пирамиду с теми же площадью основания и высотой (рис. 6). Тогда эти пирамида и конус имеют равные объемы. Но для объема пирамиды имеет место формула

V = S·h.

Следовательно, она имеет место и для объема произвольного конуса.

В частности, для кругового конуса, в основании которого – круг радиуса  R, и высота которого равна h, имеет место формула

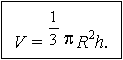
Рассмотрим вопрос о нахождении формулы объема шара.

Теорема. Объем шара радиуса R выражается формулой

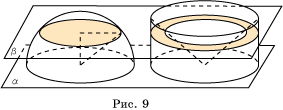
Доказательство. Пусть дан по­лушар радиуса R, основание которого расположено на плоскости . Рассмотрим цилиндр, основание которого - круг радиуса R, рас­положенный в той же плоскости , и высота которого равна R (рис. 9). В ци­линдр впишем конус, основанием которого будет верхнее основа­ние цилиндра, а вершиной - центр нижнего основания цилиндра. Докажем, что фигура, состоящая из точек цилиндра, не попавших внутрь конуса, и данный полушар имеют равные объ­емы.

Проведем плоскость β, параллельную плоскости , на расстоянии x от нее, 0xR. В сечении полушара этой плоскостью получим круг радиуса  и площади (R²-x²). В сечении другой фигуры получается кольцо, радиус внутреннего круга в котором равен x, а внешнего - R. Площадь этого кольца равна R² - x² = (R² - x²) и, следовательно, равна площади сечения полушара. Из принципа Кавальери следует, что полушар и постро­енная фигура имеют равные объемы. Вычислим этот объем. Он равен раз­ности объемов цилиндра и конуса, т.е.

V = V_ц - V_к = R²R - R²R = R³.

Объем шара вдвое больше объема полушара и, следовательно, выражается формулой

V = R³.

Найдем объем тора – фигуры, полученной вращением круга радиуса r вокруг оси, отстоящей от центра круга на расстояние d (d > r).

Воспользуемся принципом Кавальери. Пусть плоскость, перпендикулярна оси вращения a и отстоит от центра круга O на расстояние x (рис. 10).

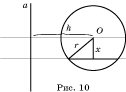
В сечении тора этой плоскостью будет кольцо площади 4d. Рассмотрим цилиндр с радиусом основания r и высотой 2d. Площадь сечения этого цилиндра плоскостью, параллельной оси и отстоящей от нее на расстояние x, также будет равна 4d. Следовательно, объем тора V равен объему цилиндра, т.е. V=2²r²d.

Пусть теперь прямая a вращается вокруг прямой c, скрещивающейся с a. Используя принцип Кавальери, найдем объем тела, ограниченного соответствующей поверхностью вращения и двумя плоскостями, перпендикулярными оси c. Угол между прямыми a и c равен ; длина их общего перпендикуляра – d; расстояния от секущих плоскостей до общего перпендикуляра прямых a и c равны c’ и c” соответственно (рис. 11).

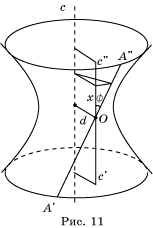
Проведем плоскость, перпендикулярную оси c на расстоянии x от точки O. Площадь соответствующего круга равна (d²+x²tg²). По принципу Кавальери, искомый объем V тела будет равен сумме объемов цилиндра с радиусом основания d и высотой c’+c” и двух конусов с радиусами оснований c’tg, c”tg и высотами c’ и c” соответственно. Таким образом,

V=d²(c’+c”)+  (c’)³tg²+ (c”)³tg².

         Используя полученную формулу, самостоятельно вычислите объем тела, полученного вращением единичного куба вокруг его диагонали.

 

         Литература

1. Энциклопедия элементарной математики. Книга V. Геометрия. - М.: Наука, 1966.

2. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.

3. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Стереометрия. – М.-Л.: Гостехиздат, 1949.

3. Глейзер Г.И. История математики в школе. IX-X классы. – М.: Просвещение, 1983, с.176.

4. Смирнова И.М., Смирнов В.А. Геометрия 10-11. Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2003.

5. Смирнова И.М., Смирнов В.А. Геометрия. Нестандартные и исследовательские задачи. Учебное пособие для 7-11 классов общеобразовательных учреждений. – М.: Мнемозина, 2004.