СИММЕТРИЯ ПРОСТРАНСТВЕННЫХ ФИГУР

    По словам известного немецкого математика Г. Вейля (1885-1955), "симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство".
    Прекрасные образы симметрии демонстрируют произведения искусства: архитектуры, живописи, скульптуры и т. д.
    Понятие симметрии фигур на плоскости рассматривалось в курсе планиметрии. В частности, определялись понятия центральной и осевой симметрии. Для пространственных фигур понятие симметрии определяется аналогичным образом.
    Рассмотрим сначала центральную симметрию.
    Точки A и A' пространства называются симметричными относительно точки O, называемой центром симметрии, если O является серединой отрезка AA'. Точка O считается симметричной сама себе.
    Преобразование пространства, при котором каждой точке A сопоставляется симметричная ей (относительно данной точки O) точка A' называется центральной симметрией. Точка O при этом называется центром симметрии.
    Две фигуры Ф и Ф' называются центрально симметричными, если существует преобразование симметрии, переводящее одну из них в другую.
    Фигура Ф называется центрально симметричной, если она центрально симметрична сама себе.
    Например, параллелепипед центрально симметричен относительно точки пересечения его диагоналей. Шар и сфера центрально симметричны относительно своих центров.
    Из правильных многогранников центрально симметричными являются куб, октаэдр, икосаэдр и додекаэдр. Тетраэдр не является центрально симметричной фигурой.
    Рассмотрим некоторые свойства центральной симметрии.
    Свойство 1. Если O₁, O₂– центры симметрии фигуры Ф, то точка O₃, симметричная O₁ относительно O₂ также является центром симметрии этой фигуры.
    Доказательство. Пусть A – точка пространства, A₂ – точка, симметричная ей, относительно O₂, A₁ – точка, симметричная A₂ относительно O₁ и A₃ – точка симметричная A₁ относительно O₂ (рис. 1).

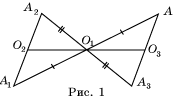
Тогда треугольники O₂O₁A₁ и O₂O₃A₃, O₂O₁A₂ и O₂O₃A равны. Следовательно, A и A₃ симметричны относительно O₃. Таким образом, симметрия относительно O₃ является композицией симметрий относительно O₂, O₁ и O₂. Следовательно, при этой симметрии фигура Ф переходит сама в себя, т.е. O₃ является центром симметрии фигуры Ф.

    Следствие. Любая фигура или не имеет центра симметрии, или имеет один центр симметрии, или имеет бесконечно много центров симметрии

Действительно, если O₁, O₂– центры симметрии фигуры Ф, то точка O₃, симметричная O₁ относительно O₂ также является центром симметрии этой фигуры. Аналогично, точка O₄ симметричная O₂ относительно O₃ также является центром симметрии фигуры Ф и т. д. Таким образом, в этом случае фигура Ф имеет бесконечно много центров симметрии.

Рассмотрим теперь понятие осевой симметрии.
    Точки A и A' пространства называются симметричными относительно прямой a, называемой осью симметрии, если прямая a проходит через середину отрезка AA' и перпендикулярна этому отрезку. Каждая точка прямой a считается симметричной сама себе.
    Преобразование пространства, при котором каждой точке A сопоставляется симметричная ей точка A' (относительно данной прямой a), называется осевой симметрией. Прямая a при этом называется осью симметрии.
    Две фигуры называются симметричными относительно прямой a, если преобразование симметрии относительно этой прямой переводит одну из них в другую.
    Фигура Ф в пространстве называется симметричной относительно прямой a, если она симметрична сама себе.
    Например, прямоугольный параллелепипед симметричен относительно прямой, проходящей через центры противоположных граней. Прямой круговой цилиндр симметричен относительно своей оси, шар и сфера симметричны относительно любых прямых, проходящих через их центры и т. д.
    Куб имеет три оси симметрии, проходящих через центры противоположных граней и шесть осей симметрии, проходящих через середины противоположных ребер.
    Тетраэдр имеет три оси симметрии, проходящих через середины противоположных ребер.
    Октаэдр имеет три оси симметрии, проходящих через противоположные вершины и шесть осей симметрии, проходящих через середины противоположных ребер.
    Икосаэдр и додекаэдр имеют по пятнадцать осей симметрии, проходящих через середины противоположных ребер.
    Свойство 3. Если a₁, a₂– оси симметрии фигуры Ф, то прямая a₃, симметричная a₁ относительно a₂ также является осью симметрии этой фигуры.

Доказательство аналогично доказательству Свойства 1.

Свойство 4. Если две пересекающиеся перпендикулярные прямые в пространстве являются осями симметрии данной фигуры Ф, то и прямая, проходящая через точку пересечения и перпендикулярная плоскости этих прямых также будет осью симметрии фигуры Ф.
    Доказательство. Рассмотрим оси координат Ox, Oy, Oz. Симметрия относительно оси Ox переводит точку фигуры Ф с координатами (x, y, z) в точку фигуры Ф с координатами (x, –y, –z). Аналогично, симметрия относительно оси Oy переводит точку фигуры Ф с координатами (x, –y, –z) в точку фигуры Ф с координатами (–x, –y, z). Таким образом, композиция этих симметрий переводит точку фигуры Ф с координатами (x, y, z) в точку фигуры Ф с координатами (–x, –y, z). Следовательно, ось Oz является осью симметрии фигуры Ф.

Следствие. Любая фигура в пространстве не может иметь четное (ненулевое) число осей симметрии.
    Действительно, зафиксируем какую-нибудь ось симметрии a. Если b – ось симметрии, не пересекает a или пересекает ее не под прямым углом, то для нее найдется еще одна ось симметрии b’, симметричная относительно a. Если же ось симметрии b пересекает a под прямым углом, то для нее найдется еще одна ось симметрии b’, проходящая через точку пересечения и перпендикулярная плоскости прямых a и b. Следовательно, кроме оси симметрии a возможно или четное или бесконечное число осей симметрии. Таким образом, общее четное (ненулевое) число осей симметрии невозможно.
    Помимо осей симметрии, определенных выше, рассматриваются также оси симметрии n-го порядка, n 2.
    Прямая a называется осью симметрии n-го порядка фигуры Ф, если при повороте фигуры Ф вокруг прямой a на угол  фигура Ф совмещается сама с собой.

Ясно, что ось симметрии 2-го порядка является просто осью симметрии.
    Например, в правильной n-угольной пирамиде прямая, проходящая через вершину и центр основания, является осью симметрии n-го порядка.
    Выясним, какие оси симметрии имеют правильные многогранники.
    Куб имеет три оси симметрии 4-го порядка, проходящих через центры противоположных граней, четыре оси симметрии 3-го порядка, проходящих через противоположные вершины и шесть осей симметрии 2-го порядка, проходящих через середины противоположных ребер.
    Тетраэдр имеет три оси симметрии второго порядка, проходящих через середины противоположных ребер.
    Икосаэдр имеет шесть осей симметрии 5-го порядка, проходящих через противоположные вершины; десять осей симметрии 3-го порядка, проходящих через центры противоположных граней и пятнадцать осей симметрии 2-го порядка, проходящих через середины противоположных ребер.
    Додекаэдр имеет шесть осей симметрии 5-го порядка, проходящих через центры противоположных граней; десять осей симметрии 3-го порядка, проходящих через противоположные вершины и пятнадцать осей симметрии 2-го порядка, проходящих через середины противоположных ребер.
    Рассмотрим понятие зеркальной симметрии.
    Точки A и A' в пространстве называются симметричными относительно плоскости , или, по-другому, зеркально симметричными, если эта плоскость проходит через середину отрезка AA' и перпендикулярна к нему. Каждая точка плоскости  считается симметричной сама себе.
    Преобразование пространства, при котором каждой точке A сопоставляется симметричная ей точка A' (относительно данной плоскости ), называется зеркальной симметрией. Плоскость  при этом называется плоскостью симметрии.
    Две фигуры называются зеркально симметричными относительно плоскости , если преобразование симметрии относительно этой плоскости переводит одну из них в другую.
    Фигура Ф в пространстве называется зеркально симметричной, если она зеркально симметрична сама себе.
    Например, прямоугольный параллелепипед зеркально симметричен относительно плоскости, проходящей через ось симметрии и параллельной одной из пар противоположных граней. Цилиндр зеркально-симметричен относительно любой плоскости, проходящей через его ось и т. д.
    Среди правильных многогранников куб и октаэдр имеют по девять плоскостей симметрии. Тетраэдр имеет шесть плоскостей симметрии. Икосаэдр и додекаэдр имеют по пятнадцать плоскостей симметрии, проходящих через пары противоположных ребер.
    Свойство 5. Композиция двух зеркальных симметрий относительно параллельных плоскостей является параллельным переносом на вектор, перпендикулярный этим плоскостям и равный по величине удвоенному расстоянию между этими плоскостями.
    Следствие. Параллельный перенос можно представить как композицию двух зеркальных симметрий.
    Свойство 6. Композиция двух зеркальных симметрий относительно плоскостей, пересекающихся по прямой является поворотом вокруг этой прямой на угол равный удвоенному двугранному углу между этими плоскостями. В частности, осевая симметрия является композицией двух зеркальных симметрий относительно перпендикулярных плоскостей.
    Следствие. Поворот можно представить как композицию двух зеркальных симметрий.
    Свойство 7. Центральная симметрия может быть представлена в виде композиции трех зеркальных симметрий.
    Докажем это свойство с помощью координатного метода. Пусть точка A в пространстве имеет координаты (x, y, z).Зеркальная симметрия относительно координатной плоскости меняет знак соответствующей координаты. Например, зеркальная симметрия относительно плоскости Oxy переводит точку с координатами (x, y, z) в точку с координатами (x, y, –z). Композиция трех зеркальных симметрий относительно координатных плоскостей переводит точку с координатами (x, y, z) в точку с координатами (–x, –y, –z), которая является центрально симметричной исходной точке A.
    Движения, переводящие фигуру Ф саму в себя, образуют группу относительно композиции. Она называется группой симметрий фигуры Ф.
    Найдем порядок группы симметрий куба.
    Ясно, что любое движение, переводящее куб в себя, оставляет центр куба на месте, переводит центры граней в центры граней, середины ребер в середины ребер и вершины в вершины.
    Таким образом, для задания движения куба достаточно определить, куда переходит центр грани, середина ребра этой грани и вершина ребра.
    Рассмотрим разбиение куба на тетраэдры, вершинами каждого из которых являются центр куба, центр грани, середина ребра этой грани и вершина ребра. Таких тетраэдров 48. Поскольку движение полностью определяется тем, в какой из тетраэдров переводится данный тетраэдр, то порядок группы симметрий куба будет равен 48.
    Аналогичным образом находятся порядки групп симметрий тетраэдра, октаэдра, икосаэдра и додекаэдра.
    Найдем группу симметрий единичной окружности S¹. Эта группа обозначается O(2). Она является бесконечной топологической группой. Представим единичную окружность как группу комплексных чисел по модулю равных единице. Имеет место естественный эпиморфизм p:O(2) --> S¹, сопоставляющий элементу u группы O(2) элемент u(1) в S¹. Ядром этого отображения является группа Z₂, порожденная симметрией единичной окружности относительно оси Ox. Следовательно, O(2)/Z₂S¹. Более того, если не учитывать групповую структуру, то имеет место гомеоморфизм O(2) и прямого произведения S¹ и Z₂.
    Аналогично, группа симметрий двумерной сферы S² обозначается O(3), и для нее имеет место изоморфизм O(3)/O(2) S².
    Группы симметрий n-мерных сфер играют важную роль в современных разделах топологии: теории многообразий, теории расслоенных пространств и др.
    Одним из самых ярких проявлений симметрии в природе являются кристаллы. Свойства кристаллов определяются особенностями их геометрического строения, в частности, симметричным расположением атомов в кристаллической решетке. Внешние формы кристаллов являются следствием их внутренней симметрии.
    Первые, еще смутные предположения о том, что атомы в кристаллах расположены правильным, закономерным, симметричным строем, высказывались в трудах различных естествоиспытателей уже в те времена, когда само понятие атома было неясным и не было никаких экспериментальных доказательств атомного строения вещества. Симметричная внешняя форма кристаллов невольно наводила на мысль о том, что внутреннее строение кристаллов должно быть симметричным и закономерным. Законы симметрии внешней формы кристаллов были полностью установлены в середине XIX века, а к концу этого века были четко и точно выведены законы симметрии, которым подчинены атомные постройки в кристаллах.
    Основоположником математической теории строения кристаллов является выдающийся российский математик и кристаллограф - Евграф Степанович Федоров (1853-1919). Математика, химия, геология, минералогия, петрография, горное дело - в каждую из этих областей внес Е.С.Федоров немалый вклад. В 1890 году он строго математически вывел все возможные геометрические законы сочетания элементов симметрии в кристаллических структурах, иначе говоря, симметрии расположения частиц внутри кристаллов. Оказалось, что число таких законов ограничено. Федоров показал, что имеется 230 пространственных групп симметрии, которые впоследствии, в честь ученого, были названы федоровскими. Это был исполинский труд, предпринятый за 10 лет до открытия рентгеновских лучей, за 27 лет до того, как с их помощью доказали существование самой кристаллической решетки. Существование 230 федоровских групп является одним из важнейших геометрических законов современной структурной кристаллографии. "Гигантский научный подвиг Е.С. Федорова, сумевшего подвести под единую геометрическую схему весь природный "хаос" бесчисленных кристаллообразований, и сейчас вызывает восхищение. Это открытие сродни открытию периодической таблицы Д.И. Менделеева."Царство кристаллов" является незыблемым памятником и конечной вершиной классической федоровской кристаллографии", - сказал академик А.В. Шубников.

    Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – 3-е изд. – М.: Учпедгиз, 1958.
2. Вейль Г. Симметрия. – М.: Наука, 1968.
3. Вигнер Е. Этюды о симметрии. – М.: Мир, 1971.
4. Гарднер М. Этот правый, левый мир. – М.: Мир, 1967.
5. Гильде В. Зеркальный мир. – М.: Мир, 1982.
6. Компанеец А.С. Симметрия в микро- и макромире. – М.: Наука, 1978.
7. Парамонова И.М. Симметрия в математике. – М.: МЦНМО, 2000.
8. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гос изд. технико-теоретич. литературы, 1949.
9. Сонин А.С. Постижение совершенства (симметрия, асимметрия, диссимметрия, антисимметрия). – М.: Знание, 1987.
10. Тарасов Л.В. Этот удивительно симметричный мир. – М.: Просвещение, 1982.
11. Узоры симметрии. – М.: Мир, 1980.
12. Шафрановский И.И. Симметрия в природе. – 2-е изд. – Л.; 1985.
13. Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. – М.: Наука, 1972.