ПОЛУПРАВИЛЬНЫЕ И ЗВЕЗДЧАТЫЕ МНОГОГРАННИКИ

    Если в определении правильного многогранника допустить, чтобы гранями многогранника могли быть различные правильные многоугольники, то получим многогранники, которые называются полуправильными (равноугольно полуправильными).
    Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон) и все многогранные углы равны.
    Как и в случае правильных многогранников, вместо второго условия (равенства многогранных углов) в определении полуправильного многогранника можно было бы сформулировать более слабое условие, а именно: в каждой вершине многогранника сходится одинаковое число ребер.
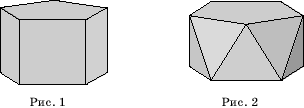
    К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны. Например, правильная пятиугольная призма на рисунке 1 имеет своими гранями два правильных шестиугольника - основания призмы и шесть квадратов, образующих боковую поверхность призмы. К полуправильным многогранникам относятся и так называемые антипризмы. На рисунке 2 мы видим пятиугольную антипризму, полученную из пятиугольной призмы поворотом одного из оснований относительно другого на угол 36. Каждая вершина верхнего и нижнего оснований соединена с двумя ближайшими вершинами другого основания.

    Кроме этих двух бесконечных серий полуправильных многогранников имеется еще 13 полуправильных многогранников которые впервые открыл и описал Архимед - это тела Архимеда.
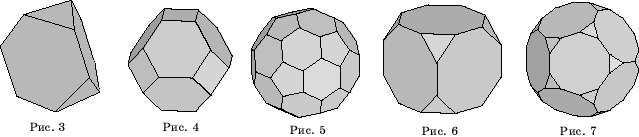
    Самые простые из них получаются из правильных многогранников операцией "усечения", состоящей в отсечении плоскостями углов многогранника. Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий восемь граней (рис. 3). Из них четыре - правильные шестиугольники и четыре - правильные треугольники. В каждой вершине этого многогранника сходятся три ребра.
    Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр (рис. 4) и усеченный икосаэдр (рис. 5). Обратите внимание на то, что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра. Из куба и додекаэдра также можно получить усеченный куб (рис. 6) и усеченный додекаэдр (рис. 7).

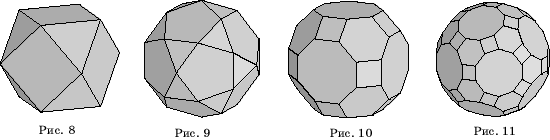
    Для того, чтобы получить еще один полуправильный многогранник, проведем в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины. В результате получим полуправильный многогранник, который называется кубооктаэдром (рис. 8). Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название - кубооктаэдр.
    Аналогично, если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром (рис. 9). У него двадцать граней - правильные треугольники и двенадцать граней - правильные пятиугольники, т.е. все грани икосаэдра и додекаэдра.

    Заметим, что повторное применение операции усечения к полученным полуправильным многогранникам уже не дает полуправильных многогранников. Дело в том, что многогранные углы данных многогранников не являются правильными. Поэтому многоугольники, получающиеся в сечении этих углов, также не будут правильными.
    Например, если операцию усечения применить к кубооктаэдру, то в сечениях многогранных углов получим прямоугольники, но не квадраты. Тем не менее существует полуправильный многогранник (рис. 10), похожий на усеченный кубооктаэдр, гранями которого являются правильные восьмиугольники, шестиугольники и квадраты. Этот многогранник называется усеченным кубооктаэдром, хотя он не получается из кубооктаэдра операцией усечения.
    Аналогично, если операцию усечения применить к икосододекаэдру, то в сечениях многогранных углов получим прямоугольники, но не квадраты. Тем не менее существует полуправильный многогранник (рис. 11), похожий на усеченный икосододекаэдр, гранями которого являются правильные десятиегольники, шестиугольники и квадраты. Этот многогранник называется усеченным икосододекаэдром, хотя он не получается из икосододекаэдра операцией усечения.
    Мы рассмотрели 9 из 13 описанных Архимедом полуправильных многогранников. Четыре оставшихся - многогранники более сложного типа.
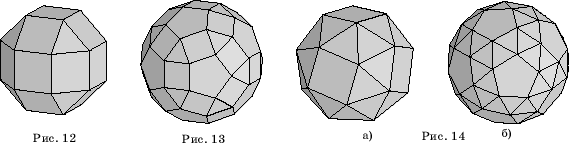
    На рисунке 12 мы видим ромбокубооктаэдр. Его поверхность состоит из граней куба и октаэдра, к которым добавлены еще 12 квадратов.
    На рисунке 13 изображен ромбоикосододекаэдр, поверхность которого состоит из граней икосаэдра, додекаэдра и еще 30 квадратов. На рисунках 14, а, б представлены соответственно так называемые плосконосый (иногда называют курносый) куб и плосконосый (курносый) додекаэдр, поверхности которых состоят из граней куба или додекаэдра, окруженных правильными треугольниками.

    Как видим, каждая поверхность этих многогранников состоит из двух или трех типов граней: квадраты, треугольники, пятиугольники и треугольники, квадраты, пятиугольники и треугольники. Модели этих многогранников будут особенно привлекательны, если при их изготовлении грани каждого типа раскрасить в свой особый цвет.
    Полуправильные многогранники называют также равноугольно полуправильными многогранниками, из-за того, что все их многогранные углы равны. Рассмотрим многогранники, двойственные к полуправильным многогранникам. Их центры граней являются вершинами полуправильных многогранников. Они образуют класс, так называемых равногранно полуправильных многогранников. У этих многогранников равны все грани, которые, однако, не являются правильными многоугольниками, и равны все двугранные углы.
    На рисунках 15, а-в показаны многогранники, двойственные к усеченному тетраэдру, усеченному кубу и усеченному октаэдру.

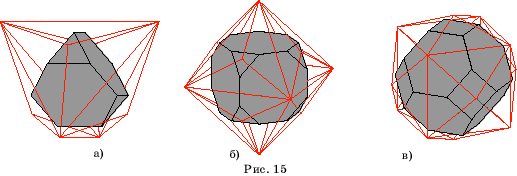
    На рисунках 15, г-н показаны многогранники, двойственные к остальным полуправильным многогранникам.

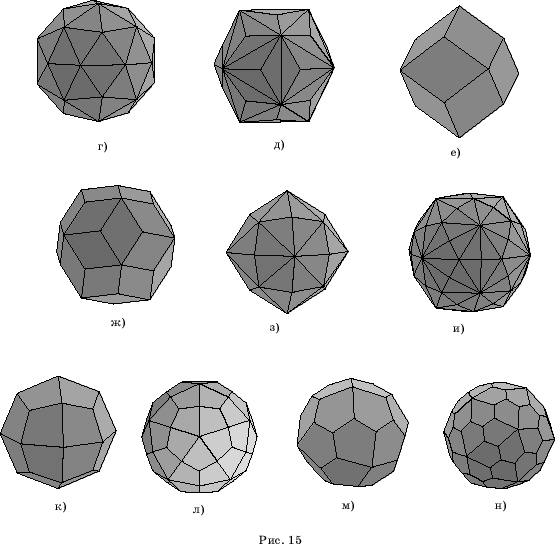
    Многогранник на рисунке 15, е называется ромбододекаэдром. Его гранями являются 12 ромбов. Форму этого многогранника имеет кристалл граната.
    Кроме правильных и полуправильных многогранников красивые формы имеют так называемые правильные звездчатые многогранники. Они получаются из правильных многогранников продолжением граней или ребер аналогично тому, как правильные звездчатые многоугольники получаются продолжением сторон правильных многоугольников.
    Первые два правильных звездчатых многогранника были открыты И. Кеплером (1571-1630), а два других почти 200 лет спустя построил французский математик и механик Л. Пуансо (1777-1859). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.
    В работе "О многоугольниках и многогранниках" (1810) Пуансо описал четыре правильных звездчатых многогранника, но вопрос о существовании других таких многогранников оставался открытым. Ответ на него был дан год спустя, в 1811 году, французским математиком О. Коши (1789-1857). В работе "Исследование о многогранниках он доказал, что других правильных звездчатых многогранников не существует.
    Рассмотрим вопрос о том, из каких правильных многогранников можно получить правильные звездчатые многогранники. Из тетраэдра, куба и октаэдра правильные звездчатые многогранники не получаются. Возьмем додекаэдр. Продолжение его ребер приводит к замене каждой грани звездчатым правильным пятиугольником (рис. 16,а), и в результате возникает многогранник, который называется малым звездчатым додекаэдром (рис. 16,б).
    При продолжении граней додекаэдра возникают две возможности. Во-первых, если рассматривать правильные пятиугольники, то получится так называемый большой додекаэдр (рис. 17). Если же, во-вторых, в качестве граней рассматривать звездчатые пятиугольники, то получается большой звездчатый додекаэдр (рис. 18).
    Икосаэдр имеет одну звездчатую форму. При продолжении граней правильного икосаэдра получается большой икосаэдр (рис. 19).

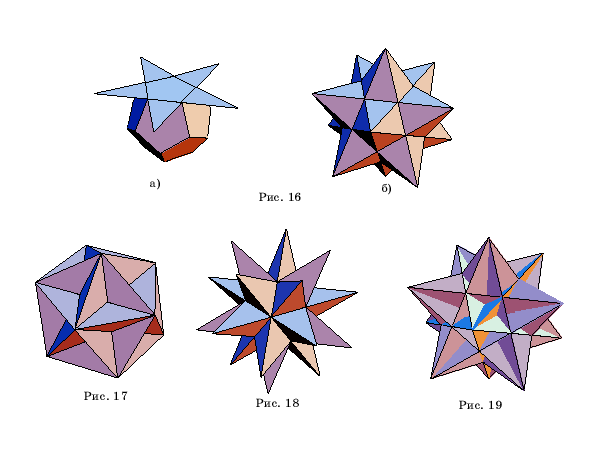
    Таким образом, существуют 4 типа правильных звездчатых многогранников.
    Кроме правильных звездчатых многогранников существуют и другие звездчатые формы, получающиеся продолжением граней правильных и полуправильных многогранников.
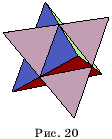
       На рисунке 20 изображен многогранник, называемый звездчатым октаэдром. Он был открыт Леонардо да Винчи, затем спустя почти сто лет переоткрыт И. Кеплером и назван им "Stella octangula" - звезда восьмиу-гольная. Этот многогранник можно получить продолжением граней октаэдра или как объединение двух тетраэдров.

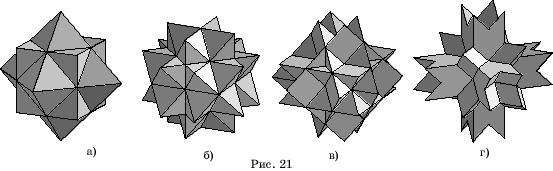
    Продолжения граней кубооктаэдра приводят к четырем звездчатым многогранникам. Первый из них (рис. 21, а) получается достраиванием на гранях кубооктаэдра пирамид и представляет собой соединение куба и октаэдра.
    Следующая звездчатая форма кубооктаэдра представлена на рисунке 21, б. Она образована из соединения куба и октаэдра добавлением 24 бипирамид.
    Третья звездчатая форма кубооктаэдра (рис. 21, в) представляет собой соединение шести четырехугольных пирамид, основаниями которых служат квадраты.
    Последняя звездчатая форма кубооктаэдра (рис. 21, г) является соединением звезды Кеплера и трех правильных четырехугольных призм, общей частью которых служит исходный куб.
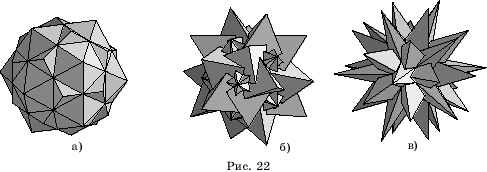
    Икосододекаэдр имеет 19 звездчатых форм, некоторые из которых представлены на рисунке 22.

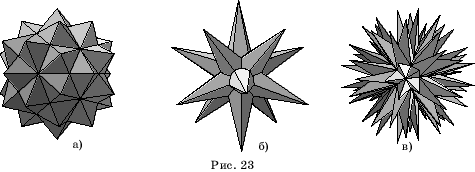
    Наконец, икосаэдр имеет 59 звездчатых форм, некоторые из которых представлены на рисунке 23.

    Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре.
   Многие формы звездчатых многогранников подсказывает сама природа в виде кристаллов. Снежинки - это тоже звездчатые многогранники (рис 24). С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

    Литература
1. Александров А.Д. Выпуклые многогранники. – М., Л.: Гос. изд. техн.-теорет. литературы, 1950.
2. Гамаюнов В. Модели звездчатых многогранников // Квант. – 1981. - № 2.
3. Савченко В. Полуправильные многогранники // Квант. – 1976. - № 1.
4. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
5. Энциклопедия элементарной математики. – Кн. V. Геометрия. – М.: Наука, 1966.