СЕЧЕНИЯ ЦИЛИНДРА И КОНУСА

СЕЧЕНИЯ ЦИЛИНДРА И КОНУСА     Рассмотрим цилиндрическую поверхность, образованную вращением вокруг оси прямой, параллельной этой оси.
    Теорема. Сечением цилиндрической поверхности плоскостью является эллипс.
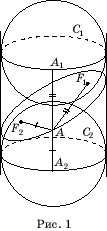
    Доказательство. Пусть плоскость a пересекает цилиндрическую поверхность. Впишем в эту поверхность две сферы, касающиеся плоскости a в некоторых точках F₁, F₂ и цилиндрической поверхности по окружностям C₁, С₂ (рис. 1). Пусть A – произвольная точка сечения. Проведем через нее образующую и обозначим через А_1,А₂ точки пересечения этой образующей с окружностями C₁, C₂соответственно. Заметим, что прямая A₁A₂является касательной к обеим сферам. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF₁= AA₁, AF₂ = AA₂. Поэтому AF₁ + AF₂ = AA₁ + AA₂ = A₁A₂. Но длина отрезка А₁А₂ есть расстояние между плоскостями окружностей C₁, C₂. Поэтому оно не зависит от выбора точки А сечения, и, следовательно, сечение является эллипсом с фокусами F₁ и F₂.

Рассмотрим еще одно свойство сечений цилиндра плоскостью, а именно, связь этих сечений с тригонометрическими функциями.
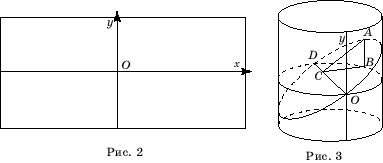
Возьмем прямоугольный лист бумаги и нарисуем на нем оси координат Ox и Oy параллельно соответствующим сторонам (рис. 2). Затем свернем этот лист в прямой круговой цилиндр, радиус основания которого примем за единицу. Ось Ox свернется в окружность радиуса 1, а ось Oy станет образующей цилиндра (рис. 3). Через диаметр OD полученной окружности проведем сечение, составляющее с плоскостью окружности угол в 45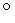

. В этом случае сечением будет эллипс.
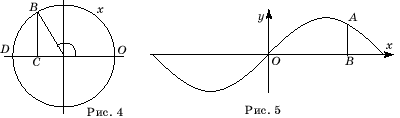
Развернем цилиндр обратно в прямоугольник. При этом эллипс развернется в кривую, являющуюся частью синусоиды. Для доказательства этого из произвольной точки A на эллипсе опустим перпендикуляры на плоскость окружности и диаметр окружности OD. Получим соответственно точки B и C. Треугольник ABC прямоугольный и равнобедренный. Следовательно, AB = BC.Заметим, что BC = sin x, где x - длина дуги OB. Для этого достаточно обратиться к рисунку 4 и вспомнить определение синуса. Таким образом, AB = sin x, где x = OB, т. е. эта кривая является частью синусоиды с уравнением y= sin x (рис. 5).

    Выясним теперь, что получается в сечениях конической поверхности плоскостью.
    Ясно, что если плоскость сечения параллельна плоскости основания конуса и не проходит через его вершину конуса, то в сечении получается окружность.
    Исследуем другие возможные случаи сечения конической поверхности плоскостью, не проходящей через вершину конуса.
    Теорема. Если плоскость образует с осью конуса угол, больший, чем угол между образующей и этой осью, то в сечении конической поверхности получается эллипс.
    Доказательство. Докажем, что сечение удовлетворяет фокальному свойству эллипса: сумма расстояний от произвольной точки сечения до двух данных точек есть величина постоянная.
    Впишем в коническую поверхность две сферы, касающиеся плоскости сечения в некоторых точках F₁, F₂ и конической поверхности по окружностям C₁ и C₂ соответственно (рис. 6).

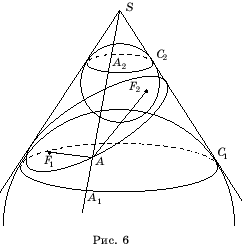     Пусть А – произвольная точка сечения. Проведем образующую AS и обозначим через А_1,А₂ точки ее пересечения с окружностями C₁, C₂ соответственно. Заметим, что прямая AS является касательной к обеим сферам. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF₁ = AA₁, AF₂ = AA₂. Поэтому AF₁ + AF₂ = AA₁ + AA₂ = A₁A₂. Но длина отрезка А₁А₂ не зависит от выбора точки А сечения. Она равна образующей соответствующего усеченного конуса. Поэтому сумма расстояний от точки А до точек F₁, F₂ будет постоянной.
    Теорема. Если плоскость образует с осью конуса угол, равный углу между образующей и этой осью, то в сечении конической поверхности получается парабола.
    Доказательство. Напомним, что параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой d, называемой директрисой, лежащих в этой плоскости. Впишем в коническую поверхность сферу, касающуюся плоскости a в некоторой точке F и конической поверхности по окружности C, лежащей в плоскости b, перпендикулярной оси. Плоскости a и b образуют между собой угол 90

-j и пересекаются по некоторой прямой d (рис. 7).

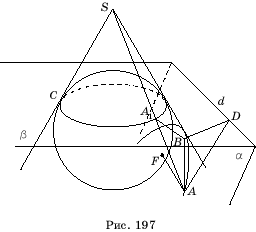Пусть А - произвольная точка сечения. Проведем образующую AS и обозначим через А₁ точку ее пересечения с окружностью C. Заметим, что прямая ASявляется касательной к сфере. Прямая AF также является касательной. Отрезки АF и АА₁равны как отрезки касательных, проведенных к сфере из одной точки.
Опустим из точки А перпендикуляр АВ на плоскость b и перпендикуляр АD на прямую d. Угол А₁АВ равен j. Угол АDВ является углом между плоскостями a и b и поэтому равен 90

-j. Следовательно, угол BAD равен j.
    Прямоугольные треугольники АВА₁ и АВD равны, так как имеют общий катет и соответственно равные углы. Поэтому АА₁ =АD. Окончательно получаем равенство AF = AD, которое означает, что расстояние от произвольной точки сечения до точки F равно расстоянию от этой точки до прямой d, т. е. сечением конической поверхности в этом случае является парабола.
    Теорема. Если плоскость образует с осью конуса угол, меньший угла между образующей и этой осью, то в сечении конической поверхности получается гипербола.
    Доказательство. Напомним, что гиперболой называется геометрическое место точек на плоскости, модуль разности расстояний от которых до двух заданных точек плоскости постоянен. Впишем в коническую поверхность сферы, касающиеся плоскости сечения в некоторых точках F₁ и F₂ и конической поверхности по окружностям C₁и C₂ соответственно.

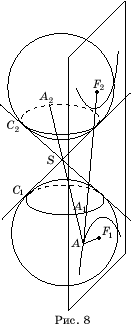Пусть А - точка сечения, расположенная в той же части конической поверхности, что и точка F₁ (рис. 8). Проведем образующую AS и обозначим через А₁,А₂ точки ее пересечения с окружностями C₁, C₂соответственно.Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF₁ = AA₁, AF₂ = AA₂. Поэтому AF₂ - AF₁ = AA₂ - AA₁ = A₁A₂. Но длина отрезка А₁А₂ не зависит от выбора точки А сечения. Она равна сумме образующих соответствующих конусов. Следовательно, разность AF₂ - AF₁ расстояний от точки А до точек F₁, F₂ будет постоянной. Аналогичным образом показывается, что если точка A расположена в той же части конической поверхности, что и точка F₂, то разностьAF₁ – AF₂ будет постоянной. Таким образом, сечением конической поверхности в этом случае является гипербола. Исторические сведения Конические сечения с древних времен привлекали к себе внимание ученых. Так древнегреческий ученый Менехм (IV в. до н. э.) пользовался параболой и гиперболой для решения знаменитой задачи удвоения куба. Исследовали свойства конических сечений Евклид (IV в. до н. э.) и Архимед (III в. до н. э.). Полное и систематическое учение об этих кривых было изложено Аполлонием Пергским (III - II вв. до н. э.) в восьмитомном труде "Конические сечения". Там он впервые показал, как можно получить эти кривые, рассекая один и тот же конус плоскостью под разными углами. Он же ввел термины "эллипс", "парабола" и "гипербола", означающие в переводе с греческого соответственно "недостаток", "приложение" и "избыток". Происхождение этих названий связано с задачей построения прямоугольника с заданным основанием, равновеликого данному квадрату. Переводя с геометрического языка, которым пользовался Аполлоний, на современный алгебраический язык, получаем уравнение y² = 2px + lx², где эллипсу соответствует отрицательное, гиперболе – положительное, а параболе – равное нулю значение второго члена в правой части. Таким образом, для параболы площадь квадрата, построенного на ординате y, равна площади прямоугольника со сторонами 2p и x. Для эллипса площадь прямоугольника меньше, а для гиперболы - больше площади соответствующего квадрата.
Интерес к коническим сечениям особенно возрос после того как Г. Галилей (1564-1642) установил, что тело, брошенное под углом к горизонту, двигается по параболе, а И. Кеплер сформулировал законы движения планет, согласно которым они описывают эллипсы. Позднее было установлено, что кометы и другие небесные тела движутся по эллипсам, параболам или гиперболам в зависимости от их начальной скорости.

Литература
1. Болтянский В.Г. Элементарная геометрия. – М.: Просвещение, 1985.
2. Виленкин Н.Я. Функции в природе и технике. – М.: Просвещение, 1985.
3. Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – М.: Наука, 1981.
4. Дорфман А.Г. Оптика конических сечений. – М.: Гос. изд. физ.-мат. лит-ры, 1959./Популярные лекции по математике. Выпуск 31.
5. Пидоу Д. Геометрия и искусство. – М.: Мир. 1979.
6. Факультативные курсы по математике для 10-11 классов / Атанасян Л.С. и др. М.: НИИ школ МНО РСФСР, 1989.
7. Школьная энциклопедия. Математика. – М.: Дрофа, 1997.
8. Энциклопедический словарь юного математика. – М.: Педагогика, 1997.
9. Энциклопедия элементарной математики, книги I-V. – М.: Физматгиз, Москва, 1961 - 1966.
10. Журнал Квант: 1975, № 1, № 3, № 4, № 5; 1987, № 6; 1990, № 9.