ФИГУРЫ ВРАЩЕНИЯ

ФИГУРЫ ВРАЩЕНИЯ     Важным классом фигур в пространстве, помимо многогранников, является класс фигур, называемых фигурами вращения.
    Прежде чем дать определение фигуры вращения, рассмотрим понятие поворота в пространстве вокруг прямой, которое является аналогом понятия поворота на плоскости вокруг точки.
    Пусть в пространстве задана прямая a и точка A, не принадлежащая этой прямой (рис. 1). Через точку A проведем плоскость a, перпендикулярную прямой a, и точку пересечения a и a обозначим O. Говорят, что точка A' пространства получается из точки A поворотом вокруг прямой a на угол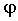

, если в плоскости a точка A' получается из точки A поворотом вокруг центра O на угол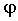

Определение. Преобразование пространства, при котором точки прямой a остаются на месте, а все остальные точки поворачиваются вокруг этой прямой (в одном и том же направлении) на угол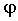

называется поворотом или вращением. Прямая a при этом называется осью вращения.
    Говорят,что фигура Ф в пространстве получена вращением фигуры F вокруг оси a, если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси a. Фигура Ф при этом называется фигурой вращения.
    Например, при вращении точки A вокруг прямой a (рис. 2) получается окружность с центром в точке O, являющейся пересечением прямой а с плоскостью, проходящей через точку А и перпендикулярной прямой а.
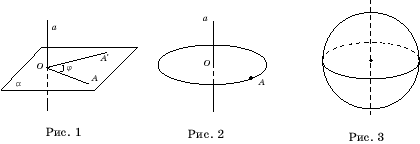
    Сфера получается вращением окружности вокруг ее диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра (рис. 3).
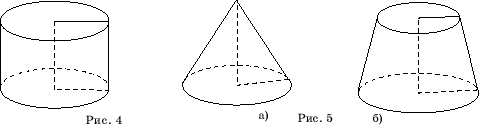
    Цилиндр получается вращением прямоугольника вокруг одной из его сторон (рис. 4).
    Конус получается вращением прямоугольного треугольника вокруг одного из его катетов (рис. 5, а).
    Усеченный конус получается вращением трапеции, один из углов которой является прямым, вокруг боковой стороны, прилегающей к этому углу (рис. 5, б).

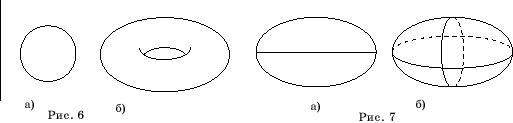
Если окружность вращать вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек (рис. 6, а), то полученная поверхность вращения называется тором и по форме напоминает баранку или бублик (рис. 6, б).
При вращении эллипса вокруг его оси (рис. 7, а) получается поверхность, называемая эллипсоидом вращения (рис. 7, б).

При вращении параболы вокруг ее оси (рис. 8, а) получается поверхность, называемая параболоидом вращения (рис. 8, б).
При вращении гиперболы вокруг ее оси (рис. 9, а) получается поверхность, называемая гиперболоидом вращения (рис. 9, б).

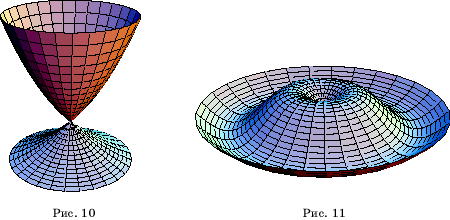
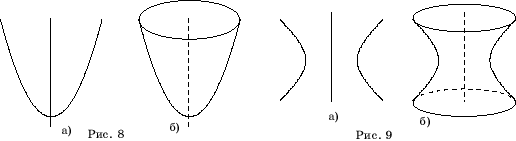При вращении графика показательной функции вокруг оси Oy получается поверхность, изображенная на рисунке 10.
При вращении синусоиды вокруг оси Oy получается поверхность, изображенная на рисунке 11.

Выясним, какие фигуры могут получаться при вращении прямой.
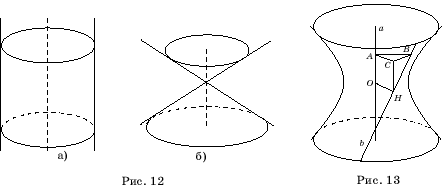
Если прямая параллельна оси, то при вращении получается фигура, называемая цилиндрической поверхностью (рис. 12, а). Если прямая пересекает ось и не перпендикулярна ей, то при вращении получается фигура, называемая конической поверхностью (рис. 12, б).

    Если прямая пересекает ось и перпендикулярна ей, то при вращении получается плоскость. Если же прямая перпендикулярна оси и не пересекается с ней, то при вращении получается плоскость без внутренности круга, радиус которого равен расстоянию от прямой до оси.
    Рассмотрим оставшийся случай взаимного расположения прямой и оси вращения.
    Теорема. При вращении прямой, скрещивающейся с осью вращения и не перпендикулярной ей, получается гиперболоид вращения.
    Доказательство. Пусть a и b - скрещивающиеся прямые, OH - их общий перпендикуляр (рис. 13). Напомним, что длина d отрезка OH называется расстоянием между прямыми a и b. Она является наименьшей из длин отрезков, соединяющих точки прямых a и b. Поэтому при вращении точек прямой b вокруг оси a окружность наименьшего радиуса будет получаться при вращении точки H. Рассмотрим произвольную точку B на прямой b, отличную от H, и опустим из нее перпендикуляр BA на прямую a. При вращении точка B описывает окружность, радиус которой равен AB. Выразим этот радиус через d. Для этого через точку H проведем прямую, параллельную a, и через точку A - прямую, параллельную OH. Точку пересечения этих прямых обозначим C. Пусть расстояние AB равно x, расстояние OA равно y и угол BHC равен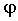

. Треугольник ABC - прямоугольный, катет AC равен d, катет BC равен y·tga. Поэтому выполняется равенство x² = d² + y²tg²a. Перенеся слагаемое, содержащее y, в левую часть равенства и разделив обе части полученного равенства на d², получим уравнение

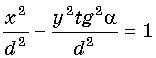, которое представляет собой уравнение гиперболы. При вращении этой гиперболы получается та же самая фигура, что и при вращении прямой, скрещивающейся с осью вращения. Следовательно, искомой фигурой вращения является гиперболоид вращения.
    Из доказанной теоремы, в частности, следует интересная особенность гиперболоидов вращения. Несмотря на искривленность их поверхностей, все они состоят из прямолинейных отрезков. Поэтому форма гиперболоида вращения часто используется в архитектурных сооружениях. Так, Шаболовская радиобашня в Москве, построенная по проекту замечательного русского инженера, почетного академика В.Г. Шухова (1853-1939), составлена из частей гиперболоидов вращения. Ее особенностью является то, что она, в действительности, состоит из прямолинейных конструкций - металлических стержней.
    Заметим, что поверхность фигуры, получающейся при вращении многогранника, определяется вращением некоторых его ребер. При этом, если ребро параллельно оси, то при вращении оно дает боковую поверхность цилиндра. Если ребро не параллельно оси, но лежит с ней в одной плоскости, то при вращении оно дает часть конической поверхности. А именно: а) если ребро не пересекает ось, то получается боковая поверхность усеченного конуса; б) если одна вершина ребра принадлежит оси, то получается боковая поверхность конуса; в) если ребро пересекает ось, то получается поверхность, состоящая из двух боковых поверхностей конусов с общей вершиной. Если же ребро многогранника скрещивается с осью вращения, то получается поверхность, являющаяся частью гиперболоида вращения.
    Таким образом, поверхность вращения многогранника может состоять из боковых поверхностей цилиндра, конуса, усеченного конуса и частей поверхностей гиперболоидов вращения. Никаких других поверхностей при вращении многогранника получиться не может.
    Выясним, например, какая фигура получается при вращении куба A...D₁ вокруг диагонали AC₁.
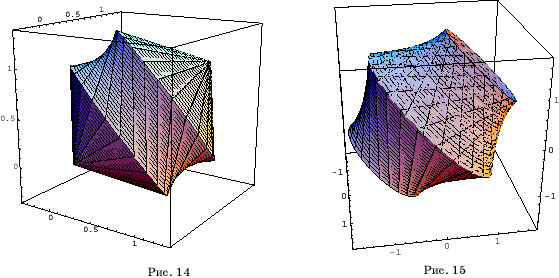
    Ребра этого куба, выходящие из вершины A и вершины C₁, при вращении дадут два конуса с этими вершинами. Поверхность вращения, заключенная между этими конусами получается при вращении ребер куба, скрещивающихся с диагональю AC₁. Следовательно, она является частью гиперболоида вращения, и вся поверхность вращения выглядит так, как показано на рисунке 14.
    При вращении куба вокруг прямой, проходящей через середины противоположных ребер получается поверхность, состоящая из двух кругов и двух частей гиперболоидов вращения (рис. 15).

Литература
1. Баврин И.И., Садчиков В.А. Новые задачи по стереометрии: Фигуры вращения правильных многогранников. – М.: ВЛАДОС, 2000. – 208 с.
2. Энциклопедия элементарной математики. Книга V. Геометрия. - М.: Наука, 1966, с.7, с.130.
4. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
5. Глейзер Г.И. История математики в школе. IX-X классы. – М.: Просвещение, 1983.
6. Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1966.
7. Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – 3-е изд. – М.: Наука, 1981.
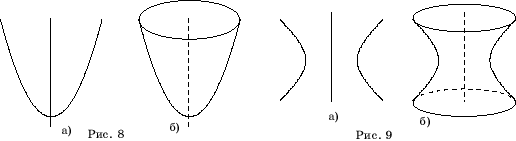
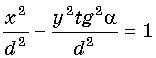