ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ И ЛИНИИ В ТРЕУГОЛЬНИКЕ
К
числу замечательных линий и точек в треугольнике, изучаемых в основном курсе
геометрии, относятся:
а) медианы и точка
пересечения медиан (центроид).
б) биссектрисы
и точка пересечения биссектрис (центр вписанной окружности);
в) точка пересечения
серединных перпендикуляров (центр описанной окружности);
г) высоты и точка пересечения
высот (ортоцентр);
Начнем с медиан треугольника.
Теорема. Медианы треугольника
пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
Доказательство. В треугольнике A BC проведем медианы AA1 и CC1 и их точку пересечения
обозначим M.
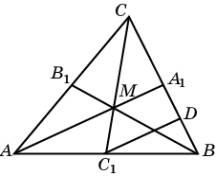
Через
точку C1 проведем прямую, параллельную AA1 и ее точку пересечения с BC обозначим
D. Тогда D – середина BA1, следовательно, CA1:A1D
= 2:1. По
теореме Фалеса, CM :MC1 = 2:1. Таким образом,
медиана AA1 пересекает медиану CC1 в точке M,
делящей медиану CC1 в отношении 2:1. Аналогично, медиана BB1 пересекает медиану CC1 в точке, делящей медиану CC1 в отношении 2:1, т.е. точке
M.
Одним из основных методов решения задач, в которых
участвуют медианы треугольника, является метод «удвоения медианы». Рассмотрим
его на примере решения следующих задач.
Задача 1. Докажите, что медиана треугольника лежит ближе к
большей стороне, т.е. если в треугольнике ABC AC
> BC, то для медианы CC1 выполняется неравенство ÐACC1 < ÐBCC1.
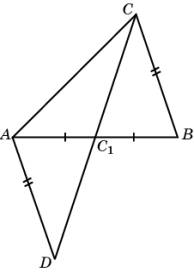
Решение. Продолжим медиану CC1 и отложим отрезок C1D,
равный CC1. Треугольник AC1D равен
треугольнику BC1C по двум сторонам и углу
между ними. Следовательно, AD = BC, ÐADC1 = ÐBCC1. В треугольнике ACD AC > AD. Так как против большей
стороны треугольника лежит больший угол, то ÐADC > ÐACD. Следовательно, выполняется
неравенство ÐACC1
< ÐBCC1.
Задача 2. Докажите, что медиана треугольника меньше полусуммы
сторон, выходящих из той же вершины, т.е. для медианы CC1 треугольника ABC выполняется
неравенство CC1 < (AC + BC)/2.
Решение. Продолжим медиану CC1 и отложим отрезок C1D,
равный CC1. Треугольник AC1D равен
треугольнику BC1C по двум сторонам и углу
между ними. Следовательно, AD = BC.
В силу неравенства треугольника имеем неравенство CD < AC
+ AD. Следовательно, выполняется неравенство CC1 < (AC
+ BC)/2.
Задача 3. Площадь треугольника ABC равна 1. Найдите площадь
треугольника, стороны которого равны медианам данного треугольника.
Решение. Пусть AA1, BB1, CC1 – медианы треугольника ABC,
пересекающиеся в точке M. Продолжим медиану CC1 и отложим отрезок C1D,
равный MC1.
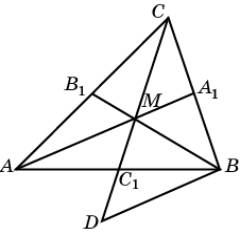
Площадь треугольника BMC равна
1/3, и его стороны равны 2/3 медиан исходного треугольника. Следовательно,
площадь треугольника, стороны которого равны медианам данного треугольника,
равна 3/4.
Выведем формулу, выражающую медианы треугольника через его стороны. Пусть стороны треугольника ABC равны a, b, c. Искомую длину медианы CD обозначим mc. По теореме косинусов имеем:
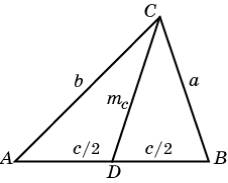
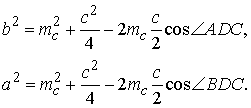
Складывая эти два равенства
и учитывая, что cosÐADC
= –cosÐBDC,
получаем равенство 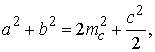 из которого находим
из которого находим
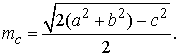
Перейдем к биссектрисам треугольника.
В школьном курсе геометрии доказывается, что
биссектрисы треугольника пересекаются в одной точке – центре вписанной
окружности.
Рассмотрим одну из наиболее важных теорем,
относящихся к биссектрисам треугольника.
Теорема. Биссектриса треугольника делит его сторону на
части, пропорциональные прилежащим к ней сторонам, т.е. если CD –
биссектриса треугольника ABC, то AD : DB
= AC : BC.
Доказательство. Через точку B проведем прямую,
параллельную биссектрисе CD и ее точку пересечения с
прямой AC обозначим E.
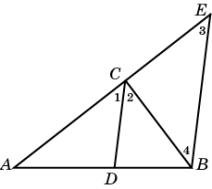
Углы 1 и 3 равны, как
соответственные, углы 2 и 4 равны, как внутренние накрест лежащие.
Следовательно, треугольник BCE равнобедренный, BC
= CE. По теореме о пропорциональных отрезках AD :
DB = AC : CE, следовательно,
AD : DB = AC : BC.
Задача 1. В треугольнике ABC AC
= 4, BC
= 3, AB
= 5, CD –
биссектриса. Найдите площадь треугольника ACD.
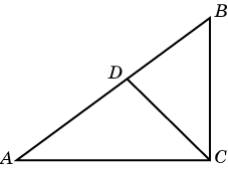
Решение. Площадь треугольника ABC равна
6. Сторона AD составляет 4/7 стороны AB.
Следовательно, площадь треугольника ACD равна ![]()
Задача 2. В треугольнике ABC AC
= 4, BC
= 3, AB
= 5. CD –
биссектриса, BE – медиана, F –
их точка пересечения. Найдите площадь четырехугольника ADFE.
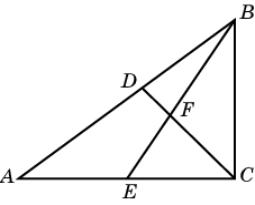
Решение. Площадь треугольника ABE равна 3. Проведем среднюю
линию EG треугольника ACD.
BD : DA = 3:4, BD :
DG = 3:2. Следовательно,
BD : AB = 3:7, BF : BE
= 3:5.
Следовательно, площадь треугольника BDF равна 27/35. Площадь
четырехугольника ADFE равна ![]()
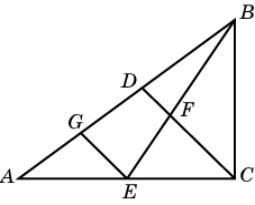
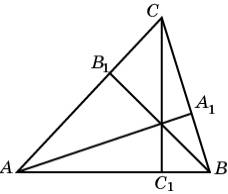
Выведем формулу, выражающую биссектрисы треугольника
через его стороны. Пусть стороны треугольника ABC равны a, b, c. Искомую длину биссектрисы CD обозначим
lc.
Отрезки AD и BD обозначим c’ и c”
соответственно. Заметим, что ![]()
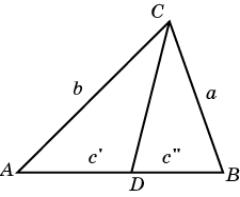
По теореме косинусов имеем:
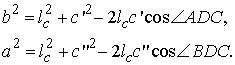
Умножим первое равенство на c”, второе на c’
и сложим.
Получим ![]() Откуда
Откуда 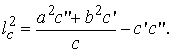 Непосредственная
проверка показывает, что
Непосредственная
проверка показывает, что 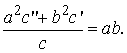 Окончательно получаем
следующую формулу
Окончательно получаем
следующую формулу
![]()
Задача. Докажите, что биссектриса CC1 треугольника ABC делится
точкой O пересечения биссектрис в
отношении (a+b) : c,
считая от вершины, где a, b, c –
стороны треугольника, лежащие против соответствующих вершин A, B, C.
Рассмотрим высоты
треугольника.
В школьном курсе геометрии доказывается, что высоты треугольника или их продолжения пересекаются в одной точке – ортоцентре.
Рассмотрим некоторые
свойства, связанные с высотами треугольника.
Свойство 1. Если AA1, BB1, CC1 – высоты треугольника ABC,
то угол A1AC равен углу B1BC.
Доказательство. Прямоугольные треугольники A1AC и B1BC
имеют общий острый угол. Следовательно, равны и два других их острых угла A1AC и B1BC.
Свойство 2. Если AA1, BB1, CC1 – высоты треугольника ABC,
то треугольник ABC подобен треугольнику A1B1C.
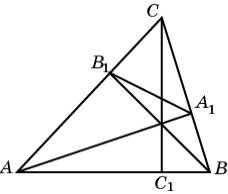
Доказательство. Из подобия треугольников A1AC и B1BC
(предыдущее свойство) следует, что AC : A1C
= BC : B1C. Следовательно,
треугольники ABC и A1B1C подобны,
как треугольники имеющие общий угол и соответственно пропорциональные стороны,
прилежащие к этому углу.
Свойство 3. Если AA1, BB1, CC1 – высоты треугольника ABC,
то угол A1C1C равен
углу B1C1C.
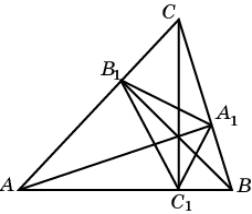
Доказательство. На
сторонах треугольника ABC, как на диаметрах, опишем
окружности.
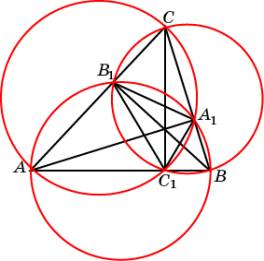
Они пройдут через
точки A1, B1, C1. Угол A1C1C равен
углу A1AC как углы, опирающиеся на
одну дугу A1C. Угол A1AC равен
углу B1BC по свойству 1. Угол B1BC равен
углу B1C1C, как
углы, опирающиеся на одну дугу B1C. Следовательно,
угол A1C1C равен
углу B1C1C.
Свойство 4. Точки A’, B’, C’, симметричные точке H пересечения
высот AA1, BB1, CC1 треугольника ABC относительно
его сторон, принадлежат окружности, описанной около этого треугольника.
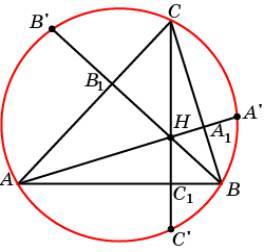
Доказательство.
Покажем, что точка C’ принадлежит описанной
окружности. Для этого достаточно показать, что сумма углов AC’B и ACB равна
180о. Действительно, углы AC’B и AHB равны,
как симметричные. Углы AHB и A1HB1 равны, как вертикальные.
Углы A1HB1 и A1CB1 в сумме составляют 180о.
Следовательно, сумма углов AC’B и ACB равна
180о.
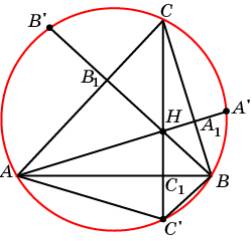
Задача.
Докажите, что для высот ha, hb, hc треугольника и радиуса r окружности,
вписанной в этот треугольник, имеет место равенство
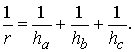
Рассмотрим некоторые другие замечательные точки и линии в треугольнике.
Точка Торричелли
Путь дан
треугольник ABC. Точкой Торричелли этого треугольника называется такая
точка O, из которой стороны данного треугольника видны под углом 120° (рис. 1, а), т.е. углы AOB, AOC и BOC равны 120о.
Докажем, что в случае, если
все углы треугольника меньше 120° , то точка
Торричелли существует.
На стороне AB
треугольника ABC построим равносторонний треугольник ABC' (рис.
1, а), и опишем около него окружность. Отрезок AB стягивает дугу этой
окружности величиной 120° . Следовательно, точки этой дуги, отличные от A
и B, обладают тем свойством, что отрезок AB виден из них под
углом 120° . Аналогичным образом, на стороне AC
треугольника ABC построим равносторонний треугольник ACB' (рис.
1, а), и опишем около него окружность. Точки соответствующей дуги, отличные A
и C, обладают тем свойством, что отрезок AC виден из них под
углом 120° . В случае, когда углы треугольника меньше 120° , эти дуги пересекаются в некоторой внутренней точке O. В этом
случае ÐAOB = 120°, ÐAOC = 120°. Следовательно, и ÐBOC = 120°. Поэтому точка O является
искомой.
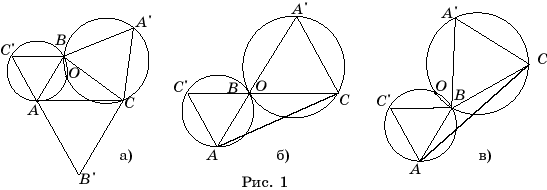
В случае,
когда один из углов треугольника, например ABC, равен 120° , точкой пересечения дуг окружностей будет точка B (рис. 1, б).
В этом случае точки Торричелли не существует, так как нельзя говорить об углах,
под которыми видны из этой точки стороны AB и BC.
В случае, когда один из углов
треугольника, например ABC, больше 120° (рис. 1, в),
соответствующие дуги окружностей не пересекаются. Сами окружности пересекаются
в некоторой точке O, из которой стороны AB и BC видны под
углом 60°. В этом случае точки Торричелли также не существует.
Таким образом, во всех трех
случаях окружности, описанные около равносторонних треугольников, построенных
на сторонах данного треугольника, пересекаются в одной точке. Если углы
треугольника меньше 120° , то эта точка лежит внутри треугольника и является
точкой Торричелли.
Задача. Докажите, что отрезки, соединяющие вершины
треугольника с соответствующими вершинами правильных треугольников, построенных
на сторонах данного треугольника в его внешней области, пересекаются в одной
точке.
Окружность девяти точек
Теорема.Пусть в треугольнике ABC (рис. 2), H – точка пересечения высот треугольника; точки A1, B1, C1обозначают основания высот; A2, B2, C2 – середины соответствующих сторон; A3, B3, C3– середины отрезков AH, BH и CH. Тогда точки A1, B1, C1, A2, B2, C2, A3, B3,C3 лежат на одной окружности, называемой окружностью девяти точек.
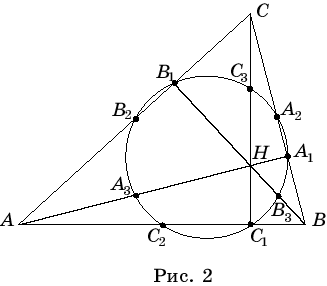
Действительно, A3B2 – средняя линия треугольника AHC и, следовательно, A3B2|| CC1. B2A2 – средняя линия треугольника ABC и, следовательно, B2A2 || AB. Так как CC1 ^ AB, то ÐA3B2A2 = 90° . Аналогично, ÐA3C2A2= 90°. Поэтому точки A2, B2, C2, A3лежат на одной окружности с диаметром A2A3. Так как AA1 ^BC, то точка A1 также принадлежит этой окружности. Таким образом, точки A1и A3лежат на окружности, описанной около треугольника A2B2C2. Аналогичным образом показывается, что точки B1 и B3, C1 и C3 лежат на этой окружности. Значит, все девять точек лежат на одной окружности. Что и требовалось доказать.
Прямая Эйлера
Теорема. В треугольнике центр
описанной окружности, точка пересечения медиан, точка пересечения высот и центр
окружности девяти точек лежат на одной прямой, называемой прямой Эйлера. При
этом центр окружности девяти точек лежит посередине между центром пересечения высот
и центром описанной окружности.
Действительно, пусть в
треугольнике ABC (рис. 3), точка O – центр описанной окружности; G
– точка пересечения медиан, H –
точка пересечения высот. Рассмотрим гомотетию с центром в точке G и
коэффициентом -0,5. Она переводит вершины A, B, C треугольника
ABC соответственно
в точки A2, B2, C2. Высоты
треугольника ABC перейдут в серединные перпендикуляры к сторонам этого
треугольника и, следовательно, точка пересечения высот H перейдет в
точку пересечения серединных перпендикуляров O. Значит, точки O, G, H лежат
на одной прямой.
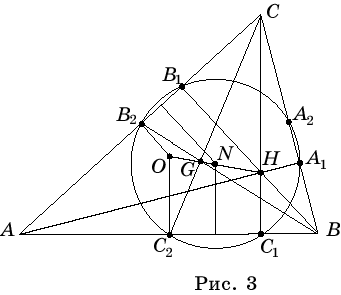
Покажем, что середина N отрезка OH является центром окружности девяти точек. Действительно, C1C2– хорда окружности девяти точек. Поэтому серединный перпендикуляр к этой хорде является диаметром и пересекает OH в середине N. Аналогично, серединный перпендикуляр к хорде B1B2 является диаметром и пересекает OH в той же точке N. Значит N– центр окружности девяти точек. Что и требовалось доказать.
Задача. Докажите, что радиус
окружности Эйлера в два раза меньше радиуса окружности, описанной около
исходного треугольника.
Прямая Симсона
Теорема. Для произвольного
треугольника основания перпендикуляров, опущенных из любой точки описанной
окружности на стороны треугольника или их продолжения, лежат на одной прямой,
называемой прямой Симсона.
Действительно, пусть P
– произвольная точка, лежащая на окружности, описанной около треугольника ABC;
D, E, F – основания перпендикуляров, опущенных из точки P на стороны
треугольника (рис. 4). Требуется доказать, что точки D, E, F лежат на
одной прямой.
Заметим, что в случае, если AP
проходит через центр окружности, то точки D и E совпадают с
вершинами B и C. В противном случае, один из углов ABP или
ACP острый, а другой – тупой. Из этого следует, что точки D и F
будут расположены по разные стороны от прямой BC и для того, чтобы
доказать, что точки D, E и F
лежат на одной прямой, достаточно проверить, что ÐCEF=ÐBED.
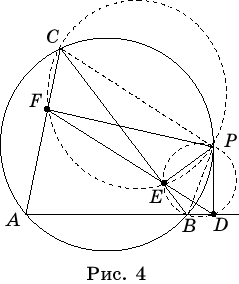
Опишем окружность с диаметром CP. Так как ÐCFP = ÐCEP = 90о, то точки E и F лежат на этой окружности. Поэтому ÐCEF =ÐCPF как вписанные углы, опирающиеся на одну дугу окружности. Далее, ÐCPF = 90о- ÐPCF = 90о- ÐDBP = ÐBPD. Опишем окружность с диаметром BP. Так как ÐBEP = ÐBDP = 90о, то точки F и D лежат на этой окружности. Поэтому ÐBPD =ÐBED. Следовательно, окончательно получаем, что ÐCEF =ÐBED. Значит точки D, E, F лежат на одной прямой.
Литература
1. Адамар Ж. Элементарная
геометрия. Часть I. Учпедгиз, Москва, 1948.
2. Перепелкин Д.И. Курс
элементарной геометрии. Часть I. ОГИЗ, Гостехиздат. Москва, Ленинград, 1948
3. Зетель С.И. Новая
геометрия треугольника. – М.: Учпедгиз, 1962.
4. Кокстер Г.С.М. Введение в
геометрию. – М.: Наука, 1966.
5. Коксетер Г.С.М., Грейтцер
С.Л. Новые встречи с геометрией. – М.: Наука, 1978.
6. Прасолов В.В. Задачи по
планиметрии. – Части I, II. – М.: Наука, 1986.
7. Шклярский Д.О., Ченцов
Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Часть 2.
Геометрия (Планиметрия). – М.: Государственное издательство
технико-теоретической литературы, 1952.