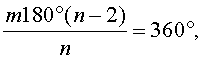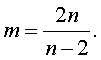ПАРКЕТЫ

ПАРКЕТЫ     Паркетом называется такое заполнение плоскости многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.
    Паркет называется правильным, если он состоит из правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом.
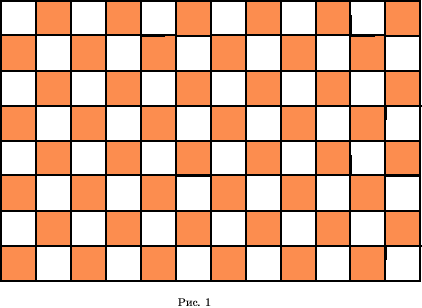
    Примеры правильных паркетов дают заполнения плоскости: а) квадратами (рис. 1);

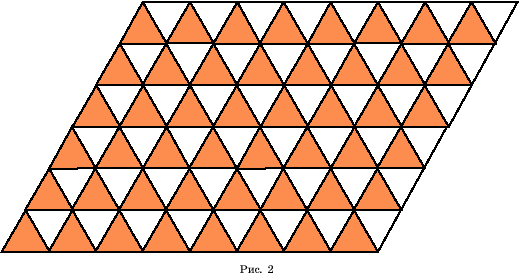
б) равносторонними треугольниками (рис. 2);

в) правильными шестиугольниками (рис. 3).

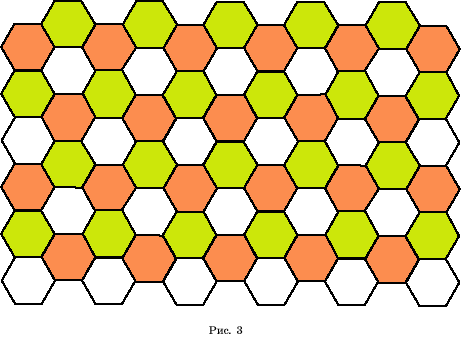Докажем, что другими равными правильными многоугольниками заполнить плоскость нельзя. Действительно, углы правильного n - угольника равны 180°(n - 2)/n. Заполним таблицу, состоящую из углов a правильных n-угольников.

N	3	4	5	6	7	8	9	10	11	12
a	60°	90°	108°	120°	128⁴/_7°	135°	140°	144°	147³/_11°	150°

Если в одной вершине паркета сходится m правильных n - угольников, то должно выполняться равенство

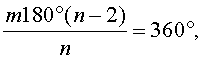откуда

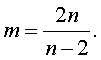
    Возможными допустимыми значениями n являются 3, 4 и 6. При остальных значениях n число m оказывается дробным. В частности, нельзя заполнить плоскость правильными пятиугольниками.
    Расширим способы составления паркетов из правильных многоугольников, разрешив использовать в них правильные многоугольники с различным числом сторон.
    Обозначим через a₁, a₂, … углы правильных многоугольников, имеющих общую вершину. Расположим их в порядке возрастания. Учитывая, что сумма всех таких углов должна быть равна 360° , составим таблицу, содержащую возможные наборы углов и укажем соответствующие паркеты.

a₁ a₂ a₃ a₄ a₅ a₆ a₁+a₂+…=360°

60° 60° 60° 60° 60° 60° Паркет из 3-ов (рис. 2)

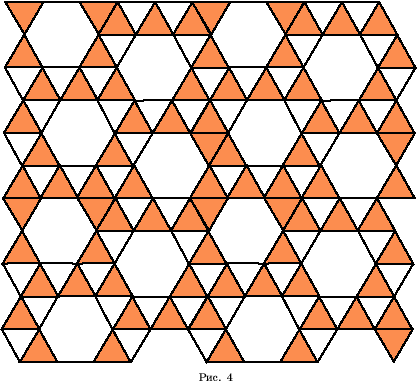
60° 60° 60° 60° 120° Паркет из 3-ов и 6-ов (рис. 4)

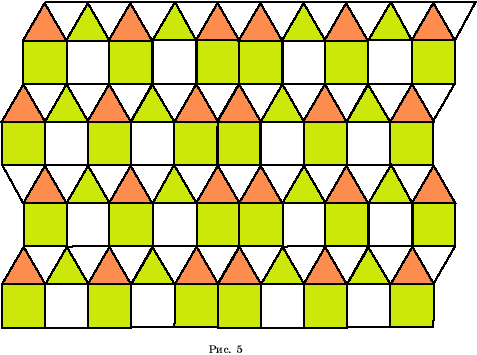
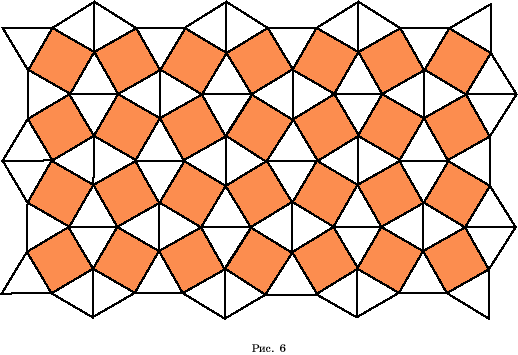
60° 60° 60° 90° 90° Два паркета из 3-в и 4-в
(рис. 5, 6)

60° 60° 90° 150° Нет паркета

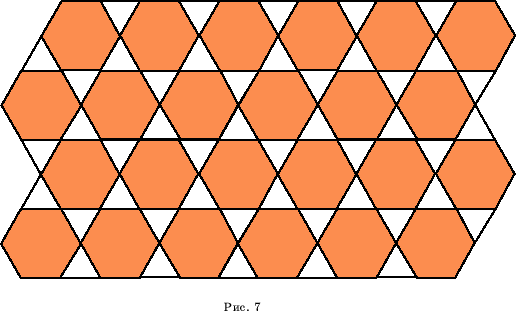
60° 60° 120° 120° Паркет из 3-в и 6-в (рис. 7)

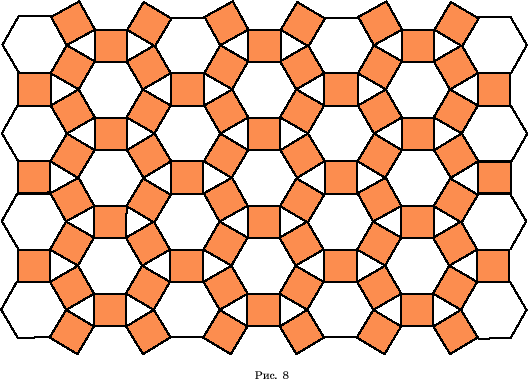
60° 90° 90° 120° Паркет из 3-в, 4-в и 6-в (рис. 8)

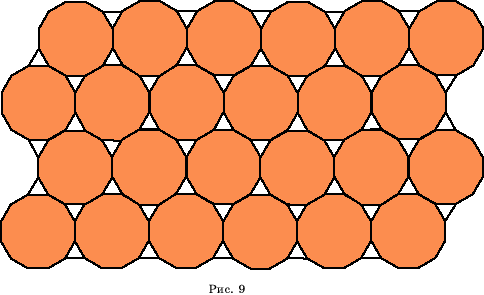
60° 150° 150° Паркет из 3-в и 12-в (рис. 9)

90° 90° 90° 90° Паркет из квадратов (рис. 1)

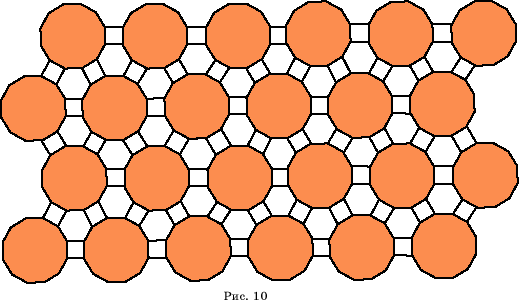
90° 120° 150° Паркет из 4-в, 6-в и 12-в (рис. 10)

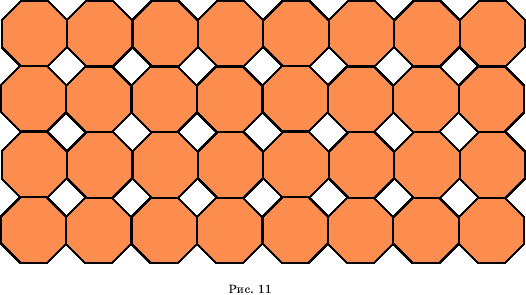
90° 135° 135° Паркет из 4-в и 8-в (рис. 11)

120° 120° 120° Паркет из 6-ов (рис. 3)

    Таким образом, всего имеется 11 типов правильных паркетов.
    Рассмотрим теперь вопрос о заполнении плоскости неправильными равными многоугольниками.
    Теорема. Для любого четырехугольника существует паркет, состоящий из четырехугольников равных исходному. Иначе говоря, четырехугольником произвольной формы можно заполнить всю плоскость.
    Доказательство. Пусть дан четырехугольник АВСD (рис. 12). Рассмотрим центрально симметричный ему четырехугольник относительно середины стороны АВ. Исходный четырехугольник АВСD обозначим цифрой 1, а симметричный - цифрой 2. Теперь четырехугольник 2 отразим симметрично относительно середины его стороны ВС. Полученный четырехугольник обозначим цифрой 3 и отразим его симметрично относительно середины его стороны CD. Полученный четырехугольник обозначим цифрой 4. Четырехугольники 1, 2, 3 и 4 примыкают к общей вершине углами А, В, С и D. А так как сумма углов четырехугольника равна 360° , то эти четырехугольники заполнят часть плоскости вокруг общей вершины. Такое же построение можно провести вокруг каждой новой вершины, что и даст искомое заполнение плоскости.

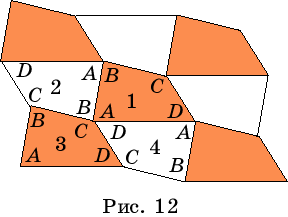Заметим, что четырехугольники, закрашенные одним цветом (рис. 12), получаются друг из друга параллельным переносом.
Заполнение плоскости может быть произведено не только многоугольниками, но и фигурами более сложного вида. Повторяющиеся равные фигуры являются основой составления орнаментов, с давних времен привлекавших к себе внимание людей. Знаменитый голландский художник Мариус Эшер (1898-1972) посвятил орнаментам несколько своих картин. Среди них: "Всадники" (рис. 13), "Летящие птицы" (рис. 14); "Ящерицы" (рис. 15).

Рис. 13

    Литература
    1. Кокстер Г.С.М. Введение в геометрию. – М.- Наука, 1966, с. 100.
    2. Васильев Н.Б. и др. Математические соревнования. Геометрия. – М.: Наука, 1974, с.15 /Библиотечка физико-математической школы, выпуск 4.
    3. Доморяд А.П. Математические игры и развлечения. – М.; 1961.
    5. Заславский А. Паркеты и разрезания //Квант. – 1999. - № 2. – С.32.
    6. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
    7. Смирнова И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе “Paint” //Математика в школе. – 2000. - № 8. – С.54.
    8. Журнал //Квант. 1979. - № 2. – С.9; 1980. - № 2. – С.25; 1986. - № 8. – С.3; 1987. - № 6. – С.27; 1987. - № 11. – С.21; 1989. - № 11. – С.57.
    9. Журнал //Математика в школе. 1967. - № 3. – С.75; 1986. № 1. – С.59;

a₁	a₂	a₃	a₄	a₅	a₆	a₁+a₂+…=360°
60°	60°	60°	60°	60°	60°	Паркет из 3-ов (рис. 2)
60°	60°	60°	60°	120°		Паркет из 3-ов и 6-ов (рис. 4)
60°	60°	60°	90°	90°		Два паркета из 3-в и 4-в (рис. 5, 6)
60°	60°	90°	150°			Нет паркета
60°	60°	120°	120°			Паркет из 3-в и 6-в (рис. 7)
60°	90°	90°	120°			Паркет из 3-в, 4-в и 6-в (рис. 8)
60°	150°	150°				Паркет из 3-в и 12-в (рис. 9)
90°	90°	90°	90°			Паркет из квадратов (рис. 1)
90°	120°	150°				Паркет из 4-в, 6-в и 12-в (рис. 10)
90°	135°	135°				Паркет из 4-в и 8-в (рис. 11)
120°	120°	120°				Паркет из 6-ов (рис. 3)