МНОГОГРАННЫЕ УГЛЫ
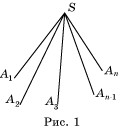
Многогранный угол является пространственным аналогом многоугольника. Напомним, что многоугольником на плоскости называется фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью. Будем считать аналогом точки на плоскости луч в пространстве и аналогом отрезка на плоскости плоский угол в пространстве. Тогда аналогом простой замкнутой ломаной на плоскости является поверхность, образованная конечным набором плоских углов A1SA2, A2SA3, …, An-1SAn, AnSA1 с общей вершиной S (рис. 1), в которых соседние углы не имеют общий точек, кроме точек общего луча, а несоседние углы не имеют общих точек, кроме общей вершины. Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется вершиной многогранного угла. Лучи SA1, …, SAn называются ребрами многогранного угла, а сами плоские углы A1SA2, A2SA3, …, An-1SAn, AnSA1 – гранями многогранного угла. Многогранный угол обозначается буквами SA1…An, указывающими вершину и точки на его ребрах. В зависимости от числа граней многогранные углы называются трехгранными, четырехгранными, пятигранными (рис. 2) и т. д.
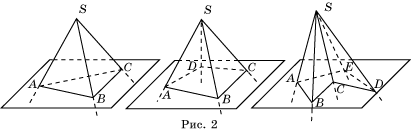
Многогранный угол называется выпуклым, если он является выпуклой
фигурой, т.е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок. На рисунке 2 трехгранный и
четырехгранный углы выпуклые, а пятигранный угол – нет.
Рассмотрим некоторые
свойства треугольников и аналогичные им свойства трехгранных углов.
Свойство 1 (Неравенство треугольника). Каждая сторона
треугольника меньше суммы двух других его сторон.
Аналогичным свойством для
трехгранных углов является следующее свойство.
Свойство 1'. Каждый плоский угол трехгранного угла меньше суммы
двух других его плоских углов.
Доказательство. Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC.
Тогда выполняются неравенства
ASB 
ASC < ASC + BSC;BSC ASC < ASC + ASB.
Таким образом, остается
доказать неравенство ASС < ASB + BSC.
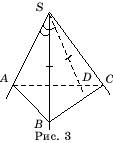
Отложим на грани ASC угол
ASD, равный ASB, и
точку B выберем так, чтобы SB = SD (рис. 3). Тогда треугольники ASB
и ASD равны (по двум сторонам и углу между ними) и, следовательно, AB
= AD. Воспользуемся неравенством треугольника AC < AB + BC.
Вычитая из обеих его частей AD = AB, получим неравенство DC < BC.
В треугольниках DSC и BSC одна
сторона общая (SC), SD = SB и DC < BC. В этом случае
против большей стороны лежит больший угол и, следовательно, DSC < BSC. Прибавляя к обеим частям
этого неравенства угол ASD, равный
ASB, получим требуемое неравенство ASС < ASB + BSC.
Следствие 1. Сумма плоских углов
трехгранного угла меньше 360°.
Доказательство. Пусть SABC – данный трехгранный угол.
Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS,
ACS и углом BAC. В силу доказанного свойства, имеет место
неравенство BAС < BAS + CAS. Аналогично, для
трехгранных углов с вершинами B и С имеют место
неравенства: ABС
< ABS + CBS, ACB < ACS + BCS. Складывая эти
неравенства и учитывая, что сумма углов треугольника ABC равна 180°, получаем 180°< BAS +CAS
+ ABS
+ CBS +BCS + ACS = 180° - ASB +
180° - BSC + 180° - ASC. Следовательно, ASB + BSC + ASC < 360° .
Следствие 2. Сумма плоских углов выпуклого многогранного угла
меньше 360
.
Доказательство аналогично
предыдущему.
Следствие 3. Сумма двугранных углов трехгранного угла больше 180°.
Доказательство. Пусть SABC – трехгранный угол. Выберем
какую-нибудь точку P внутри него и опустим из нее перпендикуляры PA1, PB1, PC1 на
грани (рис. 4).
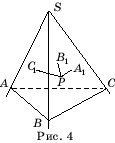
Плоские углы B1PC1, A1PC1, A1PB1 дополняют
соответствующие двугранные углы с ребрами SA, SB, SC до 180° . Следовательно, сумма этих двугранных углов равна 540°- (B1PC1 +A1PC1+ A1PB1).
Учитывая, что сумма плоских углов трехгранного с вершиной P угла меньше
360° , получаем, что сумма двугранных углов исходного
трехгранного угла больше 180°.
Свойство 2. Биссектрисы треугольника пересекаются в одной точке.
Свойство 2'.
Биссектральные плоскости двугранных углов трехгранного угла пересекаются по
одной прямой.
Доказательство аналогично
плоскому случаю. А именно, пусть SABC – трехгранный угол. Биссектральная
плоскость двугранного угла SA является ГМТ угла, равноудаленных от его
граней ASC и ASB. Аналогично, биссектральная плоскость
двугранного угла SB является ГМТ угла, равноудаленных от его граней
BSA и BSC. Линия их
пересечения SO будет равноудалена от всех граней трехгранного угла и, следовательно,
через нее будет проходить биссектральная плоскость двугранного угла SC.
Свойство 3. Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
Свойство 3'. Плоскости, проходящие через биссектрисы граней
трехгранного угла и перпендикулярные этим граням, пересекаются по одной прямой.
Доказательство аналогично
доказательству предыдущего свойства.
Свойство 4. Медианы треугольника пересекаются в одной точке.
Свойство 4'. Плоскости, проходящие через ребра трехгранного угла и
биссектрисы противоположных граней пересекаются по одной прямой.
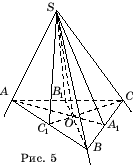
Доказательство. Рассмотрим трехгранный угол SABC, SA = SB = SC (рис.
5). Тогда биссектрисы SA1, SB1, SC1 углов
BSC, ASC, ASB являются
медианами соответствующих треугольников. Поэтому AA1,
BB1, CC1–
медианы треугольника ABC. Пусть O – точка их пересечения. Прямая SO
содержится во всех трех рассматриваемых плоскостях и, следовательно, является
линией их пересечения.
Свойство 5. Высоты треугольника
пересекаются в одной точке.
Свойство 5'. Плоскости, проходящие через ребра трехгранного угла
и перпендикулярные противоположным граням, пересекаются по одной прямой.
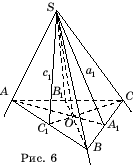
Доказательство. Рассмотрим трехгранный угол с вершиной S и
ребрами a, b, c. Обозначим a1, b1, c1–
линии пересечения граней с плоскостями, проходящими через соответствующие ребра
и перпендикулярные этим граням (рис. 6). Зафиксируем точку C на ребре c
и опустим из нее перпендикуляры CA1 и CB1 на прямые a1 и b1.
Обозначим A и B пересечения
прямых CA1 и CB1 с прямыми a и b. Тогда SA1
является проекцией AA1
на грань BSC. Так как BC
перпендикулярна SA1, то
она перпендикулярна и AA1. Аналогично, AC перпендикулярна BB1. Таким образом, AA1 и BB1 являются высотами треугольника ABC. Пусть O
– точка их пересечения. Плоскости, проходящие через прямые a и a1, b и b1
перпендикулярны плоскости ABC и,
следовательно, линия их пересечения SO перпендикулярна ABC.
Значит, SO перпендикулярна AB. С другой стороны, CO перпендикулярна
AB. Поэтому плоскость, проходящая через ребро c и SO будет
перпендикулярна противоположной грани.
Свойство 6 (теорема
синусов). В треугольнике ABC со
сторонами a, b, c соответственно, имеют место равенства a
: sin A = b : sin B = c : sin
C.
Свойство 6'. Пусть a, b , g - плоские углы трехгранного угла, a, b, c – противолежащие им
двугранные углы. Тогда sin a : sin a = sin b : sin b =
sin g : sin c.
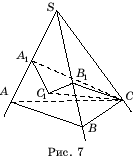
Доказательство.Пусть SABC –
трехгранный угол. Опустим из точки C перпендикуляр CC1
на плоскость ASB и перпендикуляр CA1
на ребро SA (рис. 7). Тогда угол CA1C1
будет линейным углом двугранного угла a. Поэтому CC1
= CA1sin a = SCsin bsin a. Аналогично
показывается, что CC1 = CB1sin b = SCsin asin b.
Следовательно, имеет место равенство sin b sin a = sin a sin b и, значит,
равенство sin a: sin a = sin b : sin b.
Аналогичным образом доказывается, что имеет место равенство sin b: sin b = sin g : sin c.
Свойство 7. Если
в выпуклый четырехугольник можно вписать окружность, то суммы противоположных
сторон равны.
Свойство 7'. Если в выпуклый четырехгранный угол
можно вписать сферу, то суммы противоположных плоских углов равны.
Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз,
1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в
пространстве. – М.-Л.: Гостехиздат, 1949.
3. Энциклопедия элементарной математики. Книга IV. Геометрия. - М.; 1963.
4. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
