ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА МАКСИМУМ И МИНИМУМ

 

Обычно экстремальные задачи, или задачи на нахождение наибольших и наименьших значений, решаются в курсе алгебры и начал анализа старших классов с помощью производной. 

Вместе с тем, имеется важный класс геометрических экстремальных задач, которые решаются своими методами без помощи производной.

Эти задачи, с одной стороны, имеют большое значение, как для математики, так и для ее приложений, а с другой стороны, могут служить пропедевтикой изучения соответствующих разделов курса алгебры и начал анализа.

Здесь мы рассмотрим некоторые классические экстремальные задачи по геометрии

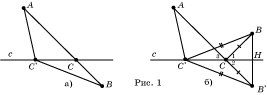
Задача 1. Дана прямая с и две точки А и В, не лежащие на этой прямой. Требуется найти такую точку С на прямой c, чтобы сумма расстояний АС + СВ была наименьшей.

Решение. Рассмотрим сначала случай, когда точки A и B лежат по разные стороны от прямой c (рис. 1,а). Легко видеть, что в этом случае искомой точкой C является точка пересечения отрезка AB и прямой c. Учащимся можно предложить самостоятельно доказать, что для любой другой точки C’ прямой c будет выполняться неравенство AC + CB < AC’ + C’B и, следовательно, сумма AC + CB будет  наименьшей. Доказательство непосредственно следует из неравенства треугольника.

Пусть теперь точки A и B лежат по одну сторону от прямой c (рис. 1,б). Идея нахождения искомой точки C состоит в замене точки B на точку B’, лежащую по другую сторону от прямой c, и сведению этого случая к предыдущему.

Из точки В опустим на прямую с перпендикуляр ВН и отло­жим отрезок НВ', равный ВН (рис. 1,б). Прямая c будет серединным перпендикуляром к отрезку BB’ и, следовательно, для произвольной точки С’ на прямой с будет выполняться равенство С’В = С’В'. По­этому сумма АС’ + С’В будет наименьшей тогда и только тогда, когда наи­меньшей будет равная ей сумма АС’ + С’В'. Ясно, что последняя сумма является наи­меньшей в случае, если точки А, В', С’ лежат на одной прямой, т.е. ис­комая точка С является точкой пересечения отрезка АВ' с прямой с.

Полученная точка С обладает тем свойством, что углы, образованные прямыми АС и СВ и прямой с, равны. Действительно, 1 = 2, как соответствующие углы в равных треугольниках BHC и B’HC, 2 = 3, как вертикальные углы. Следовательно, 1 = 3.

Из этого равенства можно вывести закон отражения света. А именно, известно, что луч света распространяется по кратчайшему пути. Поэтому, если луч света исходит из точки A, отражается от прямой c и приходит в точку B, то точка C будет точкой отражения и, таким образом, имеет место закон отражения света: угол падения светового лу­ча равен углу отражения.

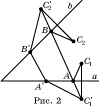
Задача 2. Внутри угла со сторонами a и b даны точки C₁ и C₂. Требуется найти такие точки A и B на сторонах этого угла, чтобы длина ломаной C₁ABC₂ была наименьшей.

Решение. Метод решения этой задачи аналогичен предыдущему. А именно, обозначим через C₁’, C₂’ точки симметричные точкам C₁, C₂ соответственно, относительно прямых a, b (рис. 2). Пусть A и B – точки пересечения прямой C₁’C₂’ со сторонами угла. Тогда C₁A + AB + BC₂ = C₁’A + AB + BC₂’ = C₁’C₂’. Для любых других точек A’, B’ на сторонах угла имеем: C₁A’ + A’B’ + B’C₂ = C₁’A’ + A’B’ + B’C₂’ > C₁’C₂’. Последнее неравенство выполняется так как длина ломаной больше длины отрезка, соединяющего ее концы. Поэтому точки A и B являются искомыми точками, для которых длина соответствующей ломаной наименьшая.

Задача 3. Внутри угла со сторонами a и b дана точка C. Требуется найти такие точки A и B на сторонах этого угла, чтобы периметр треугольника ABC был наименьшим.

Ясно, что эта задача получается из предыдущей, если положить C₁ = C₂ = C. Построение соответствующих точек A и B можно предложить учащимся в качестве самостоятельной работы. Решение показано на рисунке 3,а, в котором точки C’, C” симметричны точке C относительно прямых a, b соответственно.

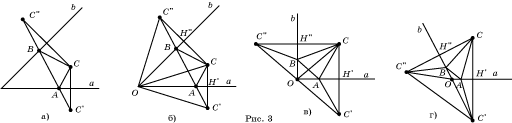
Рассмотрим вопрос о том, в каком случае существует решение этой и предыдущей задач.

Дело в том, что прямая C’C” может не пересекать стороны угла. Выясним в каких случаях это может происходить.

Обозначим через O вершину угла и соединим ее отрезками с точками A, B и C (рис. 3,б). Тогда C’OH’ = COH’, C”OH” = COH” и, следовательно, C’OC” = 2H’OH”.

Если данный угол острый, то угол C’OC” меньше развернутого и, следовательно, прямая C’C” пересекает стороны угла и, значит, задача имеет решение.

Если данный угол прямой, то угол C’OC” – развернутый и, следовательно, прямая C’C” проходит через вершину O угла. В этом случае задача 3 не имеет решения. Какие бы точки A и B на сторонах угла мы не взяли существуют точки A’, B’, для которых периметр соответствующего треугольника меньше (рис. 3,в).

Если данный угол тупой, то угол C’OC” – больше развернутого и, следовательно, прямая C’C” не имеет общих точек со сторонами угла. В этом случае задача 3 также не имеет решения. Какие бы точки A и B на сторонах угла мы не взяли существуют точки A’, B’, для которых периметр соответствующего треугольника меньше (рис. 3,в).

В качестве самостоятельной работы предлагаем провести аналогичное исследование задачи 2.

Задача 4. В данный треугольник вписать треугольник наименьшего периметра.

Решение. Пусть ABC – данный треугольник. На его сторонах требуется найти такие точки D, E, F, для которых периметр треугольника DEF был бы наименьшим.

Зафиксируем сначала точку D и будем искать точки E и F, для которых периметр треугольника DEF наименьший (при данном положении точки D).

Эта задача аналогична задаче 3. Поэтому для нахождения точек E и F нужно рассмотреть точки D’ и D” симметричные точке D относительно прямых AC и BC, провести прямую D’D” (рис. 4). Искомыми точками E и F будут точки пересечения этой прямой со сторонами AC и BC треугольника ABC.

Будем предполагать, что треугольник ABC остроугольный. Тогда такие точки будут существовать.

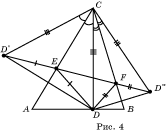
Будем теперь менять положение точки D, и искать такое положение, при котором периметр соответствующего треугольника DEF наименьший. Для этого рассмотрим треугольник D’D”C. Учащимся можно предложить самим указать свойства этого треугольника.

Так как D’C симметрична DC относительно AC, то D’E = DE, D’C = DC и D’CA =DCA. Аналогично, D”F = DF, D”C = DC и D”CB = DCB. Следовательно, треугольник D’D”C равнобедренный. Его боковая сторона равна CD. Основание D’D” равно периметру p треугольника DEF. Угол D’CD” равен удвоенному углу ACB треугольника ABC и, значит, не зависит от положения точки D.

В равнобедренном треугольнике с данным углом при вершине основание тем меньше, чем меньше боковая сторона. Поэтому наименьшее значение периметра p достигается в случае наименьшего значения CD. Это значение принимается в случае, если CD является высотой треугольника ABC. Таким образом, искомой точкой D на стороне AB является основание высоты, проведенной из вершины C.

Заметим, что мы могли бы фиксировать сначала не точку D, а точку E или точку F и получили бы, что E и F являются основаниями соответствующих высот треугольника ABC.

Из этого следует, что искомым треугольником DEF, наименьшего периметра, вписанным в данный треугольник ABC является треугольник, вершинами которого служат основания высот треугольника ABC.

В качестве самостоятельной работы предлагаем доказать, что в случае прямоугольного или тупоугольного треугольника задача не имеет решения.

Рассмотрим теперь задачу Штейнера, имеющую большое прикладное значение, связанное с прокладкой дорог, трубопроводов и т.д., соединяющих заданные пункты и имеющих наименьшую протяженность.

Задача 5. Для данного треугольника найдите точку, сумма расстояний от которой до вершин треугольника принимает наименьшее значение.

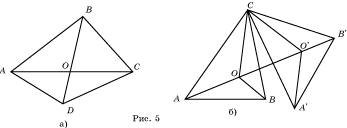
Заметим, что аналогичная задача для четырехугольника ABCD решается довольно просто (рис. 5,а). Искомой точкой O, для которой сумма расстояний наименьшая, является точка пересечения диагоналей этого четырехугольника. Действительно, OA + OB + OC + OD = OA + OC + OB + OD. Сумма первых двух слагаемых принимает наименьшее значение, в случае, если точки A, O, B лежат на одной прямой. Аналогично, точки B, O, D также должны лежать на одной прямой и, значит, O – точка пересечения диагоналей.

Конечно, на практике приходится иметь дело с большим количеством точек, и решение таких задач использует компьютеры. В случае трех точек имеется элементарное решение.

Прежде чем непосредственно перейти к решению задачи Штейнера рассмотрим одну из замечательных точек треугольника, связанную с задачей Штейнера – точку Торричелли.

Точкой Торричелли треугольника ABC называется такая точка O, из которой стороны данного треугольника видны под углом 120, рис. 6,а, т.е. углы AOB, AOC и BOC равны 120.

Докажем, что в случае, если все углы треугольника меньше 120, то точка Торричелли существует.

Выясним, что является геометрическим местом точек, из которых данный отрезок виден под углом 120. К этому времени учащиеся должны знать, что геометрическим местом точек, из которых данный отрезок виден под данным углом, является дуга окружности.

Для построения соответствующей дуги окружности на стороне AB треугольника ABC построим равносторонний треугольник ABC’, рис. 6,а, и опишем около него окружность. Отрезок AB стягивает дугу этой окружности величиной 120. Следовательно, точки этой дуги, отличные от A и B, обладают тем свойством, что отрезок AB виден из них под углом 120.

Аналогичным образом, на стороне AC треугольника ABC построим равносторонний треугольник ACB’, рис. 6,а, и опишем около него окружность. Точки соответствующей дуги, отличные A и C, обладают тем свойством, что отрезок AC виден из них под углом 120.

В случае, если углы треугольника меньше 120, то эти дуги пересекаются в некоторой внутренней точке O. В этом случае AOB = 120, AOC = 120. Следовательно, BOC = 120. Поэтому точка O является искомой.

В случае, если угол A равен 120, то точкой пересечения дуг окружностей будет точка A, рис. 6,б. В этом случае точки Торричелли не существует, так как нельзя говорить об углах, под которыми видны из этой точки стороны AB и AC.

В случае, если угол A больше 120, рис. 6,в, то соответствующие дуги окружностей не пересекаются. Сами окружности пересекаются в некоторой точке O, из которой стороны AB и AC видны под углом 60. В этом случае точки Торричелли также не существует.

Таким образом, во всех трех случаях окружности, описанные около равносторонних треугольников, построенных на сторонах данного треугольника, пересекаются в одной точке. Если углы треугольника меньше 120, то эта точка лежит внутри треугольника и является точкой Торричелли.

Решение задачи Штейнера. Докажем, что в случае, если углы треугольника меньше 120, то искомой точкой в задаче Штейнера является точка Торричелли.

Повернем треугольник ABC вокруг вершины C на угол 60, рис. 5,б. Получим треугольник A’B’C. Возьмем произвольную точку O в треугольнике ABC . При повороте она перейдет в какую-то точку O’. Учащимся можно предложить вопрос о том, какими свойствами обладает треугольник OO’C? Он равносторонний, так как CO = CO’ и OCO’ = 60, следовательно, OC = OO’. Поэтому сумма длин OA + OB + OC будет равна длине ломаной AO + OO’ + O’B’. Ясно, что наименьшее значение длина этой ломаной принимает в случае, если точки A, O, O’, B’ лежат на одной прямой.

Докажем, что это так в случае, если O – точка Торричелли. Действительно,    AOC = 120, COO' = 60. Следовательно, точки A, O, O’ лежат на одной прямой. Аналогично, CO’O = 60, CO'B' = 120. Следовательно, точки O, O’, B’ лежат на одной прямой. Значит, все точки A, O, O’, B’ лежат на одной прямой.

В качестве самостоятельной работы предлагаем доказать, что в случае, если один из углов треугольника больше или равен 120, то решением задачи Штейнера является вершина этого угла.

Рассмотрим еще одну важную задачу, называемую изопериметрической задачей, или задачей Дидоны.

Задача 6. Среди всех простых замкнутых кривых, данной длины найти кривую, ограничивающую фигуру наибольшей площади.

Изопериметрической эта задача называется в связи с постоянством длины кривой, или, что то же самое, периметра искомой фигуры. С именем Дидоны она связывается по легенде, согласно которой финикийская царевна Дидона в IX веке до н. э., спасаясь от преследователей, заключила договор на покупку земли на побережье нынешнего Тунисского залива Средиземного моря с местным предводителем Ярбом. Она попросила совсем немного земли – столько, сколько можно «окружить бычьей шкурой». Сделка состоялась, и тогда Дидона разрезала шкуру быка на тонкие тесемки, связала из них веревку, окружила ей довольно большую территорию и основала на ней крепость, в которой и спасалась от преследователей.

Вопрос состоял в том, какую форму должна иметь территория ограниченная веревкой, чтобы ее площадь была наибольшей?

Заметим, что это не совсем тот вопрос, который мы сформулировали в задаче 6. Действительно, в задаче Дидоны веревка не замкнута, ее концы выходят на берег моря. Мы же рассматриваем замкнутые кривые.

 Хотя решение задачи о нахождении замкнутой кривой, охватывающей наибольшую площадь было известно еще до н.э., строгое его доказательство было дано лишь в конце XIX века. До этого в 30-х годах XIX века Якоб Штейнер дал пять доказательств, но в каждом из них подразумевалось существование такой кривой. Мы рассмотрим первое из доказательств Штейнера. Доказательство существования выходит за рамки кур­са элементарной математики.

Теорема. Среди простых замкнутых кривых заданной длины наибольшую площадь охватывает окружность.

Доказательство разобьем на несколько этапов. Для краткости фигуру, ограниченную кривой, данной длины, имеющую наибольшую площадь, будем называть максимальной.

Теорема 1. Максимальная фигура является выпуклой.

Доказательство будем вести от противного. Предположим, что фигура Ф невыпукла. Тогда существует хорда АВ, концы которой лежат на кривой, а внутренние ее точки - вне кривой, рис. 7,а. Вопрос состоит в том, чтобы найти фигуру Ф’ с тем же периметром, но большей площади. Тем самым будет показано, что фигура Ф не является максимальной.

Заменим дугу исходной кривой, соединяющую точки А, В, на сим­метричную ей дугу относительно прямой АВ. Соответствующая ей фигура Ф’ будет ограничена кривой той же длины, но будет иметь большую площадь по сравнению с исходной. Следовательно, исходная фигура не максималь­ная.

Теорема 2. Если хорда делит кривую, ограничивающую максимальную фигуру на две части равной длины, то она и фигуру делит на две равновеликие час­ти.

Доказательство. Пусть хорда АВ делит кривую на две части равной длины, рис. 7,б. Предположим, что площади образовавшихся частей Ф₁, Ф₂ фигуры Ф не равны, например, S(Ф₁) > S(Ф₂). Построим фигуру Ф’ того же самого периметра, но большей площади. Для этого в фигуре Ф заменим фигуру Ф₂ на фигуру, симметричную Ф₁ относительно прямой АВ. Получен­ная фигура Ф’ будет ограничена кривой той же длины, но будет иметь боль­шую площадь по сравнению с исходной. Следовательно, исходная фигура не максимальная.

Теорема 3. Максимальная фигура ограничена окружностью.

Доказательство. Пусть хорда АВ делит кривую, ограничивающую макси­мальную фигуру Ф на две части равной длины, рис. 7,в. Тогда она делит фигуру Ф на две части равной площади. Если кривая не окруж­ность, то на ней найдется точка С, для которой АСВ  90^о. Предположим, например, что точка C принадлежит верхней части фигуры Ф. Построим новую фигуру Ф’. Для этого рассмотрим прямоугольный треугольник А’В’С’ с прямым углом С’, у которого А’В’ = АВ, В’С’ = ВС. Площадь треугольника А’В’С’ больше площади треугольника ABC. Действительно, площадь треугольника равна половине произведения двух его сторон на синус угла между ними, а синус принимает наибольшее значение, равное единице, если угол равен 90. Для остальных углов больших 0 и меньших 180 синус меньше единицы.

Присоединим к катетам треугольника А’В’С’ соответствующие части Ф₁’ и Ф₂’, равные соответственно частям Ф₁ и Ф₂ исходной фигуры (рис. 7,г). Полученную фигуру отразим симметрично относительно А’В’.  Фигура Ф’, состоящая из обеих этих частей будет искомой. Ясно, что она ограничена кривой той же длины. Однако, т.к. площадь треугольника А’В’С’ больше площади треугольника АВС, то площадь верхней части фигуры Ф’ будет больше площади верхней части фигуры Ф. Аналогично, площадь нижней части фигуры Ф’ будет больше площади нижней части фигуры Ф. Таким образом, площадь всей фигуры Ф’ будет больше площади исходной фигуры Ф. Следовательно, исходная фигура не максимальна.

Что и завершает доказательство теоремы.

 

Литература

1. Энциклопедия элементарной математики. Книга V. Геометрия. – М.: Наука, 1966, с.307.

2. Зетель С.И. Задачи на максимум и минимум. – М.: ОГИЗ Гостехиздат, 1948.

3. Курант Р., Роббинс Г. Что такое математика? . 2-е изд. – М.: Просвещение, 1967, с.362.

4. Нагибин Ф.Ф. Экстремумы. – М.: Просвещение, 1966, с.56.

5. Натансон И.П. Простейшие задачи на максимум и минимум. – М. – Л.: Гос. Изд. технико-теоретический литературы, 1950 /Популярные лекции по математике, выпуск 2.

6. Протасов В.Ю. Максимумы и минимумы в геометрии. М.: МЦНМО, 2005.

7. Тихомиров В.М. Рассказы о максимумам и минимумах. – М.: Наука, 1986 /Библиотечка «Квант», выпуск 56, с.7, с.13 – задачи Герона и Дидоны к первому параграфу.

8. Смирнова И.М., Смирнов В.А.. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005.