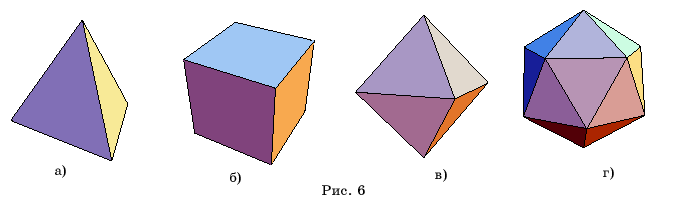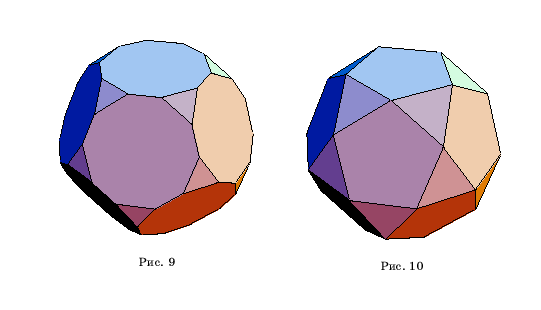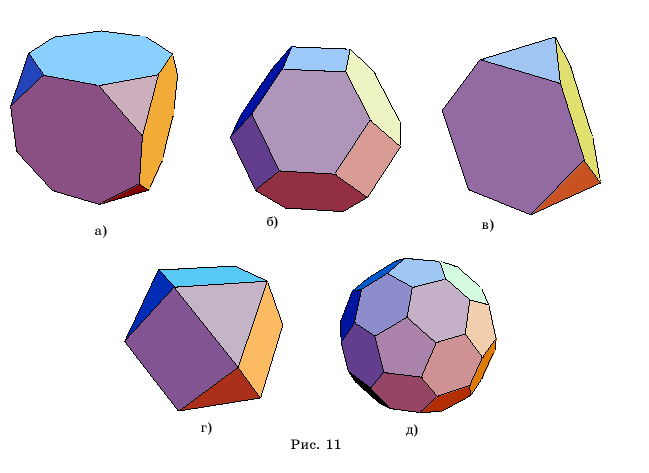КОМПЬЮТЕРНАЯ СИСТЕМА
"MATHEMATICA"
Одним из
существенных препятствий для успешного изучения пространственных фигур
является ограниченность средств их изображения и показа. Так, например,
при определенном навыке можно нарисовать на доске пирамиду, параллелепипед,
призму и даже правильные многогранники. Хотя, получающиеся при этом рисунки,
как правило, далеки от совершенства. Нарисовать же полуправильные и звездчатые
многогранники вообще не представляется возможным. Решить эту проблему может
использование компьютерной программы "Математика",
которая позволяет легко получать изображения на экране монитора различных
пространственных фигур.
Рассмотрим
сначала вопрос об изображении правильных многогранников. В качестве примера
возьмем додекаэдр. Для получения изображения додекаэдра после того, как
вы вошли в программу, нужно набрать
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[p]
После этого
следует нажать клавиши SHIFT и ENTER.
В результате на экране появится цветное изображение додекаэдра, заключенного
в каркасный куб (рис. 1).
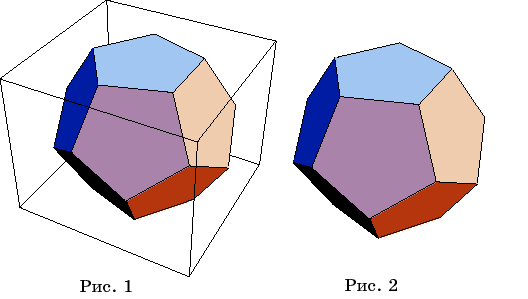 Если вы хотите
убрать куб, то к команде, которую вы набрали, следует добавить
Boxed->False
В результате получится команда
<<Graphics`Polyhedra`
Если вы хотите
убрать куб, то к команде, которую вы набрали, следует добавить
Boxed->False
В результате получится команда
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[p,Boxed->False]
Нажатие клавиш SHIFT
и
ENTER приводит к исполнению этой команды. На экране получим изображение
додекаэдра (рис. 2).
Изображение
додекаэдра можно увеличивать и уменьшать. Для этого нужно щелкнуть по додекаэдру
левой кнопкой мыши. Появится квадрат, содержащий додекаэдр. Подвести курсор
к одному из углов квадрата. Он превратится в наклонную стрелку. Нажав левую
кнопку мыши, перемещайте эту стрелку. При этом квадрат вместе с додекаэдром
будет увеличиваться или уменьшаться в зависимости от направления перемещения.
Достигнув нужных размеров, отпустите кнопку мыши и щелкните ей вне квадрата.
Останется один додекаэдр.
Изображение
додекаэдра можно поворачивать, задавая координаты точки, из которой мы
смотрим на додекаэдр. По умолчанию предполагается точка с координатами
(1.3,-2.4,2). Если вы хотите указать другую точку, то к набранной команде
следует добавить, например,
ViewPoint->{0.8,-2.4,2}
В результате получим команду
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[p,Boxed->False,ViewPoint->{0.8,-2.4,2}]
исполнение которой приводит
к рисунку 3. Команда
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[p,Boxed->False,ViewPoint->{0.8,-2.4,1}]
приведет к рисунку 4.
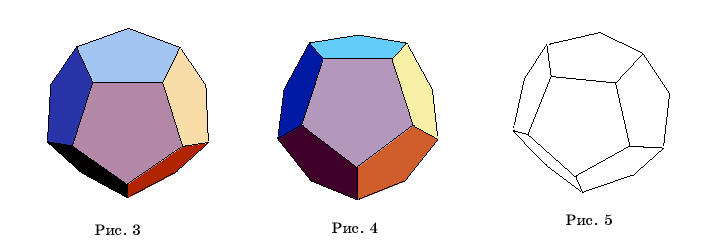 Для устранения
окраски граней додекаэдра следует добавить
Shading->False
В результате получим команду
<<Graphics`Polyhedra`
Для устранения
окраски граней додекаэдра следует добавить
Shading->False
В результате получим команду
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[p,Boxed->False,Shading->False]
исполнение которой приведет
к рисунку 5.
Если
вместо Dodecahedron
написать соответственно Tetrahedron, Hexahedron,
Octahedron, Icosahedron, то получим
изображения тетраэдра, куба, октаэдра и икосаэдра (рис. 6,а-г).
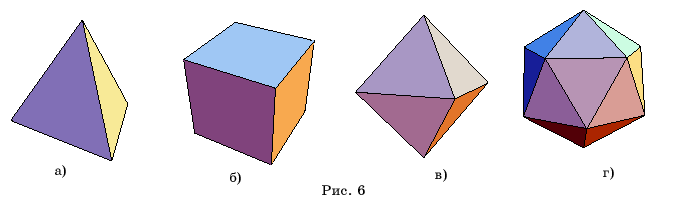 Если вместо
одного многогранника указать несколько многогранников, то получим изображение
многогранника, являющегося объединением указанных многогранников.
Если вместо
одного многогранника указать несколько многогранников, то получим изображение
многогранника, являющегося объединением указанных многогранников.
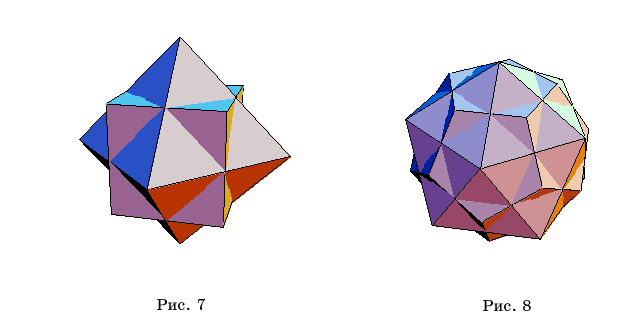
Например,
исполнение команды
<<Graphics`Polyhedra`
p=Polyhedron[Hexahedron]
q=Polyhedron[Octahedron]
Show[{p,q},Boxed->False]
приведет к рисунку 7.
Исполнение
команды
<<Graphics`Polyhedra`
p=Polyhedron[Icosahedron]
q=Polyhedron[Dodecahedron]
Show[{p,q},Boxed->False]
приведет к рисунку 8.
 В программе
"Математика" имеется операция “Truncate”,
при которой от правильных многогранников отсекаются углы и в результате
получаются полуправильные многогранники. Так, например, исполнение команды
<<Graphics`Polyhedra`
В программе
"Математика" имеется операция “Truncate”,
при которой от правильных многогранников отсекаются углы и в результате
получаются полуправильные многогранники. Так, например, исполнение команды
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[Truncate[p],Boxed->False]
приводит к усеченному додекаэдру
(рис. 9).
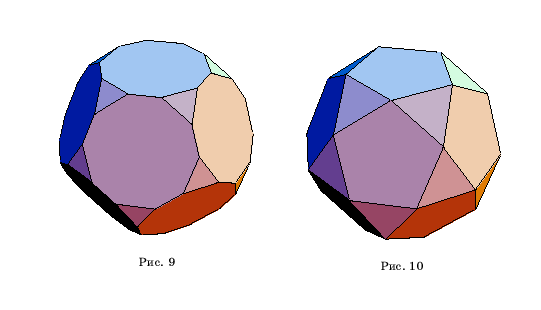 Операцию
усечения можно производить с заданным коэффициентом, показывающим какая
часть ребра отсекается. Так, например, если выбрать коэффициент равным
0.5 , то исполнение соответствующей команды
<<Graphics`Polyhedra`
Операцию
усечения можно производить с заданным коэффициентом, показывающим какая
часть ребра отсекается. Так, например, если выбрать коэффициент равным
0.5 , то исполнение соответствующей команды
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[Truncate[p,0.5],Boxed->False]
приводит к полуправильному многограннику,
называемому икосододекаэдр (рис. 10). Его гранями являются все грани икосаэдра
и все грани додекаэдра.
На рисунке
11,а-д приведены другие примеры многогранников, полученных усечением правильных
многогранников.
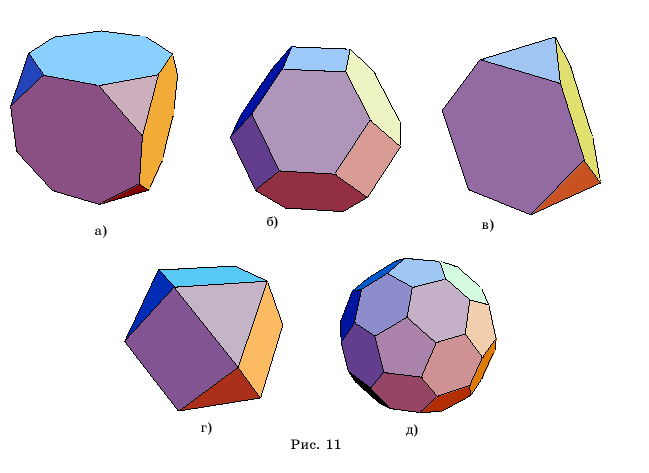 Помимо операции
усечения, в программа "Математика" имеется операция “Stellate”,
которая приводит к звездчатым многогранникам. Так, например, исполнение
команды
<<Graphics`Polyhedra`
Помимо операции
усечения, в программа "Математика" имеется операция “Stellate”,
которая приводит к звездчатым многогранникам. Так, например, исполнение
команды
<<Graphics`Polyhedra`
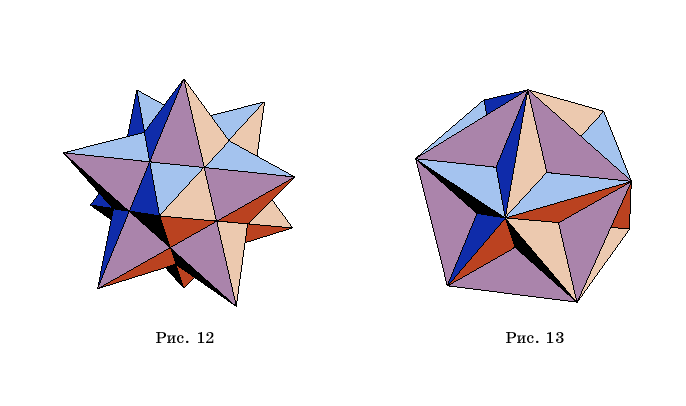
p=Polyhedron[Dodecahedron]
Show[Stellate[p,2.2],Boxed->False]
приводит к многограннику (рис.
12) который называется малым звездчатым додекаэдром.
 Операцию
“Stellate” тоже можно производить с разными коэффициентами. Если коэффициент
меньше единицы, то она производится вовнутрь многогранника. Например, исполнение
команды
<<Graphics`Polyhedra`
Операцию
“Stellate” тоже можно производить с разными коэффициентами. Если коэффициент
меньше единицы, то она производится вовнутрь многогранника. Например, исполнение
команды
<<Graphics`Polyhedra`
p=Polyhedron[Icosahedron]
Show[Stellate[p,0.7],Boxed->False]
приводит к многограннику
(рис.
13), который называется большим додекаэдром.
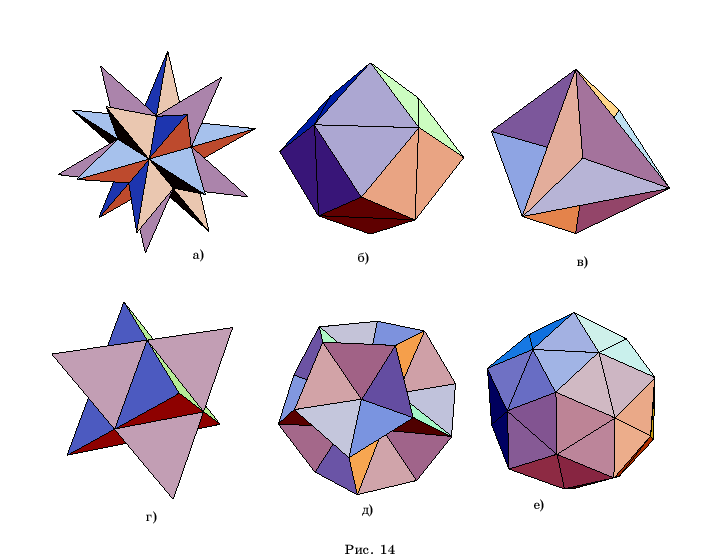
На рисунке
14,а-е, приведены другие примеры многогранников, полученных операцией “Stellate”
из
правильных многогранников.
 Операции
“Truncate”
и
“Stellate”
можно
комбинировать. Например, команда
<<Graphics`Polyhedra`
Операции
“Truncate”
и
“Stellate”
можно
комбинировать. Например, команда
<<Graphics`Polyhedra`
p=Polyhedron[Icosahedron]
Show[Truncate[Stellate[p,0.7],0.5],Boxed->False]
приводит к многограннику (рис.
15).
Команда
<<Graphics`Polyhedra`
p=Polyhedron[Dodecahedron]
Show[Stellate[Stellate[p,2.2],0.5],Boxed->False]
приводит к многограннику (рис.
16), который называется большим икосаэдром.
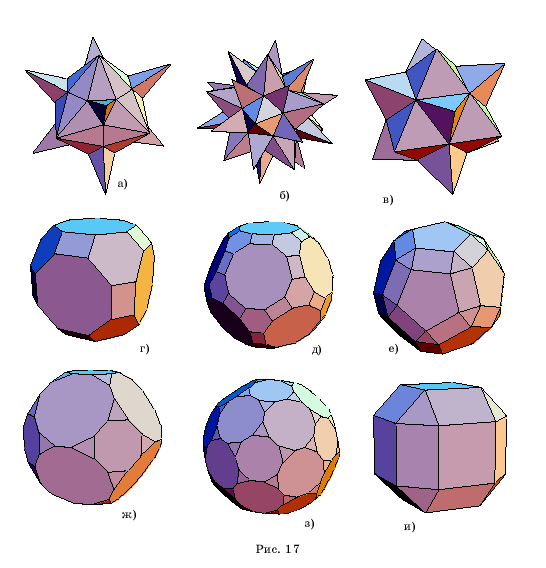
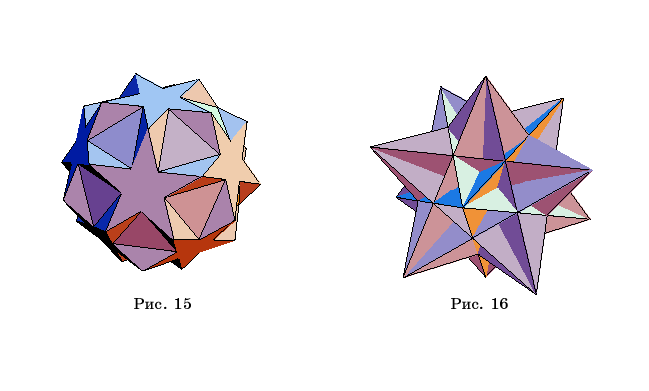 На рисунке
17,а-и, приведены другие примеры многогранников, полученных операцией “Stellate”
и “Truncate” из правильных многогранников.
На рисунке
17,а-и, приведены другие примеры многогранников, полученных операцией “Stellate”
и “Truncate” из правильных многогранников.
 Рассмотрим
теперь вопрос об изображении поверхностей.
Рассмотрим
теперь вопрос об изображении поверхностей.
Одним
из наиболее простых способов задания поверхности в пространстве является
задание ее графиком функции двух переменных z = f(x,y).
Для получения
изображения графика функции z = f(x,y) после
того, как вы вошли в программу, нужно набрать
Plot3D[f[x,y],{x,min,max},{y,min,max},
BoxRatios->Automatic]
где min,
max обозначают пределы изменения аргументов
x
и
y. Нажать клавиши SHIFT и ENTER. В
результате на экране появится график функции y = f(x,y).
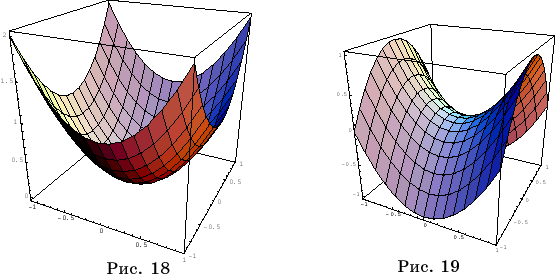
Например,
Plot3D[x^2+y^2,{x,-1,1}, {y,-1,1},BoxRatios->Automatic]
даст график функции z
= x2+y2,
-1 x
x 1,
-1
1,
-1 y
y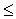 1
(рис. 18).
1
(рис. 18).
Если
вместо x^2+y^2
подставить x^2-y^2, то
получим график функции z = x2-y2
(рис. 19).
 Если перечисленные
выше графики можно нарисовать и без использования компьтерной программы,
то изображение следующих поверхностей требует использование компьютерных
средств. Например,
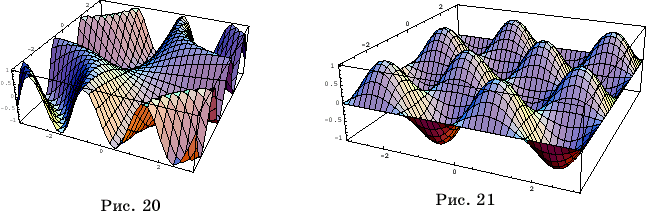
Plot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]
даст график функции z=
sin(xy), -p
Если перечисленные
выше графики можно нарисовать и без использования компьтерной программы,
то изображение следующих поверхностей требует использование компьютерных
средств. Например,
Plot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]
даст график функции z=
sin(xy), -p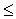 x
x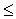 p,
-p
p,
-p y
y p
(рис. 20).
p
(рис. 20).
Если
вместо Sin[x*y]
подставить Sin[x]*Sin[y], то
получим график функции z = sinxsiny
(рис. 21).
 Программа
"Математика" позволяет получать изображения не только поверхностей заданных
уравнением z=f(x,y),
но и поверхностей вращения.
Программа
"Математика" позволяет получать изображения не только поверхностей заданных
уравнением z=f(x,y),
но и поверхностей вращения.
Наиболее
простой такой поверхностью является параболоид вращения, получающийся вращением
графика функции z = x2 вокруг
оси Oz. Для получения поверхности
вращения следует набрать
<<Graphics`SurfaceOfRevolution`
и нажать клавиши SHIFT и ENTER.
Далее набрать
SurfaceOfRevolution[x^2,{x,0,2},BoxRatios->
Automatic,
ViewPoint->{1,-2,1},PlotPoints->30]
и снова нажать SHIFT и ENTER.
Изображение соответствующей поверхность вращения
показано на рисунке 22. Отметим, что это та же самая поверхность, что и
на рисунке 18.
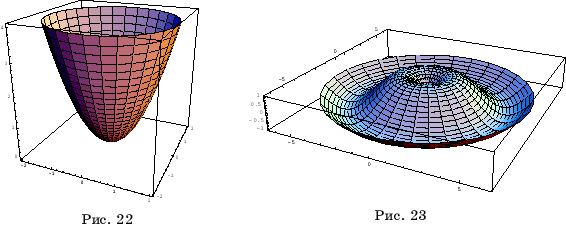 Для получения
поверхности вращения графика функции z=sinx
вокруг оси Oz
следует набрать
<<Graphics`SurfaceOfRevolution`
и нажать клавиши SHIFT и ENTER.
Далее набрать
SurfaceOfRevolution[Sin[x],{x,0,Pi},BoxRatios->
Automatic,
Для получения
поверхности вращения графика функции z=sinx
вокруг оси Oz
следует набрать
<<Graphics`SurfaceOfRevolution`
и нажать клавиши SHIFT и ENTER.
Далее набрать
SurfaceOfRevolution[Sin[x],{x,0,Pi},BoxRatios->
Automatic,
ViewPoint->{1,-2,1},PlotPoints->30];
И снова нажать SHIFT и ENTER.
Изображение соответствующей поверхность вращения
показано на рисунке 23.
Если
вместо Sin[x]
набрать
Exp[x]
и
в качестве пределов изменения x
поставить
{x,-1,1},
то
получится поверхность вращения графика функции z = ex,
(рис.
24).
Если
вместо Sin[x]
подставить 1/x и
пределы изменения x взять
от 0,25 до 2, то получим поверхность
вращения, изображенную на рисунке 25.
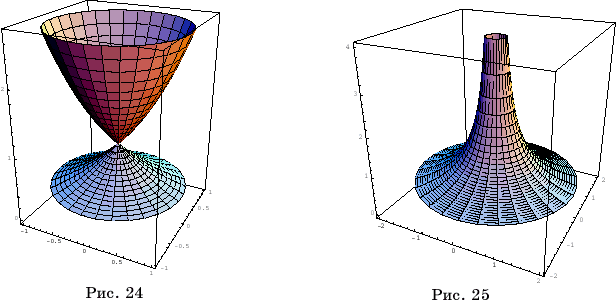 Вращать можно не
только одну, но и несколько кривых. При этом можно отдельно указать ось
вращения. Например, выполнение команды
<<Graphics`SurfaceOfRevolution`
Вращать можно не
только одну, но и несколько кривых. При этом можно отдельно указать ось
вращения. Например, выполнение команды
<<Graphics`SurfaceOfRevolution`
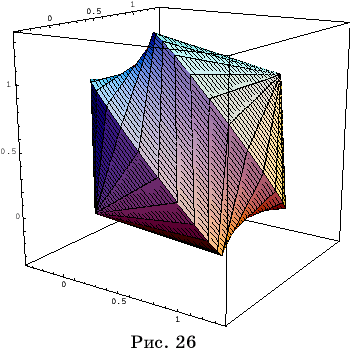
SurfaceOfRevolution[{{1,0,x},{x,0,0},{1,1,x}},
{x,0,1}, RevolutionAxis->{1,1,1},
BoxRatios-> Automatic,
ViewPoint->{2,-3,1},PlotPoints->25]
Приведет к поверхности вращения
куба вокруг его диагонали (рис. 26).
 Некоторые
поверхности программа "Математика" имеет в своей памяти. Так, если набрать
<<Graphics`Shapes`
и нажать клавиши SHIFT и ENTER,
то подгрузится пакет, содержащий некоторые стандартные поверхности.
Некоторые
поверхности программа "Математика" имеет в своей памяти. Так, если набрать
<<Graphics`Shapes`
и нажать клавиши SHIFT и ENTER,
то подгрузится пакет, содержащий некоторые стандартные поверхности.
Если
далее набрать
Show[Graphics3D[Cylinder[]],Boxed->False]
и снова нажать SHIFT и ENTER,
то в результате получим изображение боковой поверхности цилиндра (рис.
27).
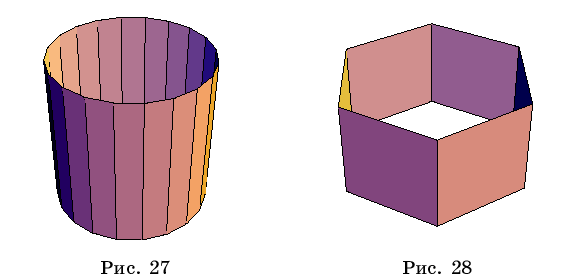 В квадратных
скобках можно указать величину радиуса основания, высоты и числа вершин
многоугольника в основании цилиндра. Например, исполнение команды
Show[Graphics3D[Cylinder[2,1,6]],Boxed->False]
приводит к боковой поверхности
прямой шестиугольной призмы (рис. 28).
В квадратных
скобках можно указать величину радиуса основания, высоты и числа вершин
многоугольника в основании цилиндра. Например, исполнение команды
Show[Graphics3D[Cylinder[2,1,6]],Boxed->False]
приводит к боковой поверхности
прямой шестиугольной призмы (рис. 28).
Если
вместо слова Cylinder
написать
слово Cone,
т.е.
набрать
Show[Graphics3D[Cone[]],Boxed->False]
и снова нажать SHIFT
и ENTER, то в результате получим изображение поверхности конуса (рис. 29).
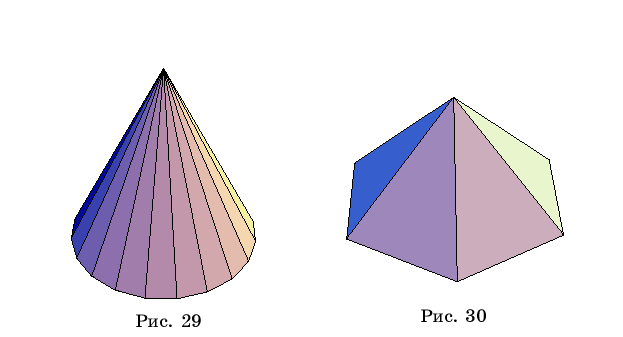 В квадратных
скобках можно указать величину радиуса основания, высоты и числа вершин
многоугольника в основании конуса. Например, исполнение команды
Show[Graphics3D[Cone[2,1,6]],Boxed->False]
приводит к поверхности прямой
шестиугольной пирамиды (рис. 30).
В квадратных
скобках можно указать величину радиуса основания, высоты и числа вершин
многоугольника в основании конуса. Например, исполнение команды
Show[Graphics3D[Cone[2,1,6]],Boxed->False]
приводит к поверхности прямой
шестиугольной пирамиды (рис. 30).
Если
вместо слова Cone
написать
слово Torus,
т.е.
набрать
Show[Graphics3D[Torus[]],Boxed->False]
и снова нажать SHIFT и ENTER,
то в результате получим изображение поверхности тора, поверхности, напоминающей
баранку или бублик (рис. 31).
Если вместо слова Torusнаписать
слово Helix,
т.е.
набрать
Show[Graphics3D[Helix[]],Boxed->False]
и снова нажать SHIFT и ENTER,
то в результате получим изображение поверхности, которая называется геликоидом,
и напоминает винтовую лестницу (рис. 32).
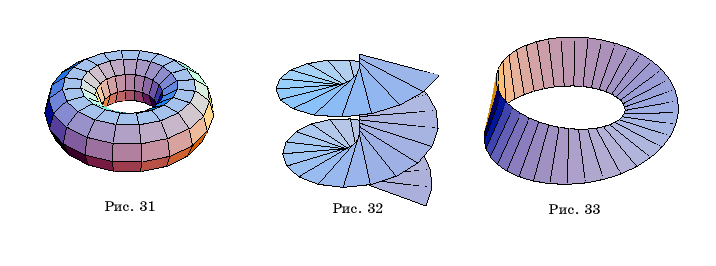 Если вместо
Helix
написать
MoebiusStrip,
то получим изображения листа Мебиуса (рис. 33).
Если вместо
Helix
написать
MoebiusStrip,
то получим изображения листа Мебиуса (рис. 33).
Литература
1. Дьяконов В.П. Системы символьной математики. Mathematica
2 и Mathematica 3. –
М.: СК Пресс, 1998.
2. Смирнова И.М., Смирнов
В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.