КОМПЬЮТЕРНАЯ СИСТЕМА "MAPLE"
    Расссмотрим систему "Maple", которая позволяет легко получать изображения на экране монитора различных пространственных фигур.
    Для получения изображения многогранников после того, как вы открыли окно и вошли в программу, нужно набрать команду
with(geom3d):
и нажать клавишу ENTER. В результате подгружается пакет программ, относящихся к трехмерной графике.
    Затем нужно задать центр многогранника и размеры. Для этого можно набрать
    point(o,0,0,0): r = 1.;
и нажать ENTER. Точка o(0,0,0) будет центром многогранника, r = 1. – радиус описанной сферы.
    Теперь для создания требуемого многогранника нужно набрать его название, например,
dodecahedron(d,o,r);
Буква d является обозначением додекаэдра с центром o и радиусом описанной сферы r.
    Наконец для получения изображения додекаэдра нужно набрать
draw(p);
и нажать Enter. В результате на экране появится цветное изображение додекаэдра (рис. 1). Его можно поворачивать с помощью мышки так, как будто это пространственный объект.
    Цвет многогранника можно менять или убрать его совсем. Для этого в Меню нужно нажать окно Color и выбрать нужную раскраску.
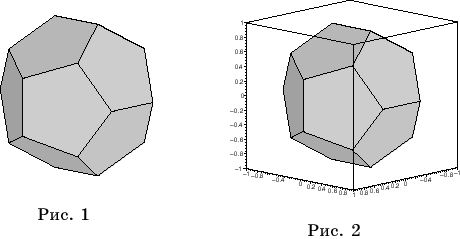    Нажав в Меню окно Axes и выбрав Boxed, можно заключить изображение додекаэдра в координатный куб (рис. 2). Это же можно сделать, написав вместо draw(p); команду draw(p, axes=boxed);
    Изображение многогранника обычно соответствует ортогональному проектированию. Однако можно использовать и центральное проектирование с центром проектирования, расположенным на различном расстоянии от объекта. Для этого в Меню нужно нажать окно Projection и соответственно выбрать: а) Far Perspective; б) Medium Perspective; в) Near Perspective. При этом мы получим изображение, удаленное от объекта: а) далеко; б) на среднем расстоянии; в) близко. Если подобную процедуру мы проделаем с додекаэдром, то получим изображения (рис. 3 - 5). Степень удаленности центра проектирования от объекта можно выбрать, указав соответствующее число от 0 до 1, например, выполнение команды draw(p, projection=0.5); приводит к изображению, удаленному от центра проектирования на среднее расстояние.
    Можно регулировать толщину линий, изображающих ребра многогранника. Для этого нужно нажать на окно Style и в нем Line Width, и после этого выбрать толщину линий. На рисунке 6 линии выбраны толстыми. Это же можно сделать, непосредственно указав толщину линии, например, draw(p, thickness=2);
   
    Если в меню выбрать окно Style и в нем Wireframe, то получим изображение только ребер многогранника (рис. 7). Это же можно получить, выполнив команду draw(p, style=wireframe);
    Если вместо dodecahedron мы напишем: а) tetrahedron; б) hexahedron; в) octahedron; г) icosahedron; то получим изображения соответственно: а) тетраэдра; б) куба; в) октаэдра; г) икосаэдра.
    С этими изображениями можно проводить все операции, рассмотренные выше.
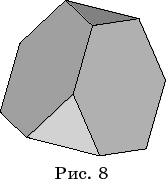
    Для получения изображений полуправильных многогранников нужно вместо названия правильного многогранника написать название полуправильного многогранника. Например, последовательность команд
with(geom3d):
point(o,0,0,0): r = 1.;
TruncatedTetrahedron(p1,o,r);
draw(p1);
приводит к изображению усеченного тетраэдра (рис. 8).
    
    Если вместо названия усеченного тетраэдра написать названия остальных правильных многогранников:
TruncatedHexahedron, TruncatedOctahedron, TruncatedIcosahedron, TruncatedDodecahedron, cuboctahedron, icosidodecahedron, TruncatedCuboctahedron, TruncatedIcosidodecahedron, SmallRhombicuboctahedron, SmallRhombiicosidodecahedron,
то мы получим изображения соответствующих полуправильных многогранников: усеченный куб, усеченный октаэдр, усеченный икосаэдр, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр.
    Для получения изображений звездчатых многогранников нужно в набор команд включить название звездчатого многогранника. Например, последовательность команд
with(geom3d):
point(o,0,0,0): r = 1.;
SmallStellatedDodecahedron(s1,o,r);
draw(s1);
приводит к изображению малого звездчатого додекаэдра (рис. 9).
    Если вместо названия малого звездчатого додекаэдра написать названия остальных правильных звездчатых многогранников:
GreatStellatedDodecahedron, GreatDodecahedron, GreatIcosahedron,
то мы получим изображения правильных звездчатых многогранников: большой звездчатый додекаэдр, большой додекаэдр, большой икосаэдр.
    
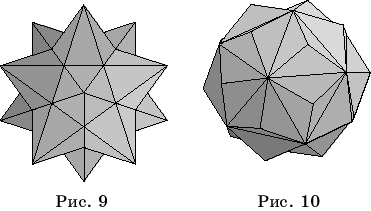    Помимо правильных звездчатых многогранников программа "Maple" позволяет получать изображения большого числа других звездчатых многогранников. Среди них 58 форм звездчатых икосаэдров. Для получения первой звездчатой формы следует набрать
with(geom3d):
point(o,0,0,0): r = 1.;
stellate(si,icosahedron(i,o,r),1);
draw(si);
В результате на экрене появится изображение звездчатого многогранника (рис. 10).
    Если вместо числа 1 в третьей строчке набрать другое число от 1 до 58, то получим изображение соответствующего звездчатого многогранника. На рисунках 11 приведены некоторые изображения.
    
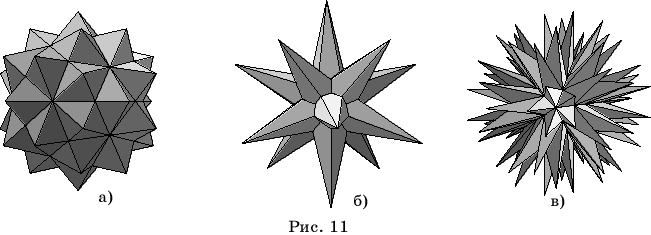    Помимо звездчатых икосаэдров имеются 4 звездчатые формы кубооктаэдра и 18 звездчатых форм икосододекаэдра.
    Для получения первой звездчатой формы кубооктаэдра следует набрать
with(geom3d):
point(o,0,0,0): r = 1.;
stellate(si,cuboctahedron(i,o,r),1);
draw(si);
В результате на экране появится изображение звездчатого многогранника (рис. 12,а).
    Если вместо числа 1 в третьей строчке набрать другое число от 1 до 4, то получим изображение соответствующего звездчатого многогранника. На рисунках 12 приведены соответствующие изображения.
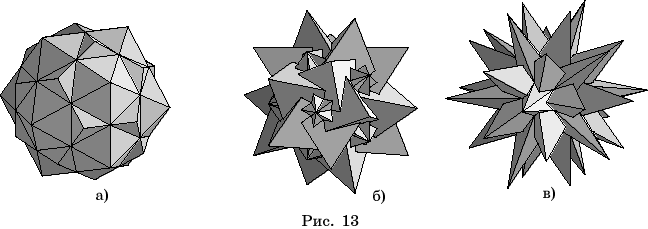
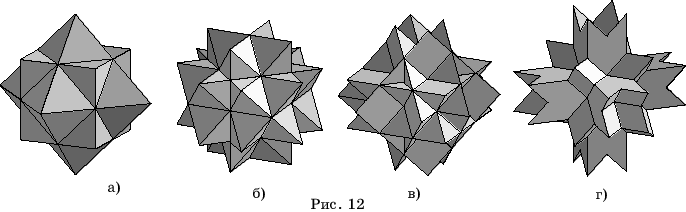    Для получения первой звездчатой формы икосододекаэдра следует набрать
with(geom3d):
point(o,0,0,0): r = 1.;
stellate(si,icosidodecahedron(i,o,r),1);
draw(si);
В результате на экране появится изображение звездчатого многогранника (рис. 13,а).
    Если вместо числа 1 в третьей строчке набрать другое число от 1 до 18, то получим изображение соответствующего звездчатого многогранника. На рисунках 13 приведены некоторые изображения.
    
    Программа "Maple" позволяет получать изображения двойственных многогранников, т.е. таких, центры граней которых являются вершинами исходных многогранников. Например, многогранником, двойственным к кубу, является октаэдр, многогранником, двойственным икосаэдру является додекаэдр.
    На рисунках 14 представлены изображения многогранников, двойственных полуправильным многогранникам, полученные с помощью программы "Maple". Их гранями являются равные (неправильные) многоугольники.
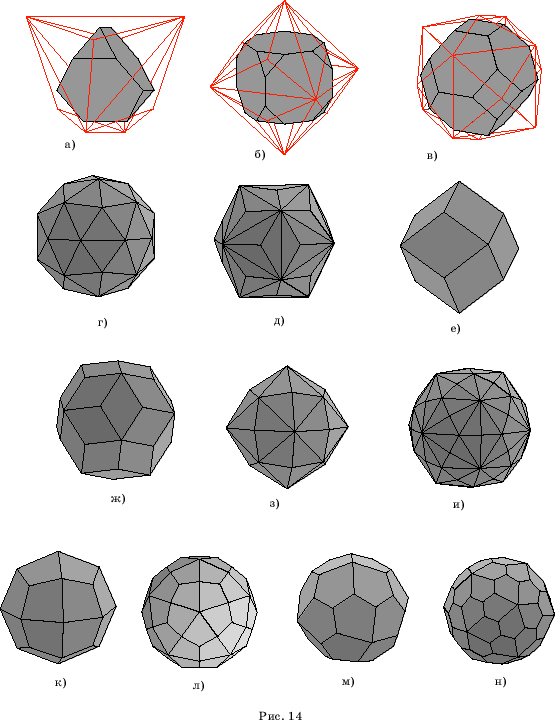    Для получения этих изображений нужно в набор команд включить команду создания двойственного многогранника. Например, для получения изображения многогранника, двойственного к усеченному тетраэдру, вместе с самим усеченным тетраэдром (рис. 14,а) нужно выполнить следующую последовательность команд:
with(geom3d):
point(o,0,0,0): r = 1.;
duality(dp1,TruncatedTetrahedron(p1,o,r),1);
draw([dp1(color=red,style=wireframe),p1(color=green)]);
При этом усеченный тетраэдр будет изображен зеленым цветом, а ребра двойственного многогранника – красным. Если же вместо последней строчки в этих командах мы напишем
draw([dp1,(color=red),p1(color=green)] ,style=wireframe);
то получим изображение реберного зеленого усеченного тетраэдра вместе с описанным около него красным реберным двойственным многогранником.
    Если мы хотим получить изображение одного двойственного многогранника, например, ромбододекаэдра (рис. 14,е) без исходного полуправильного (кубооктаэдра), то нужно выполнить последовательность команд
with(geom3d):
point(o,0,0,0): r = 1.;
duality(dp1,cuboctahedronon(p1,o,r),1);
draw(dp1);

    Литература
1. Дьяконов В. Maple 6. – Санкт-Петербург, 2001.
2. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.

Hosted by uCoz