МАГИЧЕСКИЕ И ГРЕКО-ЛАТИНСКИЕ КВАДРАТЫ

    Упоминание о магических квадратах встречается в китайских книгах еще за 4000 – 5000 лет до нашей эры. В Европе магические квадраты появились лишь в начале XV века. Им приписывались волшебные свойства, они служили талисманами, защищавшими от несчастий.
    Одним из старейших является китайский магический квадрат. В обычной записи он выглядит следующим образом

    Девять порядковых чисел размещены в девяти клетках таким образом, что суммы чисел вдоль каждой строки, каждого столбца и каждой диагонали одинаковы.
    В общем случае магическим квадратом называется такое расположение чисел от 1 до n² в клетках квадратной таблицы nn, при котором суммы чисел в каждой строке, каждом столбце и каждой диагонали одинаковы. Число n называется порядком квадрата, а число s, равное сумме чисел в строках (или столбцах) называется магической суммой.
    Для каждого n магическая сумма s вполне определена. Действительно, так как сумма чисел в каждой строке равна s, а строк – n, то сумма всех чисел магического квадрата равна sn. С другой стороны, сумма всех чисел от 1 до n² равна 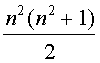. Приравнивая 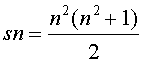, находим .
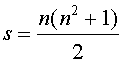    В частности, для рассмотренного выше магического квадрата третьего порядка s = 15.
    Непосредственной проверкой легко убедиться, что магических квадратов второго порядка не существует.
    Рассмотрим вопрос о том, сколько существует различных магических квадратов третьего порядка. При этом два магических квадрата, получающиеся друг из друга движением, будем считать равными.
    Запишем магический квадрат третьего порядка в общем виде

и выясним, какими могут быть эти числа.
    Докажем, что центральное число y₂ должно равняться 5. Для этого просуммируем числа, стоящие во второй строке, втором столбце и обеих диагоналях. В полученную сумму S каждое число, кроме y₂, входит один раз, а само y₂ входит четыре раза. Поэтому, имеем равенство 1 + … + 9 + 3y₂ =4s. Учитывая, что s = 15, получим y₂ = 5.
    Таким образом, магический квадрат третьего порядка должен иметь вид

    Выясним, где в этом квадрате может располагаться число 9. Оно не может стоять в углу

    В этом случае z₃ должно равняться 1, а каждое из чисел x₂, x₃, y₁, z₁должно быть меньше 6. Но у нас осталось только три числа, меньших 6, а именно, 2, 3, 4. Следовательно, число 9 может располагаться только в середине строки или столбца, т.е. магический квадрат можно записать в виде

    Выясним, где в этом квадрате может располагаться число 7. Ясно, что оно не может располагаться в одной строке с числом 9 и в одной строке с числом 1. Следовательно, оно может располагаться только во второй строке, т.е. магический квадрат можно записать в виде

    В одной строке с числом 9 могут находиться только числа 2 и 4. Причем 4 не может находиться в одном столбце с числом 7, т.е. магический квадрат можно записать в виде

    Оставшиеся числа 6 и 8 могут располагаться только как в квадрате

    Таким образом, магический квадрат третьего порядка (с точностью до движения) определен однозначно.
    Рассмотрим теперь магические квадраты четвертого порядка. Они имеют вид

         Их магическая сумма равна 34. Покажем, что сумма чисел, стоящих в центральном квадрате 2x2, равна магической сумме. Действительно, сумма чисел, стоящих в двух диагоналях, двух центральных столбцах и двух центральных строках равна 634. При этом мы посчитали по одному разу числа, стоящие на краю и по три раза – числа центрального квадрата. Обозначим сумму чисел центрального квадрата s. Тогда имеем равенство 634 = 1+…+16 + 2s. Откуда s = 34.

         Из этого, в частности следует, что в любом магическом квадрате сумма чисел, стоящих в его углах, равна магической сумме. Действительно, эту сумму можно представить как сумму чисел двух диагоналей минус сумма чисел центрального квадрата.

Один из магических квадратов изображен на гравюре Альбрехта Дюрера "Меланхолия" (Заставка сайта кафедры). Средние числа в последней строке изображают год 1514, когда была написана эта гравюра.

    Помимо основных, этот магический квадрат имеет еще дополнительные свойства:
    1. Суммы чисел в квадратах второго порядка, примыкающим к вершинам данного квадрата, также равны 34.
    2. Суммы чисел расположенных на двух параллельных маленьких диагоналях (5 + 3 + 14 + 12, 2 + 8 + 9 + 15) равны магической сумме.
    3. Сумма любых двух чисел, симметричных относительно центра, равна 17.
    4. В каждой строке есть пара рядом стоящих чисел, сумма которых 15, и еще пара рядом стоящих чисел, сумма которых 19.
    5. Суммы квадратов чисел в двух крайних строках и двух средних строках попарно равны.
    6. Суммы квадратов чисел в двух крайних столбцах и двух средних столбцах попарно равны.
    Рассмотрим еще один магический квадрат четвертого порядка, называемый совершенным.
 

    В этом квадрате равны суммы чисел, стоящих не только в столбцах, строках и диагоналях, но и ломаных диагоналях. Например, числа 2, 12, 15 и 5, а также 2, 3, 15 и 14 стоят на ломаных диагоналях, которые можно спрямить, поставив рядом два одинаковых квадрата.
    Данный квадрат остается магическим, если его верхнюю строку переместить вниз или, наоборот, нижнюю строку поставить наверх. Аналогично дело обстоит и со столбцами.
    Если из такого квадрата выложить паркет, то в полученном заполнении плоскости  сумма любых четырех чисел, расположенных подряд по вертикали, горизонтали или по диагонали равна магической сумме, а сумма любых двух чисел, расположенных на одной диагонали через одну клетку, равна 17.
    Свернем квадрат в тор, склеив противоположные стороны. Суммы чисел расположенных вдоль меридианов или параллелей этого тора будут равны магической сумме.
    Сопоставим 16 клеток квадрата с 16 вершинами четырехмерного гиперкуба. Сумма чисел, стоящих в вершинах каждой из 24 квадратных граней гиперкуба, равна 34, а суммы пар чисел, расположенных в концах больших диагоналей куба, равны 17.

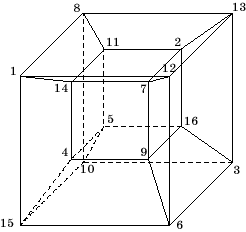
   Общее число различных магических квадратов (с точностью до движений) равно 880. Укажем способ составления таких квадратов. Запишем магический квадрат четвертого порядка в общем виде

где x_i, y_i, z_i, t_i (1i4) – различные числа от 1 до 16.
    Уменьшим каждое число магического квадрата на 1 и заметим, что каждое число от 0 до 15 раскладывается в сумму чисел 1, 2, 4, 8, причем каждое из них участвует в сумме не более одного раза: 1 = 1, 2 = 2, 3 = 1 + 2, 4 = 4, 5 = 1 + 4, 6 = 2 + 4, 7 = 1 + 2 + 4, 8 = 8, 9 = 1 + 8, 10 = 2 + 8, 11 = 1 + 2 + 8, 12 = 4 + 8, 13 = 1 + 4 + 8, 14 = 2 + 4 + 8, 15 = 1 + 2 + 4 + 8.
    Из этого следует, что каждый магический квадрат четвертого порядка может быть разложен в сумму четырех квадратов таких, что в первом будут только единицы, во втором – только двойки, в третьем – только четверки и в четвертом – только восьмерки.
    Так, например, магический квадрат, полученный из квадрата на гравюре А. Дюрера раскладывается в сумму квадратов

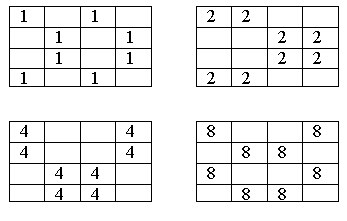
   Заметим, что каждый из полученных квадратов является магическим. В общем случае это не обязательно. Например, магический квадрат

раскладывается в сумму четырех квадратов, два из которых не являются магическими.
    Магический квадрат называется правильным, если каждый из его составляющих квадратов является также магическим квадратом.
    Нетрудно показать, что имеется восемь магических квадратов четвертого порядка, в которых участвуют только два различных числа.

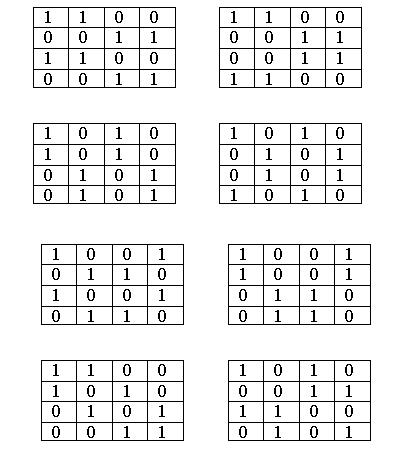
    Складывая эти квадраты по четыре можно получить все правильные магические квадраты четвертого порядка. Непосредственная проверка показывает, что число правильных магических квадратов четвертого порядка равно 11.

Приведем способ составления магических квадратов нечетного порядка на примере квадрата 5-го порядка.

В квадрате 5x5 добавим клетки, как показано на рисунке и впишем в полученную таблицу числа от 1 до 25 подряд по диагоналям

Перенесем числа, не входящие в квадрат 5x5 на 5 клеток соответственно вниз, вверх, вправо или влево так, чтобы они попали на свободное место квадрата. Получим магический квадрат.

    Перейдем теперь к рассмотрению греко-латинских квадратов.
    Латинским квадратом порядка n называется таблица nn, в клетках которой стоят n различных элементов, причем в каждой строке и в каждом столбце каждый элемент участвует только один раз.

"Латинским" этот квадрат называется из-за обозначения элементов латинскими буквами, хотя удобнее обозначать эти элементы натуральными числами от 1 до n.
    Два латинских квадрата порядка n называются ортогональными, если при наложении одного из них на другой каждая из n²упорядоченных пар элементов встретится только один раз. Получившаяся таблица из упорядоченных пар элементов называется эйлеровым или греко-латинским квадратом.

    Последнее название возникло из-за обозначения элементов одного квадрата латинскими буквами, а другого – греческими буквами.
    Способ размещения латинских и греческих букв в указанном выше квадрате дает решение задачи о размещении карт с тузами, королями, дамами и валетами всех четырех мастей в виде квадрата так, чтобы в каждом ряду и каждом столбце квадрата находились карты разных мастей и разных значений.
    Во времена Эйлера были известны греко-латинские квадраты третьего, четвертого и пятого порядков. Вопрос о существовании квадрата шестого порядка Эйлер сформулировал в виде задачи:
    В каждом из шести полков служат шесть офицеров различных званий. Можно ли построить этих 36 офицеров в каре так, чтобы в каждой колонне и каждой шеренге стояли шесть офицеров различных полков и различных званий?
    Эйлер доказал, что существуют греко-латинские квадраты любого нечетного порядка и порядка n, делящегося на 4, и высказал гипотезу о невозможности построения таких квадратов шестого порядка и вообще порядка n = 4k + 2. В 1901 году эта гипотеза была доказана для квадратов шестого порядка. Однако в 1958 году был построен греко-латинский квадрат 10-го порядка, что опровергло гипотезу Эйлера в общем случае.

    Литература
1. Болл У., Коксетер Г. Математические эссе и развлечения. – М.: Мир, 1986.
2. Гарднер Г. Математические досуги. – М.: Мир, 1972.
3. Оре О. Приглашение в теорию чисел. – М.: Наука, 1980.
4. Кордемский Б.А. Математическая смекалка.- М.: Наука, 1991.
5. Постников М.М. Магические квадраты. – М.: Наука, 1964.