КАСКАДЫ ИЗ ПРАВИЛЬНЫХ
МНОГОГРАННИКОВ
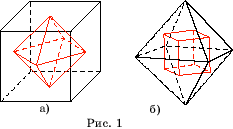
Правильные многогранники можно вписывать
друг в друга. Так, в куб можно вписать октаэдр. Центры граней куба образуют
вершины вписанного в него октаэдра. В свою очередь, центры граней октаэдра
образуют вершины вписанного в него куба. Многогранники, обладающие таким
свойством, называются взаимно двойственными. Таким образом,
октаэдр и куб - взаимно двойственные многогранники (рис. 1, а, б).
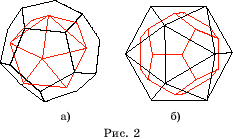
Другим примером взаимно двойственных
правильных многогранников являются додекаэдр и икосаэдр. Центры граней
додекаэдра находятся в вершинах вписанного в него икосаэдра. И наоборот,
центры граней икосаэдра служат вершинами вписанного в него додекаэдра (рис.
2, а, б).
 Правильные
многогранники можно вписывать друг в друга не только таким способом, о
котором сказано выше. Например, в куб можно вписать тетраэдр. При этом
вершины тетраэдра будут лежать в вершинах куба (рис. 3). В свою очередь,
куб можно вписать в додекаэдр так, чтобы вершины куба лежали в вершинах
додекаэдра (рис. 4).
Правильные
многогранники можно вписывать друг в друга не только таким способом, о
котором сказано выше. Например, в куб можно вписать тетраэдр. При этом
вершины тетраэдра будут лежать в вершинах куба (рис. 3). В свою очередь,
куб можно вписать в додекаэдр так, чтобы вершины куба лежали в вершинах
додекаэдра (рис. 4).
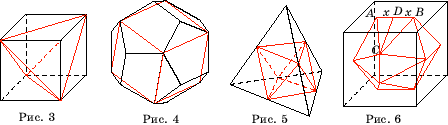 При вписывании
одного правильного многогранника в другой, вершины первого могут лежать
на серединах ребер второго. Такими многогранниками являются тетраэдр и
вписанный в него октаэдр (рис. 5).
При вписывании
одного правильного многогранника в другой, вершины первого могут лежать
на серединах ребер второго. Такими многогранниками являются тетраэдр и
вписанный в него октаэдр (рис. 5).
Есть
и еще один способ: середины ребер вписываемого многогранника лежат в центрах
граней описываемого. А именно, построим на гранях куба отрезки, параллельные
ребрам и середины которых лежат в центрах граней. Одним из таких отрезков
является отрезок AB (рис. 6).
Соединим концы этих отрезков как показано на рисунке 6. В результате получим
многогранник, гранями которого являются двадцать треугольников и в каждой
вершине сходится пять ребер. Для того, чтобы этот многогранник был икосаэдром,
нужно подобрать такую длину отрезка AB,
чтобы все его ребра были равны.
Пусть
ребро куба равно 2. Обозначим длину половины ребра AB
через x. Вычислим
длину ребра BC. На
рисунке 7 изображено сечение куба, перпендикулярное AB
и проходящее через его середину D.
Имеем CD2 = 1 + (1
– x)2 = x2
– 2x + 2. BC2 = BD2
+ CD2 = 2x2
– 2x + 2. Из условия AB
= BC получаем
уравнение 4x2 = 2x2–
2x
+ 2. Откуда находим x = 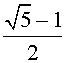 ,
т.
е. x равно золотому отношению.
,
т.
е. x равно золотому отношению.
Аналогичным
образом в куб можно вписать додекаэдр (рис. 8). Правда в этом случае не
все вершины додекаэдра будут лежать на гранях куба.
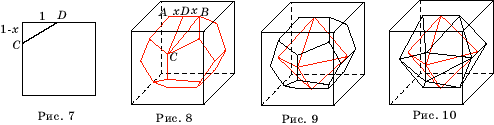 Покажем,
что, комбинируя рассмотренные случаи, в любой правильный многогранник можно
вписать все остальные правильные многогранники.
Покажем,
что, комбинируя рассмотренные случаи, в любой правильный многогранник можно
вписать все остальные правильные многогранники.
Действительно,
как мы говорили, в куб можно вписать октаэдр, тетраэдр, икосаэдр и додекаэдр,
т.е. все остальные правильные многогранники.
В додекаэдр
можно вписать икосаэдр, куб и тетраэдр. Вписывая в куб додекаэдр и октаэдр,
получим октаэдр, вписанный в додекаэдр (рис. 9), и, следовательно, в додекаэдр
можно вписать все остальные правильные многогранники.
В икосаэдр
можно вписать додекаэдр и, следовательно, куб и тетраэдр. Вписывая в куб
икосаэдр и октаэдр, получим октаэдр, вписанный в икосаэдр (рис. 10). Таким
образом, в икосаэдр можно вписать все остальные правильные многогранники.
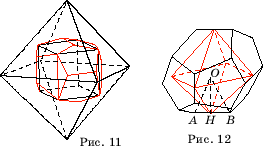
Рассмотрим
октаэдр. В него можно вписать куб и тетраэдр. Описывая около куба, вписанного
в октаэдр, додекаэдр, получим додекаэдр, вписанный в октаэдр (рис. 11).
Аналогично, описывая около куба икосаэдр, получим икосаэдр, вписанный в
октаэдр. Таким образом, в октаэдр можно вписать все остальные правильные
многогранники.
 Рассмотрим
оставшийся правильный многогранник- тетраэдр. В него можно вписать октаэдр.
Вписывая в октаэдр куб, икосаэдр и додекаэдр, получим, что в тетраэдр можно
вписать все остальные правильные многогранники.
Рассмотрим
оставшийся правильный многогранник- тетраэдр. В него можно вписать октаэдр.
Вписывая в октаэдр куб, икосаэдр и додекаэдр, получим, что в тетраэдр можно
вписать все остальные правильные многогранники.
Последовательно
вписывая друг в друга правильные многогранники, получим так называемое
каскадное вписывание. Число всевозможных каскадов из различных правильных
многогранников равно 5!=120.
Сделаем
еще одно замечание, необходимое при построении каскадного вписывания правильных
многогранников. Во-первых, центры последовательно вписанных друг в друга
правильных многогранников совпадают; во-вторых, если вершины вписанного
многогранника лежат в центрах граней описанного многогранника, то радиус
сферы, описанной около вписанного многогранника, будет равен радиусу сферы,
вписанной в описанный многогранник. Если вершины вписанного многогранника
лежат на серединах ребер описанного многогранника, то радиус сферы, описанной
около вписанного многогранника, равен радиусу сферы, касающейся середин
ребер вписанного многогранника.
Поясним
сказанное на примере. Пусть куб вписан в октаэдр. Вершины куба находятся
в центрах граней октаэдра. Обозначим через a6
длину ребра куба,
тогда
R6 = a6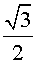 ,
где R6
- радиус сферы, описанной около куба. Пусть теперь R8
- радиус сферы, вписанной в октаэдр, R8
= a8
,
где R6
- радиус сферы, описанной около куба. Пусть теперь R8
- радиус сферы, вписанной в октаэдр, R8
= a8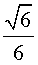 ,
где a8
- длина ребра октаэдра. В нашем случае R6=R8,
т.е. a6
,
где a8
- длина ребра октаэдра. В нашем случае R6=R8,
т.е. a6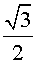 = a8
= a8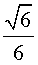 .
.
Следовательно, a8
= 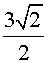 a6,
что позволяет найти ребро октаэдра a8,
описанного около куба с ребром a6.
a6,
что позволяет найти ребро октаэдра a8,
описанного около куба с ребром a6.
В качестве
примера приведем вычисления ребер следующих каскадно вписанных друг в друга
правильных многогранников:
Тетраэдр -> Икосаэдр -> Додекаэдр
-> Октаэдр -> Куб
(a4,r4,R4)
(a20,r20,R20)
(a12,r12,R12)
(a8,r8,R8)
(a6,r6,R6)
Здесь через ai
обозначена длина ребра соответствующего многогранника, через ri
- радиус вписанной сферы, через Ri
- радиус описанной сферы (i=4,
6, 8, 12, 20).
В данном
случае самым внутренним многогранником является куб, а самым внешним -
тетраэдр. Поэтому сначала рассмотрим первый этап: октаэдр 6 куб, т.е. описывание
октаэдра около куба.
Как было
показано выше, длина ребра описанного октаэдра a8
связана с длиной ребра вписанного куба a6
следующим соотношением: 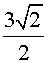 a6=a8.
a6=a8.
Второй
этап: додекаэдр в октаэдр.
Вычислим длину ребра додекаэдра
a12,
описанного около октаэдра. Вершины октаэдра лежат в серединах противоположных
ребер додекаэдра (рис. 12). Следовательно, радиус сферы, описанной около
октаэдра, равен радиусу сферы, касающейся середин ребер додекаэдра. Радиус
этой второй сферы легко найти, рассмотрев треугольник AOB, AB
- ребро додекаэдра, точка O
- центр октаэдра и додекаэдра, OH,
радиус искомой сферы, равен высоте равнобедренного треугольника, опущенной
из вершины O. Так как |AO|=|BO|=R12,
то |OH|=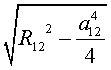 .
Замечая, что R12= a12
.
Замечая, что R12= a12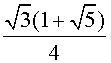 ,
имеем |OH|=
,
имеем |OH|= 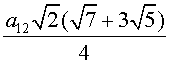 .
.
Далее |OH|=R8,
отсюда 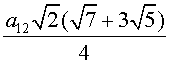 = a8
= a8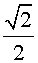 и, следовательно, a12=
и, следовательно, a12=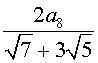 .
.
Третий
этап: икосаэдр в додекаэдр.
Эти многогранники двойственны,
поэтому r20=R12,
т.е. a20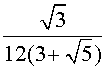 = a12
= a12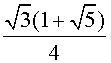 и,
следовательно, a20=
и,
следовательно, a20=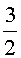 a12(
a12(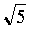 -1).
-1).
Четвертый
этап: тетраэдр в икосаэдр.
Грани икосаэдра лежат на
гранях тетраэдра, причем центры соответствующих граней совпадают, т.е.
равны радиусы вписанных сфер: r4=r20,
тогда a4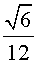 = a20
= a20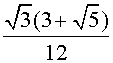 и, следовательно,
и, следовательно,
a4 = 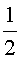 a20
a20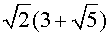 .
После того
как вычислены ребра всех правильных многогранников, участвующий в данном
каскадном вписывании, можно приступать к изготовлению модели. При этом
следует начинать с самого внутреннего многогранника - куба, - и заканчивать
внешним - тетраэдром.
.
После того
как вычислены ребра всех правильных многогранников, участвующий в данном
каскадном вписывании, можно приступать к изготовлению модели. При этом
следует начинать с самого внутреннего многогранника - куба, - и заканчивать
внешним - тетраэдром.
Литература
1. Адамар Ж. Элементарная
геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Баврин И.И., Садчиков
В.А. Новые задачи по стереометрии. – М.: Владос, 2000.
3. Смирнова И.М. Каскады
из правильных многогранников. //Математика в школе. – 1994. - № 3.
4. Смирнова И.М. В мире
многогранников. – М.: Просвещение, 1995.
5. Перепелкин Д.И. Курс
элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат,
1949.
6. Энциклопедия элементарной
математики. Книга IV. Геометрия. - М.; 1963.





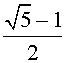 ,
т.
е. x равно золотому отношению.
,
т.
е. x равно золотому отношению.


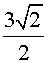 a6,
что позволяет найти ребро октаэдра a8,
описанного около куба с ребром a6.
a6,
что позволяет найти ребро октаэдра a8,
описанного около куба с ребром a6.
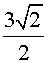 a6=a8.
a6=a8.
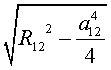 .
Замечая, что R12= a12
.
Замечая, что R12= a12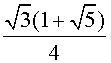 ,
имеем |OH|=
,
имеем |OH|= 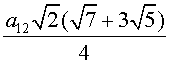 .
.
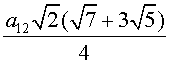 = a8
= a8![]() и, следовательно, a12=
и, следовательно, a12=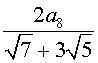 .
.
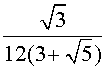 = a12
= a12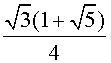 и,
следовательно, a20=
и,
следовательно, a20=![]() a12(
a12(![]() -1).
-1).
![]() = a20
= a20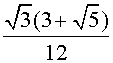 и, следовательно,
и, следовательно,