ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНЫХ
ГРАФИЧЕСКИХ РЕДАКТОРОВ ДЛЯ ИЗОБРАЖЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР.
В школьном
курсе геометрии классов рассматривается
способ построения фигур на плоскости с помощью циркуля и линейки. Показывается,
как построить треугольник по его трем элементам, биссектрису угла, серединный
перпендикуляр, прямую, параллельную данной и т.д. В старших классах изучается
параллельное проектирование и изображение пространственных фигур в параллельной
проекции.
Однако
использование циркуля и линейки для изображения пространственных фигур
имеет свои недостатки:
1. Оно
занимает много времени даже для изображения простых пространственных фигур,
не говоря уже о сложных.
2. Использование
циркуля и линейки является скорее теоретическим методом, свидетельствующим
о возможности построения фигуры, чем практическим. На практике неизбежные
погрешности могут приводить к неправильным изображениям. Например, такие
погрешности возникают при построении прямой параллельной данной и т. п.
3. Для
изображения круглых тел (цилиндр, конус, сфера) требуется построить изображение
окружности, являющееся эллипсом. Однако циркулем и линейкой можно построить
отдельные точки эллипса, но не весь эллипс. Соединяя же отдельные построенные
точки эллипса плавной кривой, мы получим только приближенное изображение
эллипса, не всегда хорошего качества.
Строить
изображения пространственных фигур можно не только с помощью циркуля и
линейки, но и используя компьютерные графические редакторы. Такой способ
изображения пространственных фигур имеет ряд преимуществ по сравнению с
использованием циркуля и линейки:
1. Наличие
в стандартных фигурах графических редакторов правильных многоугольников
и эллипса, легкость построения параллельных прямых, параллелограммов и
др. существенно ускоряет процесс построения, дает возможность изображать
многогранники и круглые тела.
2. Использование
графических редакторов позволяет получать изображения гораздо более сложных
пространственных фигур, в том числе на комбинации многогранников и тел
вращения.
3. Построенные
учениками изображения могут составить компьютерную коллекцию изображений
пространственных фигур, ежегодно пополняемую самими учениками.
Рассмотрим
возможности использования графического редактора “Adobe Illustrator”
для получения изображения плоских и пространственных
фигур.
Для рисования
различных линий служит инструмент Перо, расположенный в окошечке
панели инструментов с изображением пера.
Сначала
выясним, как рисуются прямые линии. В панели инструментов выберите окошечко
с изображением пера, щелкнув по нему левой кнопкой мыши. Затем щелкните
левой кнопкой мыши в каком-нибудь месте экрана там, где вы хотите, чтобы
был один из концов отрезка. Переместите указатель в другое место экрана,
и создайте второй конец отрезка, щелкнув еще раз левой кнопкой. Первая
и вторая точка будут соединены отрезком. Продолжая щелкать левой кнопкой
в различных точках экрана, можно получать различные ломаные линии. Щелкнув
по начальной точке, получим замкнутую ломаную линию.
Для рисования
кривых линий нажмите левую кнопку мыши в каком-нибудь месте экрана и, удерживая
ее нажатой, переместите указатель на небольшое расстояние. В обе стороны
от начальной точки, по направлению перемещения указателя потянется прямая
линия. Назовем ее управляющей. Отпустите кнопку. Управляющая линия зафиксируется.
Нажмите левую кнопку в каком-нибудь другом месте экрана. При этом начальная
и конечная точка соединятся отрезком. Не отпуская кнопку, переместите указатель
на небольшое расстояние. При этом в обе стороны от конечной точки потянется
вторая управляющая линия. Отрезок, соединяющий начальную и конечную точку,
превратится в кривую, для которой управляющие линии будут касательными
в начальной и конечной точках. Меняя направления и величину управляющих
линий можно получать самые разнообразные кривые, соединяющие начальную
и конечную точку. Нажимая левую кнопку в других местах экрана и создавая
новые управляющие линии, можно получать кривые, проходящие через несколько
заданных точек.
Для получения
изображения прямоугольника в панели инструментов выберите окошечко с изображением
прямоугольника, щелкнув по нему левой кнопкой мыши. Поместите указатель
в какое-нибудь место экрана там, где вы хотите, чтобы была вершина прямоугольника.
Нажмите левую кнопку и удерживая ее нажатой перемещайте указатель.
При этом за ним потянется прямоугольник. Достигнув нужного положения, отпустите
кнопку. Произойдет фиксирование прямоугольника с вершинами в начальной
и конечной точке перемещения. Если при перемещении указателя дополнительно
держать нажатой клавишу Shift, то в
результате получится квадрат с вершиной в начальной точке.
Создание
изображений эллипса и окружности производится с помощью окошечка с эллипсом,
и оно совершенно аналогично созданию изображения прямоугольника и квадрата.
Для получения
изображения правильных многоугольников поставьте указатель на окошечко
с изображением эллипса, нажмите левую кнопку мыши и удерживайте ее нажатой.
Откроются новые окошечки с изображениями многоугольника, звездчатого многоугольника
и спирали. Подведите указатель к многоугольнику и отпустите кнопку. При
этом окошечко с изображением эллипса на панели инструментов заменится на
многоугольник. Далее последовательность действий аналогична предыдущему.
А именно, поместите указатель в какое-нибудь место экрана там, где вы хотите,
чтобы был центр многоугольника. Нажмите левую кнопку и удерживая ее нажатой
перемещайте указатель. При этом за ним потянется многоугольник. Нажатие
клавиш , ?при
нажатой левой кнопке, позволяет увеличивать или уменьшать число сторон
многоугольника. Достигнув нужного положения и размера, отпустите кнопку.
Произойдет фиксирование правильного многоугольника с заданным числом сторон
и с центром в заданной точке.
Для изображения
правильных многоугольников в параллельной проекции в графическом редакторе
“Adobe Illustrator” можно воспользоваться
инструментами “Размер” и “Наклон”, окошечки которых расположены под окошечком
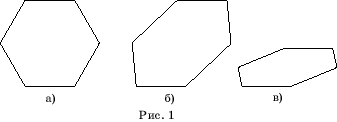
с изображением ножниц. Например, для построения параллельной проекции правильного
шестиугольника возьмем правильный шестиугольник (рис. 1,а) и применим к
нему инструмент “Наклон”. Получим шестиугольник, изображенный на рисунке
1,б. Применим к нему инструмент “Размер”, сжимая его по вертикали. Получим
шестиугольник, изображенный на рисунке 1,в, который и будет искомой параллельной
проекцией исходного правильного шестиугольника.
 Аналогичным
образом строятся параллельные проекции других правильных многоугольников.
Аналогичным
образом строятся параллельные проекции других правильных многоугольников.
Используя
эти изображения, можно строить изображения многогранников.
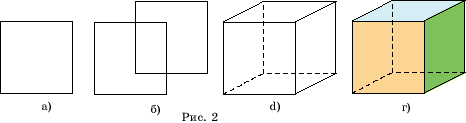
Например,
для построения изображения куба в параллельной проекции возьмем квадрат
(рис. 2,а). Это будет изображение передней грани куба. Скопируем ее и копию
параллельно перенесем на некоторый вектор (рис. 2,б). Это будет изображение
задней грани куба. Соединим отрезками соответствующие вершины передней
и задней граней и сделаем три невидимых ребра пунктирными. Получим искомое
изображение куба (рис. 2,в). Грани куба можно раскрасить в разные цвета
(рис. 2,г).
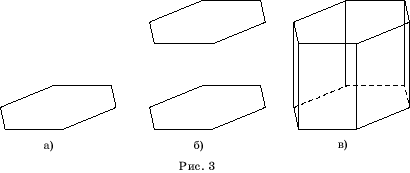
 Для построения
изображения правильной шестиугольной призмы воспользуемся изображением
правильного шестиугольника (рис. 3,а). Это будет изображение нижнего основания
призмы. Скопируем его и перенесем вертикально вверх на некоторое расстояние.
Это будет изображение верхнего основания призмы (рис. 3,б). Соединим отрезками
соответствующие вершины верхнего и нижнего оснований, и сделаем невидимые
ребра пунктирными. Получим искомое изображение правильной шестиугольной
призмы (рис. 3,в).
Для построения
изображения правильной шестиугольной призмы воспользуемся изображением
правильного шестиугольника (рис. 3,а). Это будет изображение нижнего основания
призмы. Скопируем его и перенесем вертикально вверх на некоторое расстояние.
Это будет изображение верхнего основания призмы (рис. 3,б). Соединим отрезками
соответствующие вершины верхнего и нижнего оснований, и сделаем невидимые
ребра пунктирными. Получим искомое изображение правильной шестиугольной
призмы (рис. 3,в).
 Так как параллельной
проекцией окружности является эллипс, то для получения изображения окружности
достаточно просто воспользоваться инструментом “Эллипс”.
Так как параллельной
проекцией окружности является эллипс, то для получения изображения окружности
достаточно просто воспользоваться инструментом “Эллипс”.
Для получения
изображения окружности с вписанным или описанным около нее правильным треугольником,
достаточно соответственно вписать или описать правильный треугольник около
исходной окружности (рис. 4,а), а затем сжать их в направлении одного из
диаметров (рис. 4,б).
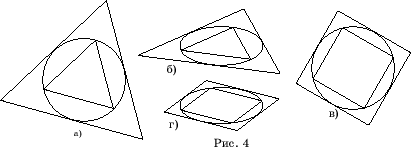 Аналогично,
для получения изображения окружности с вписанным или описанным около нее
квадратом, достаточно соответственно вписать или описать квадрат около
исходной окружности (рис. 4,в), а затем сжать их в направлении одного из
диаметров (рис. 4,г).
Аналогично,
для получения изображения окружности с вписанным или описанным около нее
квадратом, достаточно соответственно вписать или описать квадрат около
исходной окружности (рис. 4,в), а затем сжать их в направлении одного из
диаметров (рис. 4,г).
В некоторых
случаях изображения круглых тел требуется изобразить диаметр перпендикулярный
диаметру, изображение которого дано. Пусть, например, дано изображение
окружности и ее диаметра AB
(рис. 5,а). Требуется изобразить диаметр, ему перпендикулярный. Восстановим
окружность, сжатием которой получен эллипс и растянем изображение AB
диаметра в вертикальном направлении до
диаметра A’B’ этой окружности
(рис. 5,б). Повернем этот диаметр на 900.
Получим перпендикулярный диаметр C’D’.
Сожмем этот диаметр в вертикальном направлении до отрезка CD
с вершинами в точках эллипса (рис. 5,в). Этот отрезок CD и
будет искомым изображением.
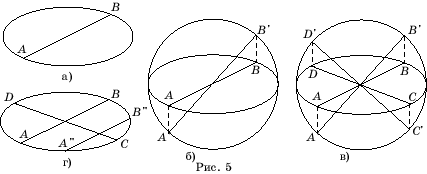 Изображение
перпендикулярного диаметра можно получить и по-другому. А именно, проведем
какую-нибудь хорду A”B”, параллельную
AB и через середины отрезков
AB и A”B”
проведем отрезок CD (рис. 5,г).
Он и будет искомым изображением.
Изображение
перпендикулярного диаметра можно получить и по-другому. А именно, проведем
какую-нибудь хорду A”B”, параллельную
AB и через середины отрезков
AB и A”B”
проведем отрезок CD (рис. 5,г).
Он и будет искомым изображением.
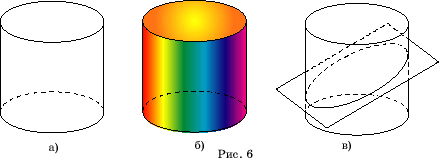
Используя
изображение эллипса, так же как и в случае призмы, можно получить изображение
цилиндра (рис. 6,а). Основание и боковую поверхность цилиндра можно раскрасить
(рис. 6,б).
На рисунке
6,в показано, как можно получить изображение сечения цилиндра плоскостью.
Для этого достаточно взять эллипс верхнего основания цилиндра, повернуть
его на некоторый угол, опустить вниз на некоторое расстояние и растянуть
так, чтобы он касался образующих цилиндра.
 Сфера обычно
изображается в ортогональной проекции. Изображение сферы с выделенным экватором
получается сжатием окружности в вертикальном направлении (рис. 7,а). Для
нахождения изображения полюсов будем считать исходное изображение сферы
видом спереди, и построим вид сферы слева. Большая окружность и ось сферы
изобразятся перпендикулярными диаметрами (рис. 7,б). Изображение полюсов
на основной плоскости получается параллельным переносом полюсов на виде
сферы слева.
Сфера обычно
изображается в ортогональной проекции. Изображение сферы с выделенным экватором
получается сжатием окружности в вертикальном направлении (рис. 7,а). Для
нахождения изображения полюсов будем считать исходное изображение сферы
видом спереди, и построим вид сферы слева. Большая окружность и ось сферы
изобразятся перпендикулярными диаметрами (рис. 7,б). Изображение полюсов
на основной плоскости получается параллельным переносом полюсов на виде
сферы слева.
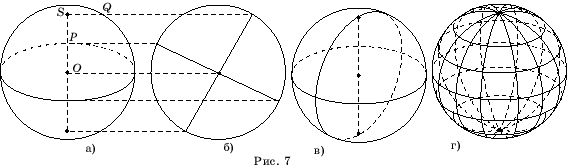 На практике
можно не прибегать к видe сферы слева. Для построения изображения полюсов
S1
и S2
достаточно заметить, что имеют место равенства отрезков OP =
SQ. После этого полюса сферы изображается
так, чтобы выполнялось это равенство (рис.
7,а). Для изображения меридиана (окружности, проходящей через полюса сферы)
достаточно сжать исходную окружность в эллипс, а затем повернуть его вокруг
центра так, чтобы он проходил через полюса (рис. 7,в). На рисунке 7,г показано
изображение нескольких меридианов и параллелей.
На практике
можно не прибегать к видe сферы слева. Для построения изображения полюсов
S1
и S2
достаточно заметить, что имеют место равенства отрезков OP =
SQ. После этого полюса сферы изображается
так, чтобы выполнялось это равенство (рис.
7,а). Для изображения меридиана (окружности, проходящей через полюса сферы)
достаточно сжать исходную окружность в эллипс, а затем повернуть его вокруг
центра так, чтобы он проходил через полюса (рис. 7,в). На рисунке 7,г показано
изображение нескольких меридианов и параллелей.
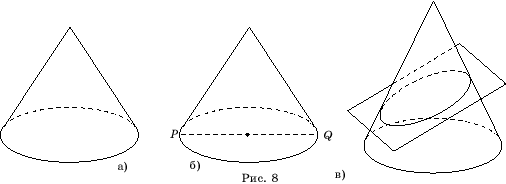
При изображении
конуса (рис. 8,а) следует иметь ввиду, что видимые образующие конуса касаются
эллипса, изображающего основание конуса, в точках, расположенных выше большой
оси этого эллипса (рис. 8,б). Изображение сечения конуса плоскостью (рис.
8,в) получается также как и изображение сечения цилиндра плоскостью.
 Рассмотрим
теперь вопрос об изображении вписанных и описанных многогранников.
Рассмотрим
теперь вопрос об изображении вписанных и описанных многогранников.
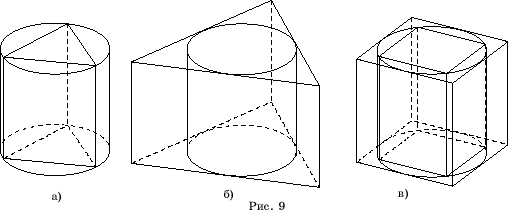
Для построения
изображения правильной треугольной призмы, вписанной в цилиндр воспользуемся
изображением правильного треугольника, вписанного в окружность. Это будет
изображение верхнего основания призмы. Скопируем его и перенесем вертикально
вниз на некоторое расстояние. Это будет изображение верхнего основания
призмы. Соединим отрезками соответствующие точки верхнего и нижнего оснований,
и сделаем невидимые ребра пунктирными. Получим искомое изображение правильной
треугольной призмы, вписанной в цилиндр (рис. 9,а). Аналогичным образом
строятся изображение правильной треугольной призмы описанной около цилиндра
(рис. 9,б) и правильных четырехугольных призм, вписанной и описанной около
цилиндра (рис. 9,в).
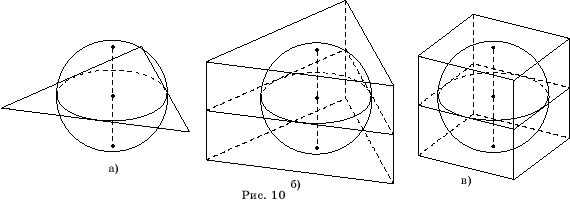
 Построим
правильную треугольную призму с вписанной в нее сферой. Для этого воспользуемся
изображением сферы и опишем около ее экватора правильный треугольник
(рис. 10,а). Скопируем этот треугольник и
перенесем его вертикально вверх и вниз на расстояние OS.
Это будут изображения верхнего и нижнего основания призмы. Соединим отрезками
соответствующие вершины верхнего и нижнего оснований, и сделаем невидимые
ребра пунктирными. Получим искомое изображение правильной треугольной призмы
с вписанной в нее сферой (рис. 10,б). Аналогичным образом строится изображение
куба с вписанной в него сферой (рис. 10,в).
Построим
правильную треугольную призму с вписанной в нее сферой. Для этого воспользуемся
изображением сферы и опишем около ее экватора правильный треугольник
(рис. 10,а). Скопируем этот треугольник и
перенесем его вертикально вверх и вниз на расстояние OS.
Это будут изображения верхнего и нижнего основания призмы. Соединим отрезками
соответствующие вершины верхнего и нижнего оснований, и сделаем невидимые
ребра пунктирными. Получим искомое изображение правильной треугольной призмы
с вписанной в нее сферой (рис. 10,б). Аналогичным образом строится изображение
куба с вписанной в него сферой (рис. 10,в).
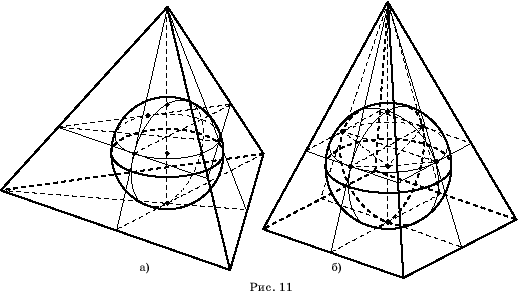
 На рисунках
11, а, б показаны изображения сферы, вписанной в тетраэдр и правильную
четырехугольную пирамиду.
На рисунках
11, а, б показаны изображения сферы, вписанной в тетраэдр и правильную
четырехугольную пирамиду.
Литература
1. Бескин Н.М. Изображение
пространственных фигур //Квант. – 1970. - № 12.
2. Бэйн С. Adobe
Illustrator 7. “BHV – Санкт-Петербург”, 1998.
3. Василевский А.Б. Метод
параллельных проекций. – Минск: Народная асвета, 1985.
4. Костицын В.Н. Моделирование
на уроках геометрии. – М.: Владос, 2000.
5. Польский И.Г. Проекционный
чертеж и построения на нем. – М.: Учпедгиз, 1962.
6. Смирнова И.М., Смирнов
В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.
7. Четверухин Н.Ф. Стереометрические
задачи на проекционном чертеже. – 3-е изд. – М.: Учпедгиз, 1955.
8. Четверухин Н.Ф. Чертежи
пространственных фигур в курсе геометрии. – М.: Учпедгиз, 1946.
9. Энциклопедия элементарной
геометрии. Книга IV. Геометрия. – М.: Гос. изд. физико-математ. лит., 1963,
с. 229.











