КРИВЫЕ, КАК ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК

    Кривые с древних времен привлекали к себе внимание ученых и использовались ими для описания различных природных явлений от траектории брошенного камня до орбит космических тел. В школьном курсе математики кривые рассматриваются как графики функций в курсе алгебры и начал анализа 10-11 классов. Конечно, это уже довольно поздно. Кроме того, при их изучении преобладает алгебраический аспект, связанный с выбранной системой координат. Геометрические же свойства остаются в стороне даже для таких известных кривых как парабола, эллипс, гипербола. Вместе с тем, определения этих и других кривых могут быть даны как геометрических мест точек без использования системы координат. Такой подход предоставляет широкие возможности для обобщающего повторения по теме “Геометрические места точек” в курсе геометрии 7-го класса и в том числе для повторения свойств биссектрисы, серединного перпендикуляра, касательной к окружности и т. д.

1. Парабола

    Пусть на плоскости задана прямая d и точка F, не принадлежащая этой прямой. Геометрическое место точек, равноудаленных от прямой d и точки F, называется параболой. Прямая d называется директрисой, а точка F - фокусом параболы (рис. 1).

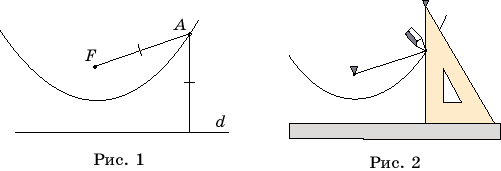
    Для того чтобы нарисовать параболу, потребуются линейка, угольник, нить длиной, равной большему катету угольника, и кнопки. Прикрепим один конец нити к фокусу, а другой - к вершине меньшего угла угольника. Приложим линейку к директрисе и поставим на нее угольник меньшим катетом. Карандашом натянем нить так, чтобы его острие касалось бумаги и прижималось к большему катету. Будем перемещать угольник и прижимать к его катету карандаш так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге параболу (рис. 2).
    Осью параболы называется прямая, проходящая через фокус и перпендикулярная директрисе. Точка пересечения параболы с ее осью называется вершиной параболы.
    Прямая, имеющая с параболой только одну общую точку и не перпендикулярная ее директрисе, называется касательной к параболе.
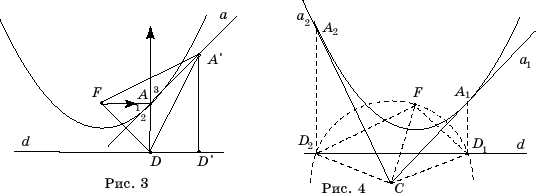
    Теорема. Пусть A – точка на параболе с фокусом F и директрисой d, АD – перпендикуляр, опущенный на директрису (рис. 3). Тогда касательной к параболе, проходящей через точку A, будет прямая, содержащая биссектрису угла FAD.
    Доказательство. Докажем, что прямая a, содержащая биссектрису угла FAD будет касательной к параболе (рис. 3). Действительно, треугольник FAD равнобедренный. Следовательно, прямая a будет серединным перпендикуляром к отрезку FD. Для произвольной точки A' прямой а, отличной от А, опустим перпендикуляр A'D' на прямую d. Тогда

А'F = A'D > A'D'.

Это означает, что точка A' не принадлежит параболе и, следовательно, прямая а имеет только одну общую точку А с параболой, т.е. является касательной.

    Фокальное свойство параболы. Если источник света поместить в фокус параболы, то лучи, отразившись от параболы, пойдут в одном направлении, перпендикулярном директрисе.
    Воспользуемся тем, что угол падения света равен углу отражения и тем, что от кривой свет отражается также как от касательной, проведенной в точку падения.
    Пусть A – точка падения луча, исходящего из фокуса F параболы, a – касательная, AD – прямая, перпендикулярная директрисе (рис. 3). Тогда углы 1 и 2 равны, так как касательная a содержит биссектрису угла FAD. Углы 2 и 3 равны, как вертикальные углы. Следовательно, углы 1 и 3 равны. Поскольку угол падения луча света в точке A равен углу 1, то угол отражения будет равен углу 3, т.е. направление отраженного луча будет перпендикулярно директрисе.
    Фокальное свойство параболы используется при изготовлении отражающих поверхностей прожекторов, автомобильных фар, карманных фонариков, телескопов, параболических антенн и т.д.
    Построение касательной к параболе. Пусть парабола задана фокусом F и директрисой d. Используя циркуль и линейку, построим касательную к параболе, проходящую через данную точку C.
    С центром в точке C и радиусом CF проведем окружность и найдем ее точки пересечения с директрисой d. Если расстояние от точки C до фокуса больше, чем расстояние до директрисы, то таких точек две (рис. 4). Обозначим их D₁ и D₂. Проведем биссектрисы углов FCD₁ и FCD₂ соответственно. Прямые a₁ и a₂, содержащие эти биссектрисы являются серединными перпендикулярами к отрезкам FD₁ и FD₂и, значит, будут искомыми касательными к параболе. Для построения точек касания через точки D₁ и D₂ проведем прямые, перпендикулярные директрисе и найдем их точки пересечения A₁ и A₂ с прямыми a₁ и a₂. Они и будут искомыми точками касания.
    Может случиться, что расстояние от точки C до фокуса равно расстоянию до директрисы. В этом случае точка C будет лежать на параболе, окружность с центром в точке C и радиусом CF будет касаться директрисы в некоторой точке D и, следовательно, через точку C будет проходить одна касательная – биссектриса угла FCD.
    В случае, если расстояние от точки C до фокуса меньше, чем расстояние до директрисы, то точек пересечения окружности с директрисой нет и, следовательно, нет касательных к параболе, проходящих через эту точку.
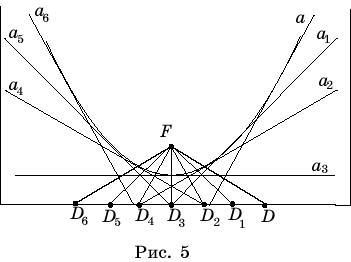
    Лабораторная работа. Укажем способ получения параболы из листа бумаги. Возьмем лист бумаги прямоугольной формы и отметим около его большой стороны точку F. Сложим лист так, чтобы точка F совместилась с какой-нибудь точкой D на большой стороне, и на бумаге образовалась линия сгиба a (рис. 5). Линия сгиба будет серединным перпендикуляром к отрезку FD и, следовательно, касательной к параболе. Разогнем лист и снова согнем его, совместив точку F с другой точкой большой стороны. Сделаем так несколько раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут касательными к параболе. Граница участка внутри этих сгибов будет иметь форму параболы (рис. 5).

2. Эллипс

    Геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек F₁, F₂ есть величина постоянная, называется эллипсом. Точки F₁, F₂ называются
фокусами эллипса.
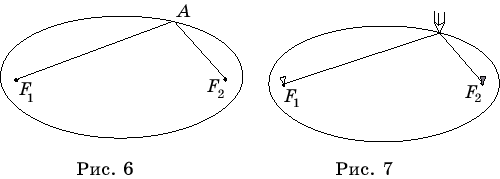
    Таким образом, для точек A эллипса с фокусами F₁ и F₂ сумма AF₁ + AF₂ постоянна и равна некоторому положительному числу c (рис. 6). Из неравенства треугольника следует, что c должно быть больше длины отрезка F₁F₂.

    Слово "фокус" в переводе с латинского языка означает "очаг", "огонь", и именно это свойство эллипса послужило основанием для названия точек F₁, F₂ фокусами.
    Еще И.Кеплер (1571-1630) обнаружил, что планеты Солнечной системы движутся вокруг Солнца не по окружностям, как думали раньше, а по эллипсам, причем Солнце находится в одном из фокусов этих эллипсов. Точка орбиты планеты, ближайшая к Солнцу, называется перигелий, а наиболее удаленная - афелий. Однако из-за того, что орбита Земли представляет собой очень мало сжатый эллипс, похожий на окружность, такое приближение и удаление от Солнца незначительно сказывается на температуре. Гораздо большее значение для температуры на поверхности Земли имеет угол падения солнечных лучей. Так, например, когда Земля находится в перигелии, в нашем полушарии зима, а когда в афелии – лето. Луна, искусственные спутники Земли также движутся вокруг Земли по эллипсам.
    Для того чтобы нарисовать эллипс, потребуется нить и кнопки. Прикрепим концы нити к фокусам. Карандашом натянем нить так, чтобы его острие касалось бумаги. Будем перемещать карандаш по бумаге так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге эллипс (рис. 7).
    Касательной к эллипсу называется прямая, имеющая с эллипсом только одну общую точку.
    Теорема. Пусть А - произвольная точка эллипса с фокусами F₁, F₂. Тогда касательной к эллипсу, проходящей через точку A, является прямая, содержащая биссектрису угла, смежного с углом F₁AF₂.
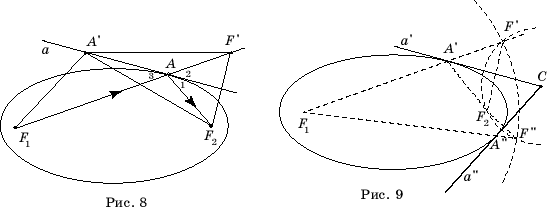
    Доказательство. Докажем, что прямая a, содержащая биссектрису угла, смежного с углом F₁AF₂, будет касательной к эллипсу (рис. 8). Обозначим AF₁ + AF₂ = c. Рассмотрим точку F' на прямой F₁A, для которой АF' = АF₂. Тогда прямая a будет серединным перпендикуляром к отрезку F₂F'. Для произвольной точки A’ прямой a, отличной от А, имеем

A’F₂ = A’F' и A’F₁ + A’F₂ = A’F₁ + A’F'> F₁F'= c.

Это означает, что точка A’ не принадлежит эллипсу, и, следовательно, прямая a имеет только одну общую точку А с эллипсом, т.е. является касательной.

    

    Фокальное свойство. Если источник света поместить в один из фокусов эллипса, то лучи, отразившись от эллипса, соберутся в другом его фокусе.
    Воспользуемся тем, что угол падения света равен углу отражения, и тем, что от кривой свет отражается также как от касательной, проведенной в точку падения.
    Пусть A – точка падения луча, исходящего из фокуса F₁ эллипса, a – касательная (рис. 8). Тогда углы 1 и 2 равны, так как касательная a содержит биссектрису угла F₂AF’. Углы 2 и 3 равны, как вертикальные углы. Следовательно, углы 1 и 3 равны. Поскольку угол падения луча света в точке A равен углу 3, то угол отражения будет равен углу 1, т.е. луч света после отражения в точке A пойдет в направлении AF₂.
    Построение касательной к эллипсу. Пусть эллипс задан своими фокусами и константой c. Используя циркуль и линейку, построим касательную к эллипсу, проходящую через данную точку C.
    С центром в точке C и радиусом CF₂ проведем окружность. С центром в точке F₁ и радиусом c проведем другую окружность и найдем ее точки пересечения с первой окружностью (рис. 9). Таких точек может быть – две F’, F” – одна или ни одной, в зависимости от расположения точки C. В первом случае проведем биссектрисы углов F’СF₂, F”СF₂. Соответствующие прямые a’, a” являются серединными перпендикулярами к отрезкам F’F₂,F”F₂и, значит, будут искомыми касательными к эллипсу. Для построения точек касания проведем прямые F₁F’, F₁F” и найдем их точки пересечения A’, A” с касательными a’, a” соответственно. Они и будут искомыми.
    Во втором случае, когда проведенные окружности имеют одну общую точку (касаются), будем иметь одну касательную. Если же окружности не имеют общих точек, то касательных нет.
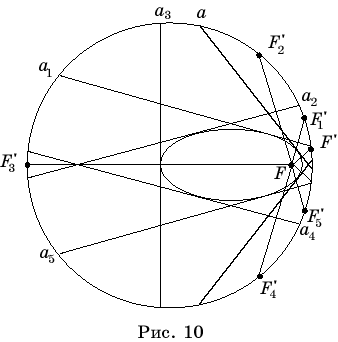
    Лабораторная работа. Укажем способ получения эллипса из листа бумаги. Вырежем из бумаги большой круг и в любом его месте, отличном от центра, поставим точку F. Сложим круг так, чтобы эта точка совместилась с какой-нибудь точкой F’ окружности круга, и на бумаге образовалась линия сгиба a (рис. 10). Линия сгиба будет серединным перпендикуляром к отрезку FF’ и, следовательно, касательной к эллипсу. Разогнем круг и снова согнем его, совместив точку с другой точкой окружности круга. Сделаем так несколько раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут касательными к эллипсу. Граница участка внутри этих сгибов будет иметь форму эллипса.
    Для другого способа получения эллипса потребуется сковорода и картонный круг диаметром вдвое меньше диаметра сковороды. Клейкой лентой укрепим на дне сковороды лист бумаги. Положив круг на сковороду, продырявим его в любом месте, отличном от центра, отточенным карандашом. Если теперь катить круг по краю сковороды, прижимая острие карандаша к бумаге, то на бумаге появится эллипс.

3. Гипербола

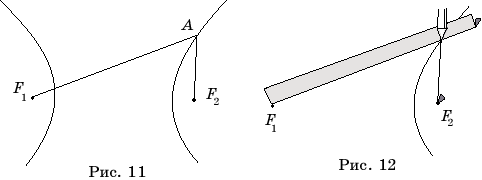
    Геометрическое место точек плоскости, модуль разности расстояний от которых до двух заданных точек F₁, F₂ есть величина постоянная, называется гиперболой. Точки F₁, F₂ называются фокусами гиперболы (рис. 11).

    Таким образом, для точек А гиперболы с фокусами F₁, F₂ выполняется равенство

|AF₁- AF₂| = c,

где c – некоторое фиксированное положительное число.
    Гипербола состоит из двух ветвей, для точек которых выполняется одно из равенств:

AF₁ - AF₂ = c, AF₂ – AF₁ = c.

    Из неравенства треугольника следует, что c должно быть меньше длины отрезка F₁F₂.
    Для того чтобы нарисовать гиперболу, потребуется линейка, нить, длина которой меньше длины линейки. Разность длин линейки и нити должна быть меньше, чем расстояние между фокусами. Прикрепим один конец нити к концу линейки, а второй конец к фокусу. Второй конец линейки совместим со вторым фокусом. Натянем нить, прижав ее к линейке острием карандаша (рис. 12). Если поворачивать линейку вокруг фокуса, прижимая к ней карандаш и оставляя нить натянутой, то карандаш будет описывать гиперболу.
    Рассмотрим ветвь гиперболы, точки которой удовлетворяют равенству AF₁ - AF₂ = c. Она разбивает плоскость на две области – внешнюю, для точек A’ которой выполняется неравенство A’F₁ – A’F₂ < c и внутреннюю, для точек A” которой выполняется неравенство A’F₁ – A’F₂ > c.
    Прямая, проходящая через точку А гиперболы, остальные точки A’ которой лежат во внешней области, т.е. удовлетворяют неравенству A’F₁ – A’F₂ < c, называется касательной к гиперболе. Точка А называется точкой касания.
    Аналогичным образом определяется касательная для точки, лежащей на другой ветви гиперболы.
    Теорема. Пусть А - точка гиперболы с фокусами F₁, F₂. Тогда касательной к гиперболе, проходящей через точку A, является прямая, содержащая биссектрису угла F₁AF₂.
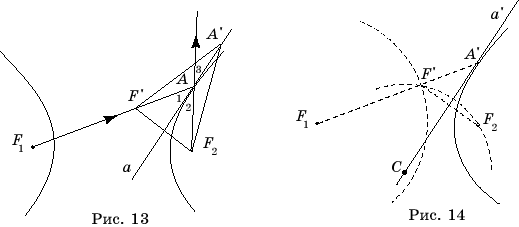
    Доказательство. Докажем, что прямая a, содержащая биссектрису угла F₁AF₂ будет касательной к гиперболе (рис. 13). Обозначим AF₁ - AF₂ = с. Рассмотрим точку F' на прямой F₁A, для которой АF' = АF₂. Тогда прямая a будет серединным перпендикуляром к отрезку F₂F'. Для произвольной точки A’ прямой a, отличной от А, имеем

A’F₂ = A’F' и A’F₁ – A’F₂ = A’F₁ – A’F' < F₁F' = c.

Следовательно, прямая a является касательной.

    Фокальное свойство гиперболы. Если источник света поместить в один из фокусов гиперболы, то лучи, отразившись от гиперболы, пойдут так, как будто бы они исходят из другого фокуса.
    Пусть A – точка падения луча, исходящего из фокуса F₁ гиперболы, a – касательная (рис. 13). Тогда углы 1 и 2 равны, так как касательная a содержит биссектрису угла F₁AF₂. Углы 2 и 3 равны, как вертикальные углы. Следовательно, углы 1 и 3 равны. Поскольку угол падения луча света в точке A равен углу 3, то угол отражения будет равен углу 1, т.е. луч света после отражения в точке A пойдет в направлении AF₂.
    Построение касательной к гиперболе. Пусть гипербола задана своими фокусами и константой c. Используя циркуль и линейку, построим касательную к гиперболе, проходящую через данную точку C.
    С центром в точке C и радиусом CF₂ проведем окружность. С центром в точке F₁ и радиусом c проведем другую окружность и найдем ее точки пересечения с первой окружностью (рис. 14). Таких точек может быть две F’, F”, одна или ни одной в зависимости от расположения точки C. В первом случае проведем биссектрисы углов F’СF₂, F”СF₂. Соответствующие прямые a’, a” являются серединными перпендикулярами к отрезкам F’F₂, F”F₂ и, значит, будут искомыми касательными к эллипсу. Для построения точек касания проведем прямые F₁F’, F₁F” и найдем их точки пересечения A’, A” с касательными a’, a” соответственно. Они и будут искомыми.
    Во втором случае, когда проведенные окружности имеют одну общую точку (касаются), будем иметь одну касательную. Если же окружности не имеют общих точек, то касательных нет.
    Лабораторная работа. Укажем способ получения гиперболы из листа бумаги. Вырежем из листа бумаги круг и отметим точку F на оставшейся части листа. Сложим лист так, чтобы эта точка совместилась с какой-нибудь точкой F’ окружности вырезанного круга, и на бумаге образовалась линия сгиба. Разогнем лист и снова согнем его, совместив точку с другой точкой окружности. Сделаем так несколько раз. Линии сгибов будут касательными к гиперболе. Граница участка внутри этих сгибов будет иметь форму гиперболы.

4. Именные кривые

    Рассмотрим еще несколько классических кривых, определяемых как геометрические места точек, носящих имена ученых, занимавшихся их изучением.
    Лемниската Бернулли представляет собой геометрическое место точек, произведение расстояний от которых до двух фиксированных точек F₁и F₂ равно a², где 2a – расстояние между F₁и F₂. Точки F₁, F₂ называются фокусами лемнискаты (рис. 15).

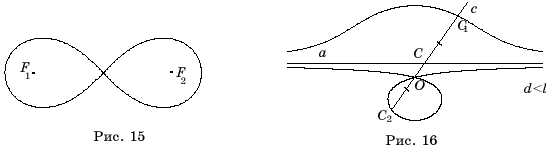
    Конхоида Никомеда – кривая, определяемая следующим образом. Через точку O, называемую полюсом конхоиды и отстоящую от прямой a, называемой ее базисом, на расстояние d, проведем прямую c, пересекающую прямую a в точке C. Отложим на прямой c по обе стороны от точки C на данном расстоянии l от нее точки C₁ и C₂, CC₁= CC₂= l. Проводя всевозможные прямые c, получим геометрическое место точек C₁ и C₂, образующих две ветви конхоиды. На рисунке 16 показан случай, когда d < l.
    Улитка Паскаля определяется так же как и конхоида, только в качестве базиса берется не прямая, а окружность. А именно, через точку O, называемую полюсом и расположенную на окружности радиуса R, называемой базисом, проведем прямую c, пересекающую окружность в точке C. Отложим на прямой c по обе стороны от точки C, на данном расстоянии l от нее, точки C₁ и C₂, CC₁= CC₂= l. Проводя всевозможные прямые c, получим геометрическое место точек C₁ и C₂, образующих улитку Паскаля. На рисунке 17 показан случай, когда 2R > l.

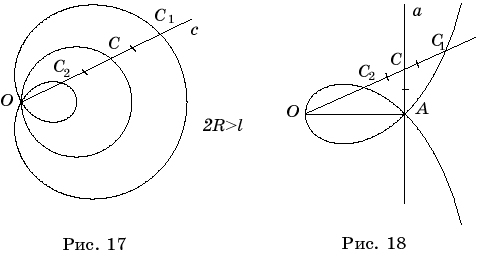
    Строфоида.Пусть дана прямая a и точка O, ей не принадлежащая. Опустим из точки O на прямую a перпендикуляр OA. Для точек C на прямой a рассмотрим лучи OC и будем откладывать на них отрезки CC₁ и CC₂ так, что CC₁=CC₂=CA. Геометрическое место таких точек C₁ и C₂ представляет собой кривую, называемую строфоидой (рис. 18). Точка O называется полюсом строфоиды.

   

Литература
1. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.
2. Бронштейн И. Эллипс. Гипербола. Парабола /Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. - / Приложение к журналу "Квант" № 2/2001.
3. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
4. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. - / Популярные лекции по математике, выпуск 4.
5. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.

6. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005.