ФРАКТАЛЫ

    Многие природные объекты и явления имеют не гладкий, а изломанный характер. Среди них листья деревьев, береговая линия, молния и др.
     Для описания этих объектов не подходят обычные дифференцируемые функции, с которыми имеет дело классический математический анализ.
     В последние десятилетия возникло и развивается новое направление в математике – фрактальная геометрия. Слово "фрактал" ввел в 1975 г. Б. Мандельброт (от латинского слова "fractus" - изломанный, дробный).
    Особенностью фракталов является не только их изломанность, но и самоподобность, означающая, что каждая часть фрактала подобна целому. Свойство самоподобности также отражает особенность природных объектов, когда отдельная клетка растения или животного несет в себе полную информацию обо всем организме.
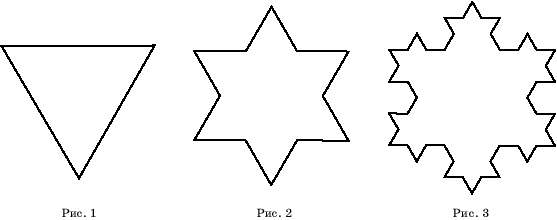
    Один из первых примеров фракталов был придуман еще в начале 20-го века немецким математиком Х. Кох (1870-1924) и называется звезда Коха. Для ее построения берется равносторонний треугольники последовательно добавляются к нему новые, подобные ему, треугольники. На первом шаге стороны правильного треугольника (рис. 1) разбиваются на три равные части и их середины заменяются на правильные треугольники, подобные исходному. В результате получается правильный звездчатый шестиугольник (рис. 2). Стороны этого шестиугольника снова разбиваются на три равные части, и их середины заменяются на правильные треугольники (рис. 3).

    Повторяя этот процесс, будем получать все более сложные многоугольники (рис. 4, 5), все более приближающиеся к предельному положению – звезде Коха.

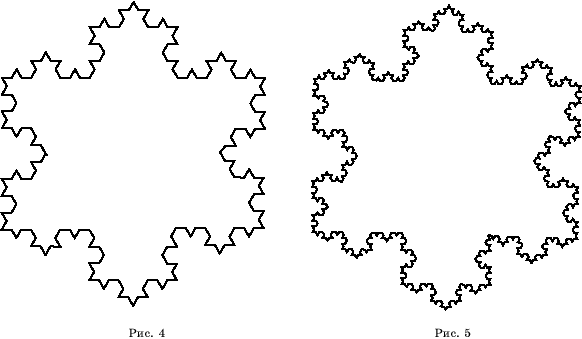
    Отметим, что кривая, ограничивающая звезду Коха непрерывна, но не дифференцируема ни в одной точке. Найдем ее длину. Предположим, что сторона исходного равностороннего треугольника равна единице и, следовательно, его периметр равен трем. На следующем шаге число сторон увеличивается в четыре раза и длина каждой из них в три раза меньше исходной. Поэтому периметр правильного звездчатого шестиугольника будет равен 3(4/3) = 4. Аналогично, на каждом следующем шаге периметр многоугольника увеличивается в 4/3 раза, становясь все больше и больше. Из этого следует, что кривая Коха, к которой приближаются многоугольники, будет иметь бесконечную длину.
    Вычислим площадь звезды Коха. Пусть площадь исходного равностороннего треугольника равна 1. На первом шаге мы добавляем три равносторонних треугольника, со сторонами в три раза меньшими исходных. Площадь каждого такого треугольника равна 1/9. Следовательно, площадь правильного звездчатого шестиугольника (рис. 2) равна 1+3/9=4/3. На следующем шаге добавляется двенадцать треугольников, суммарной площади 12/81. Поскольку длины сторон треугольников на каждом шаге уменьшаются в три раза, то их площадь уменьшается в девять раз. Число добавляемых треугольников равно числу сторон многоугольника и на каждом шаге увеличивается в четыре раза. Поэтому площадь S звезды Коха представляет собой площадь исходного треугольника плюс сумма геометрической прогрессии с начальным членом 3/9 и знаменателем 4/9. По формуле суммы геометрической прогрессии находим S=1+3/5=8/5.
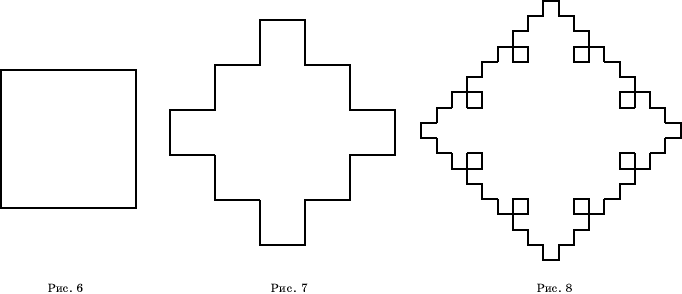
    Еще один вариант звезды Коха можно построить из квадратов, последовательным добавлением к исходному квадрату подобных ему квадратов.
    На первом шаге стороны квадрата (рис. 6) разбиваются на три равные части и их середины заменяются на квадраты, подобные исходному (рис. 7). Стороны получившегося многоугольника снова разбиваются на три равные части и их середины заменяются на квадраты (рис. 8).

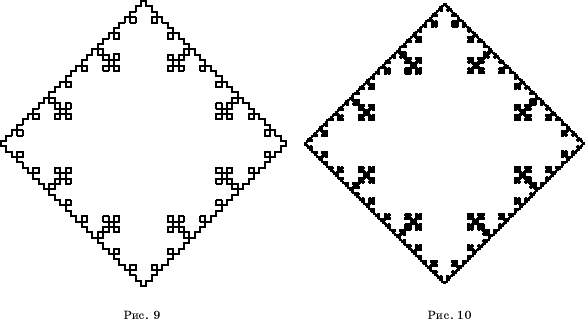
    Повторяя этот процесс, будем получать все более сложные многоугольники (рис. 9, 10), все более приближающиеся к искомой фигуре.

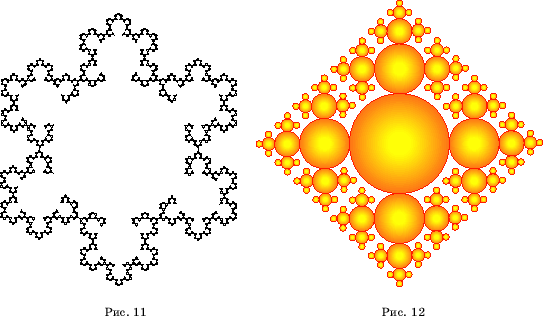
    На рисунках 11, 12 показаны фигуры Коха, построенные из шестиугольников и окружностей.

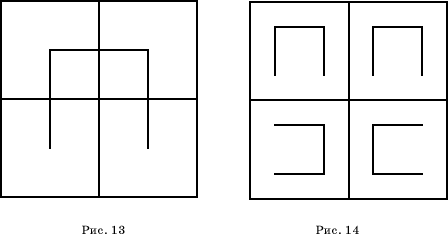
    Интересный пример кривой, имеющий фрактальный характер, был получен Д.Пеано (1858-1932) и называется кривой Пеано. Для ее построения разобьем данный квадрат на четыре равные квадрата и соединим их центры тремя отрезками, как показано на рисунке 13. Уберем внутренние стороны квадратов и из четырех их копий составим фигуру, изображенную на рисунке 14.

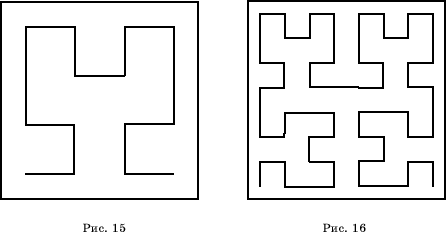
    Снова уберем внутренние стороны квадратов и соединим тремя отрезками концы ломаных, как показано на рисунках 15, 16.

    Повторяя описанную процедуру, будем получать все более сложные ломаные (рис. 17, 18), приближающиеся к кривой Пеано.

    Отметим, что кривая Пеано непрерывна. Ломаные, участвующие в построении кривой Пеано, на каждом этапе проходят через все квадраты, а сами квадраты уменьшаются, стягиваясь к точкам исходного квадрата. Поэтому кривая Пеано будет проходить через все точки исходного квадрата, т.е. она будет полностью заполнять весь исходный квадрат. Конечно, она будет иметь бесконечную длину.
    Рассмотрим еще один пример самоподобной фигуры, придуманный польским математиком В.Серпинским (1882-1969) и называемую ковром Серпинского.
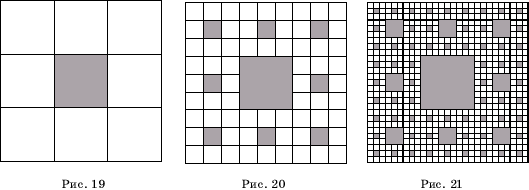
    Она получается из квадрата последовательным вырезанием серединных квадратов. А именно, разделим данный квадрат на девять равных квадратов и серединный квадрат вырежем. Получим квадрат с дыркой (рис. 19). Для оставшихся восьми квадратов повторим указанную процедуру. Разделим каждый из них на девять равных квадратов и серединные квадраты вырежем (рис. 20). Повторяя эту процедуру, будем получать все более дырявую фигуру (рис. 21). То, что остается после всех вырезаний, и будет искомым ковром Серпинского.

    Отметим, что поскольку вырезаемые квадраты располагаются все более часто, то в результате на ковре Серпиского не будет ни одного, даже самого маленького, квадрата без дырки.
    Вычислим площадь ковра Серпинского, считая исходный квадрат единичным. Для этого достаточно вычислить площадь вырезаемых квадратов. На первом шаге вырезается квадрат площади 1/9. На втором шаге вырезается восемь квадратов, каждый из которых имеет площадь 1/81. На каждом следующем шаге число вырезаемых квадратов увеличивается в восемь раз, а площадь каждого из них уменьшается в девять раз. Таким образом, общая площадь вырезаемых квадратов представляет собой сумму геометрической прогрессии с начальном членом 1/9 и знаменателем 8/9. По формуле суммы геометрической прогрессии находим, что это число равно единице, т.е. площадь ковра Серпинского равна нулю.
   Также как и раньше в этом ковре Серпиского не будет ни одного, даже самого маленького, квадрата без дырки. Однако, в отличие от обычного ковра Серпинского, его площадь будет отлична от нуля. Действительно, площадь вырезаемых квадратов представляет собой сумму геометрической прогрессии с начальным членом 1/2 и знаменателем 1/2, т.е. равна 1. Поэтому площадь оставшейся части будет равна единице.
    Начиная не с квадрата, а с правильного треугольника, и вырезая центральные треугольники, получим самоподобную фигуру, аналогичную ковру Серпинского и называемую салфеткой Серпинского (рис. 22).

    Интересным примером автоподобной кривой является “кривая дракона”, придуманная Э.Хейуэем. Для ее построения возьмем отрезок (рис. 23). Повернем его на 90 вокруг одной из вершин и добавим полученный отрезок к исходному. Получим угол из двух отрезков (рис. 24). Повторим описанную процедуру. Повернем угол на 90 вокруг вершины и добавим полученную ломаную к исходной (рис. 25).

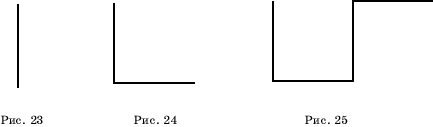
    Повторяя описанную процедуру и уменьшая ломаные, будем получать все более сложные ломаные, напоминающие дракона (рис. 26-34).

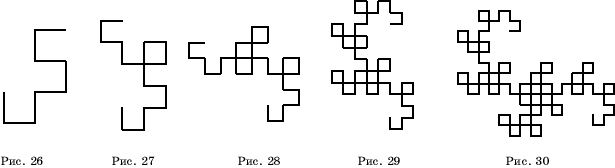
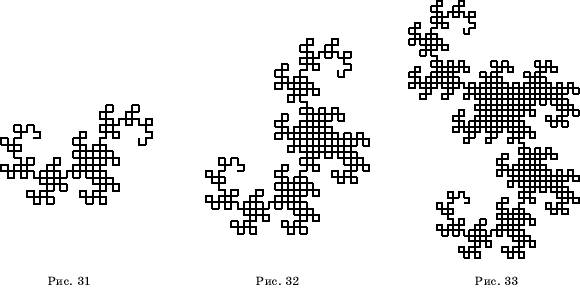
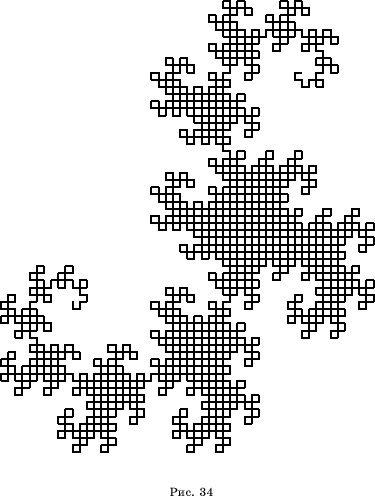
    Ниже приведено еще несколько примеры фракталов

           

         Интересным свойством фракталов является наличие у них дробной размерности. Напомним, что площадь S плоской фигуры Ф можно выразить формулой , где  - наименьшее число квадратов со стороной , покрывающих фигуру Ф.         Положительное число S_d  называется  d-мерой фигуры A, если . Число d называется фрактальной размерностью фигуры Ф.

         Выведем формулу для фрактальной размерности. Так как при  стремящемся к нулю число  стремится к S_d, то  будет стремиться к ln(S_d), то  будет стремиться к ln(S_d). Следовательно, . Так как , то окончательно получаем формулу .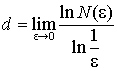

         Найдем фрактальную размерность ковра Серпинского, полученного из единичного квадрата. Если , то =8ⁿ. Следовательно, .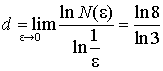

         Найдем фрактальную размерность звезды Коха, полученной из единичного правильного треугольника. Если , то =. Следовательно, .

Литература
1. Вишик М.И. Фрактальная размерность множеств. Соросовский образовательный журнал. № 1, 1998.
2. Жиков В.И. Фракталы. Соросовский образовательный журнал. № 12, 1996.
3. Морозов А.Д. Введение в теорию фракталов. – М. 2004.

4. Федер Е. Фракталы. Пер. с англ. - М.: Мир, 1991.