ЧИСЛА ФИБОНАЧЧИ

    Числа Фибоначчи появились в 1202 году в книге итальянского математика Леонардо из Пизы, более известный под именем Фибоначчи – сын Боначчи. В этой книге содержалась следующая задача о кроликах:
    Задача 1. Сколько пар кроликов рождается от одной новорожденной пары, если каждая пара кроликов каждый месяц, начиная со второго после своего рождения, производит на свет одну пару кроликов?
    Решение. В первый месяц новых пар еще не родится, и будет одна пара кроликов. Во второй месяц появится одна пара кроликов. Вместе с исходной они составят две пары. В третий месяц первая пара даст одну пару кроликов, а родившаяся во втором месяце еще нет. Таким образом, в третьем месяце будет три пары, из которых в следующем месяце две смогут дать потомство. В четвертом месяце родится две пары, и всего будет пять пар кроликов, из которых в следующем месяце три пары смогут дать потомство. В пятом месяце родится три пары, и всего будет 8 пар кроликов, из которых в следующем месяце 5 смогут дать потомство. Пусть количество пар кроликов в n-ом месяце равно u_n, а в n-1-ом месяце – u_n-1. Тогда количество пар кроликов в n+1-ом месяце будет выражаться рекурентной формулой u_n+1 = u_n + u_n-1.
    Числа, выписанные в последовательность, первые два числа в которой равны 1, и каждое следующее число равно сумме двух предшествующих, называются числами Фибоначчи. Вот несколько первых из них: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
    Рассмотрим еще две задачи, в которых появляются числа Фибоначчи.
    Задача 2. Сколькими способами может подняться человек по ступенькам лестницы на 10-ю ступеньку, если с каждой ступеньки он может шагать или на следующую, или через одну ступеньку?
    Решение. На первую ступеньку человек может попасть только одним способом. На вторую ступеньку можно подняться двумя способами, или двумя шагами, или одним. Ясно, что на n+1-ю ступеньку человек может попасть или с n-ой, или с n-1-ой ступеньки. Если число различных путей до n-ой ступеньки обозначить s_n, то s_n+1 = s_n + s_n-1, т.е. число различных путей выражается числами Фибоначчи. Следовательно, искомое число способов, которыми человек может подняться на 10-ю ступеньку, равно 55.

    Задача 3. Сколькими способами можно пройти по ориентированному графу из вершины A в вершину B?

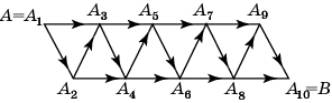
Так как в каждую вершину графа, начиная с третьей, можно попасть из вершин с номерами меньшими на 1 и 2, то искомое число способов выражается числами Фибоначчи и, следовательно равно 55.

Рассмотрим некоторые свойства чисел Фибоначчи.

    Свойство 1. u₁ + u₂ + … + u_n = u_{n +2} – 1.

Доказательство. Имеем

u₁ = u₃ – u₂,
u₂ = u₄ – u₃,
u₃ = u₅ – u₄,
…
u_n-1 = u_n+1 – u_n,
u_n = u_n+2 – u_n+1.

Сложим эти равенства почленно. Получим

u₁ + u₂ + … + u_n = u_{n +2} – 1.

    Свойство 2. u₁ + u₃ + … + u_2n-1 = u_2n.
    Доказательство. Имеем

u₁ = u₂,
u₃ = u₄ – u₂,

u₅ = u₆ – u₄,

…

u_2n-1 = u_2n – u_2n-2.

Складывая почленно, получим требуемое равенство.

Аналогичным образом доказывается, что имеет место равенство u₂ + u₄ + … + u_2n = u_2n+1 – 1.

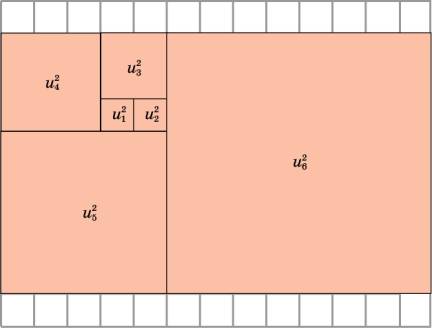
Свойство 3. u₁² + u₂² + … + u_n² = u_nu_n+1.

Доказательство. Заметим, что u_ku_k+1 – u_k-1u_k = u_k(u_k+1 – u_k-1) = u_k². Тогда

u₁² = u₁u₂,

u₂² = u₂u₃ – u₁u₂,

…

u_n² = u_nu_n+1 – u_n-1u_n.

Складывая эти равенства почленно, получим требуемое равенство.

Данное равенство можно получить, используя геометрические соображения. Так, например, на рисунке квадраты со сторонами u₁, u₂, …, u₆, составляют прямоугольник со сторонами u­₆, u_7.

 

    Свойство 4. u_n+m = u_n-1u_m + u_nu_m+1.
    Доказательство. Человек, шагающий по ступенькам, может попасть на n+m-ю ступеньку или перепрыгнув через n-ю, или наступив на нее. В первом случае он доходит до n-1-ой ступеньки u_n-1 способами, а затем с n+1-ой ступеньки до n+m-ой u_m способами. Во втором случае он доходит до n-ой ступеньки u_n способами, а затем с n-ой ступеньки до n+m-ой u_m+1 способами. Всего получается u_n-1u_m + u_nu_m+1 способов.

Свойство 5. Если n делится на m, то u_n делится на u_m.
    Докажите самостоятельно.

Свойство 6. Соседние числа Фибоначчи взаимно просты.
    Докажите самостоятельно.

Числа Фибоначчи тесно связаны с золотым отношением.

Теорема. Отношение предыдущего числа Фибоначчи к последующему при увеличении номеров стремится к золотому отношению j.

Действительно, из равенства a_n+1 = a_n + a_n-1 следует равенство 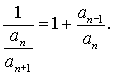 Поэтому отношение предыдущего числа к последующему будет стремиться к числу, удовлетворяющему уравнению , т.е. к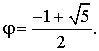   

Числа Фибоначчи связаны и с биномиальными коэффициентами. А именно, рассмотрим треугольник Паскаля, записанный в виде

1  
1 1
1 2 1
1 3 3 1
1 4 6 4 1
…………

Тогда суммы чисел, стоящих на диагоналях, расположенных под углом 45^о к многоточию, являются числами Фибоначчи. Докажите это самостоятельно.

Найдем формулу для n-го числа Фибоначчи. Для этого рассмотрим множество последовательностей, удовлетворяющих уравнению

u_n+1 = u_n + u_n-1 (*)

Теорема. Множество решений уравнения (*) является линейным пространством размерности 2.

Действительно, если (a_n) и (b_n) – последовательности, удовлетворяющие уравнению (*), то непосредственная проверка показывает, что для любых чисел s и t последовательность (sa_n + tb_n) будет решением уравнения (*). Поскольку каждая последовательность, удовлетворяющая уравнению (*), однозначно определяется двумя первыми своими членами, то линейное пространство решений уравнения (*) будет двумерно (изоморфно R²).

Следствие. Если (a_n) и (b_n) – два линейно независимых решения уравнения (*), то любое его решение представимо в виде u_n = sa_n + tb_n.

Выясним, какие геометрические прогрессии являются решениями уравнения (*).

Возьмем прогрессию 1, q, q², … . Для того, чтобы она была решением уравнения (*) необходимо и достаточно, чтобы выполнялось равенство qⁿ = q^n-1 + q^n-2, или q² = q +1. Решая последнее уравнение, находим два корня 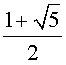 и 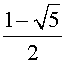. Геометрические прогрессии с начальным членами 1 и этими знаменателями будут линейно независимыми решениями уравнения (*).

Найдем такие числа s и t для которых первые два члена геометрической прогрессии равны первым двум числам Фибоначчи, т.е.

s + t = 1,

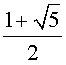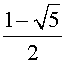s +t = 1.

Решая систему уравнений, находим 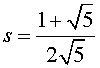, 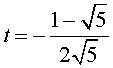. Следовательно, n-ое число Фибоначчи u_n выражается формулой

u_n = – = .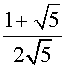

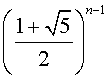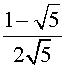
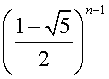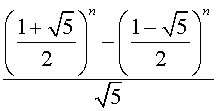Она называется формулой Бине (по имени математика, который ее вывел).

         Задача. Выведите явную формулу для n-го члена последовательности (a_n), задаваемую рекурентной формулой a_n+1 = 2a_n + a_n-1, и начальными условиями: a₁ = 1, a₂ = 1.

         Ответ.

Литература

1. Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969.

2. Виленкин Н.Я. и др. За старницами учебника математики, 10-11. – М.: Просвещение, 1996.

3. Волошинов А.В. Математика и искусство. – М.: Просвещение, 1992.

4. Воробьев Н.Н. Числа Фибоначчи. – 6-ое изд., доп. – М.: Наука, 1992.

5. Жуков А., Савин А. Числа Фидия и золотое сечение // Энциклопедия для детей. – т. 11. – М.: Аванта, 1998.

6. Замечательные числа. Числа Фибоначчи //Квант, 1988, № 3, с. 33.

7. Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1966.

8. Кордемский Б.А. Математическая смекалка. – М.:Наука, 1974, с. 365.

9. Маркушевич А.И. Возвратные последовательности. – М.: Наука, 1979.

10. Пойа Д. Математическое открытие. – М.: Наука, 1976.

11. Реньи А. Трилогия о математике. - М.: Мир, 1980, с. 326.

12. Спивак А. Числа Фибоначчи // Квант. – 2003. - № 2. – с. 32, 33.

13. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики (арифметика и алгебра). – М.: Наука, 1976.

14. Энциклопедический словарь юного математика. М.: Педагогика, 1989.

15. Яглом И.М. Итальянский купец Леонардо Фибоначчи и его кролики // Квант. – 1984, № 7, с. 15-17.

16. Васютинский Н.А. Золотая пропорция. М.: ДИЛЯ, 2006.