АНАЛИТИЧЕСКОЕ ЗАДАНИЕ МНОГОГРАННИКОВ.
ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
    Как известно из курса геометрии, плоскость в пространстве задается уравнением ax + by + cz + d = 0. При этом неравенства ax + by + cz + d  0 и ax + by + cz + d  0 определяют полупространства, на которые эта плоскость разбивает пространство. Для того, чтобы определить, какому из двух полупространств принадлежит точка A(x, y, z), достаточно подставить ее координаты в левую часть уравнения плоскости и найти знак получившегося значения.
    Поменяв знаки у чисел a, b, c, d, второе неравенство всегда можно свести к первому.
    Покажем, как с помощью таких неравенств в пространстве можно задавать выпуклые многогранники.
    Действительно, пусть грани выпуклого многогранника лежат в плоскостях, задаваемых уравнениями
a1x + b1y + c1z + d1 = 0,

........................,

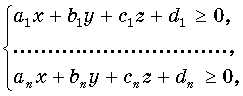
anx + bny + cnz + dn = 0.

Тогда сам многогранник является пересечением соответствующих полупространств и, следовательно, для его точек должна выполняться система неравенств
которая и определяет этот многогранник.
    Например, неравенства
x 0, y 0, z  0, x1, y1, z  1,
которые можно переписать в виде системы
определяют единичный куб в пространстве (рис. 1).
    Если к этим неравенствам добавить еще одно неравенство
x + y + z 2,
то соответствующий многогранник получается из куба отсечением пирамиды (рис. 2).
    Легко видеть, что неравенство |x|+|y|+|z|  a задает в пространстве октаэдр.

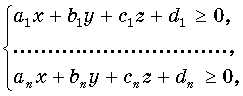
    Упражнения.
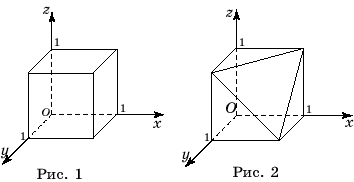
    1. Изобразите многогранник, состоящий из точек, координаты которых удовлетворяют неравенствам |x+y|+|z| 1, |x-y|-|z| 1или неравенствам |x-y|+|z|  1, |x+y|-|z|  1.
    2. Докажите, что точки с координатами (0, ±j, ± 1), (± 1, 0, ±j ), (±j , ±1, 0), где j= 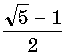, являются вершинами икосаэдра.
    3. Докажите, что точки с координатами (0, ±F, ±j ), (±j , 0, ±F ), (±F , ±j , 0), (± 1, ± 1, ±1), где j= 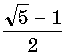, F = 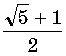, являются вершинами додекаэдра.
    4. При каком значении a неравенства

a|x| + |y|  3, a|y| + |z|  3, a|z| + |x| 3
задают додекаэдр?
    5. При каком значении a неравенства
(1-a)|x| + |y|  3, (1-a)|y| + |z|  3, (1-a)|z| + |x|  3, |x|+|y|+|z|  3(1+a)
задают икосаэдр?

    Ярким примером применения многогранников является ее использование в теории оптимального управления.
    Выпуклые многогранники можно трактовать аналитически – с помощью системы линейных неравенств. Линейная функция, рассматриваемая на таком выпуклом многограннике, достигает своего наибольшего (наименьшего) значения в одной из его вершин, либо на некотором ребре, либо на некоторой грани. В любом случае существует вершина (хотя бы одна), в которой принимается это наибольшее (наименьшее) значение. Найти это наибольшее (наименьшее) значение можно алгебраически, найдя значения линейной функции во всех вершинах многогранника и выбрав из них наибольшее (наименьшее).
    Оказалось, что к данной задаче отыскания наибольшего (наименьшего) значения линейной функции на многограннике приводят многие практические задачи. Среди них:
    транспортная задача о составлении оптимального способа перевозок грузов;
    задача о диете, т.е. о составлении наиболее экономного рациона питания, удовлетворяющего определенным медицинским требованиям;
    задача составления оптимального плана производства;
    задача рационального использования посевных площадей и т.д.
    Несмотря на различные содержательные ситуации в этих задачах, математические модели, их описывающие, имеют много общего, и все они решаются одним и тем же методом, разработанным отечественным математиком Л.В. Канторовичем (1912-1986).
    В своей книге "Математические методы организации и планирования производства" он заложил основы того, что ныне называется математической экономикой. Методы, развитые Канторовичем положили начало новому направлению прикладной математики – линейному программированию, изучающему численные методы решения задач отыскания наибольших и наименьших значений линейных функций на выпуклых многогранниках.
    За разработку этого направления в 1975 году Л.В. Канторович был удостоен Нобелевской премии.
    В качестве примера рассмотрим упрощенный вариант транспортной задачи.
    Задача. Пусть на четыре завода З1, З2, З3, З4 требуется завезти сырье одинакового вида, которое хранится на двух складах С1, С2. Потребность данных заводов в сырье каждого вида указана в таблице 1, а расстояние от склада до завода - в таблице 2. Требуется найти наиболее выгодный вариант перевозок, т. е. такой, при котором общее число тонно-километров наименьшее.

    Таблица 1
Наличие сырья, (в т) на складе Потребность в сырье, (в т) на заводе
С1 С2 З1 З2 З3 З4
20  25 8  10 12 15

    Таблица 2
Склад Расстояние (в км) от склада до завода 
З1 З2 З3 З4
C1 5 6 4 10
С2 3 7 3  7

    Для решения этой задачи, в первую очередь, проанализируем ее условие и переведем его на язык математики, т. е. составим математическую модель. Для этого количество сырья, которое нужно перевезти со склада С1 на заводы З1, З2, З3, обозначим через x, y и z соответственно. Тогда на четвертый завод с этого склада нужно будет перевезти 20 - x – y - z сырья в тоннах, а со второго склада нужно будет перевезти соответственно 8 - x, 10 - y, 12 - z, x + y + z - 5 сырья в тоннах. Запишем эти данные в таблицу 3.

    Таблица 3

Склад Кол-во сырья (в т), перевезенное на заводы
З1 З2 З3 З4
С1 x  y z 20–x–y - z
С2 8 – x 10 - y 12 - z x + y + z - 5

    Поскольку все величины, входящие в эту таблицу, должны быть неотрицательными, получим следующую систему неравенств

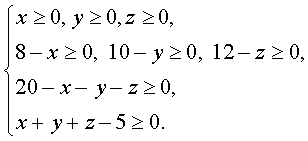
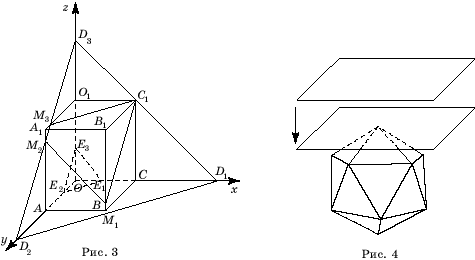
    Эта система неравенств определяет некоторый многогранник. Для того чтобы его построить, изобразим сначала многогранник, определяемый первой и второй строкой данной системы. На рисунке 3 это параллелепипед OABCO1A1B1C1. Уравнение 20 - x - y - z = 0 определяет плоскость D1D2D3, которая, пересекая параллелепипед, образует многоугольник M1M2M3C1. Уравнение
x + y + z - 5 = 0 определяет плоскость, которая пересекает параллелепипед и образует в нем треугольник E1E2E3. На многограннике M1M2M3C1CBAE1E2E3O1, где M1(8,10,2), M2(0,10,10), M3(0,8,12), C1(8,0,12), C(8,0,0), B(8,10,0), A(0,10,0), E1(5,0,0), E2(0,5,0), E3(0,0,5), O1(0,0,12), выполняются все условия данной системы. Назовем его многогранником ограничений.
    Для нахождения общего числа тонно-километров умножим расстояния от складов до заводов на перевозимое количество сырья и полученные результаты сложим. Общее число тонно-километров выражается формулой:

5x + 6y + 4z + 10(20 - x - y - z) + 3(8 - x) + 7(10 - y) +
+ 3(12 - z) + 7(x + y + z - 5) = 295 - x - 4y - 2z.
    Таким образом, задача сводится к отысканию наименьшего значения функции F=295-x-4y-2z на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f = x + 4y + 2z. Тогда Fmin = 295 - fmax.
    Используя геометрические соображения, докажем, что линейная функция вида ax+ by + cz  (c > 0) принимает свое наибольшее значение на многограннике в одной из его вершин.
    Зафиксируем какое-нибудь значение d функции ax + by + cz. Тогда уравнение ax + by + cz = d задает плоскость в пространстве, которая характеризуется тем, что во всех ее точках данная линейная функция принимает значение d. В точках, расположенных выше этой плоскости, она принимает значения, большие d, а в точках, расположенных ниже этой плоскости - значения, меньшие d. Если число d выбрать достаточно большим, то плоскость ax + by + cz = dрасположится выше многогранника. Будем опускать эту плоскость, уменьшая значения d, до тех пор, пока она не соприкоснется с многогранником. Такое касание произойдет при некотором d0 - в какой-нибудь вершине многогранника (рис. 4), или по какому-нибудь его ребру, или по какой-нибудь его грани.
    В точках касания линейная функция принимает значение d0, и, поскольку все остальные точки многогранника лежат ниже плоскости, значения линейной функции в этих точках меньше d0. Таким образом, d0 - искомое наибольшее значение. Поэтому для нахождения наибольшего значения линейной функции на многограннике, достаточно вычислить значения функции в вершинах многогранника и выбрать из них наибольшее. Вычислим значение функции f = x + 4y + 2z в вершинах многогранника ограничений: f(M1) = 52, f(M2) = 60, f(M3) = 56, f(C1) = 32, f(C) = 8, f(B) = 48, f(A) = 40, f(E1) = 5, f(E2) = 20, f(E3) = 10, f(O1) = 24.
    Легко видеть, что максимальное значение функции f равно 60. Тогда Fmin = 295 - 60 = 235. Это значение функция F принимает в точке M2(0,10,10).
    Таким образом, наиболее выгодный вариант перевозок задается таблицей 4.
    Таблица 4
Склад Кол-во сырья (в т), перевезенное на заводы
З1 З2 З3 З4
С1 0 10 10 0
С2 8 0 2 15
    Заметим, что число независимых переменных в этой задаче было равно трем и поэтому в процессе ее решения получился многогранник. Если бы число независимых переменных равнялось двум, то получился бы многоугольник. В реальных задачах число независимых переменных значительно больше трех, и для получения геометрической интерпретации этих задач требуется рассмотрение n-мерного пространства и n-мерных многогранников с очень большим n. При решении таких задач используются компьютеры.
    Таким образом, хотя пространственные свойства окружающего нас мира хорошо описываются геометрическим трехмерным пространством, потребности практической деятельности человека приводят к необходимости рассмотрения пространств большей размерности, которые изучаются в специальном разделе математики - многомерной геометрии.

    Литература
1. Беляева Э.С., Монахов В.М. Экстремальные задачи. – М.: Просвещение, 1977.
2. Болтянский В.Г. Математические методы оптимального управления. – М.: Наука, 1969.
3. Болтянский В.Г. Элементарная геометрия. – М.: Просвещение, 1985.
4. Волков В.А. Элементы линейного программирования. – М.: Просвещение, 1975.
5. Смирнова И.М. В мире многогранников. - М.: Просвеще-ние, 1995.
6. Тихомиров В.М. Рассказы о максимумам и минимумах. – М.: Наука, 1986.
7. Тихомиров В.М. 50 лет линейному программированию. – Квант, 1989, № 6, с. 9.
8. Тихонов А.Н., Костомаров Д.П. Рассказы о прикладной математике. – М.: Наука, 1979.
 
 

Hosted by uCoz