АНАЛИТИЧЕСКОЕ ЗАДАНИЕ КРИВЫХ НА ПЛОСКОСТИ

Существует несколько способов аналитического задания кривых на плоскости.

I. Задание кривой уравнением в декартовых координатах.

В качестве примера найдем уравнения задающие параболу, эллипс и гиперболу.

Парабола. Напомним, что параболой  называется  геометрическое  место точек, равноудаленных от данной прямой d и данной точки F. Прямая d называет­ся директрисой, а точка F - фокусом параболы.

Выведем уравнение, задающее параболу на координатной плоскости. Обозначим точку пересечения оси параболы с ее директрисой через G. Длину отрезка FG обозначим через 2а (рис. 1).

 

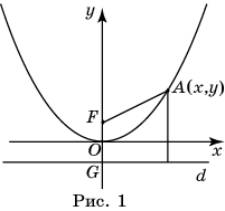
Введем систему коорди­нат, считая началом координат О середину отрезка FG, осью абсцисс – прямую, параллельную директрисе и проходящую через начало координат, осью ординат - ось параболы. Тогда фокус F будет иметь координаты (0, а).

Пусть А(x, y) - точка плоскости. Расстояния от нее до фокуса и директрисы равны соответственно  и |y+a|. Точка A принадлежит параболе в том и только том случае, когда выполняется равенство

 = y+a.

Возведя обе части этого равенства в квадрат и приведя подобные члены, будем иметь равенство

4ay = x²,

которое и будет искомым уравнением параболы.

Эллипс. Напомним, что эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек F₁, F₂ есть величина постоянная. Точки F₁, F₂ называются фокусами эллипса.

Выведем уравнение эллипса на координатной плоскости. Пусть F₁, F₂ - фокусы эллипса. Длину отрезка F₁F₂ обозначим через 2с. Введем систему координат, считая началом координат О середину отрезка F₁F₂, осью абсцисс - прямую F₁F₂, осью ординат - прямую, проходящую через начало координат и перпендикулярную оси абсцисс (рис. 2). Фокусы эл­липса будут иметь координаты F₁(-c, 0), F₂(c, 0).

 

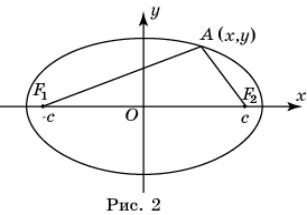
Пусть А(x, y) - точка плоскости. Расстояния от нее до фокусов равны соответственно  и . Точка A принадлежит эллипсу в том и только том случае, когда выполняется равенство

 +  = 2a,

где a – некоторое фиксированное число (a > 2c).

Перенесем второе слагаемое левой части этого равенства в правую часть и возведем обе части полученного равенства в квадрат. Будем иметь

Приведем подобные члены

=

Еще раз возведем в квадрат и приведем подобные члены

Обозначим  и разделим обе части равенства на  Получим равенство

(1)

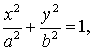
которое и будет искомым уравнением эллипса.

Гипербола. Напомним, что гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух заданных точек F₁, F₂ есть фиксированное число, взятое со знаком "+" или "–". Точки F₁, F₂ называются фокусами гиперболы.

Выведем уравнение гиперболы. Введем систему координат, считая осью Ox прямую, проходящую через фокусы, а осью Oy прямую, перпендику­лярную оси Ox , и делящую отрезок F₁F₂ пополам. Пусть фокусы имеют ко­ординаты F₁(-с, 0), F₂(с, 0) (рис.3).

 

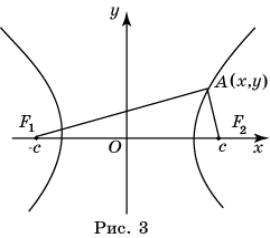
Точка А(x, y) принадлежит гиперболе тогда и только тогда, когда выполняется равенство AF₁ - AF₂ = 2a, где a – некоторое фиксированное число, 0 < a < c.

Перепишем это равенство в координатной форме

 -   = 2а.

Перенесем второй корень в правую часть и возведем обе части равенства в квадрат. Получим

Раскрывая скобки и приводя подобные члены, будем иметь равенство

Еще раз возводя в квадрат и обозначая , получим

.

Разделив обе части на , окончательно получим уравнение гиперболы

(2)

         II. Задание кривой уравнением в полярных координатах.

Наряду с декартовыми координатами на плоскости, во многих случаях более удобными оказываются так называемые полярные координаты.

При указании места расположения какого-нибудь объекта удобнее оп­ределять не его декартовы координаты, а направление и расстояние до объекта. Именно так в повседневной жизни показывают дорогу в городе. Например: "Вы пройдете по этой улице около 100 м, свернете направо, пройдете еще 50 м и будете у цели". При астрономических наблюдениях также гораздо удобнее использование не декартовых, а полярных коорди­нат.

Дадим определение полярных координат на плоскости. Пусть на плос­кости задана координатная прямая с выделенной точкой О и единичным от­резком ОЕ. Эта прямая в данном случае будет называться полярной осью. Точка O называется полюсом.

Полярными координатами точки А на плоскости с заданной полярной осью называется пара (r, φ), где r - расстояние от точки А до точки О, φ - угол между полярной осью и вектором , отсчитываемый в направлении против часовой стрелки, если φ > 0, и по часовой стрелке, если φ < 0 (рис. 4,а).

 

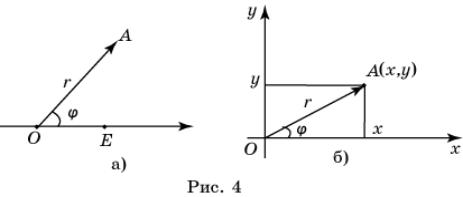
При этом первая координата r назы­вается полярным радиусом, а вторая φ - полярным углом. Полярный угол φ можно задавать в градусах или радианах.

Если на плоскости задана декартова система координат, то обычно за полюс принимается начало координат и за полярную ось – ось Ox. В этом случае каждой точке плос­кости с декартовыми координатами (x, y) можно сопоставить полярные ко­ординаты (r, φ) (рис. 4,б). При этом декартовы координаты выражаются через полярные по формулам

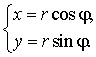
Наоборот, полярные координаты выражаются через декартовы по формулам

, ,  .

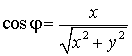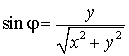Полярные координаты оказываются удобными для задания  кривых  на плоскости. Рассмотрим некото­рые из таких кривых.

Окружность радиуса R и центром в точке О задается уравнением r = R.

Действительно, окружность является геометрическим местом точек, удаленных от точки О на расстояние R. Все такие точки удовлетворяют равенству r = R. При этом, если угол φ увеличивается, соответствую­щая точка на окружности движется в направлении против часовой стрелки, описывая круги. Если же угол φ уменьшается, соответствующая точка описывает круги в направлении по часовой стрелке.

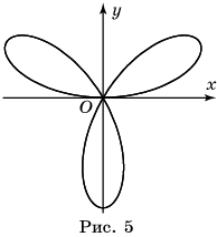
Трилистник – кривая, задаваемая уравнением r = sin 3 φ.

Для построения этой кривой сначала заметим, что, поскольку радиус неотрицателен, должно выполняться неравенство sin 3  0, решая которое находим область допустимых значений углов :

0    60; 120    180; 240   300.

Итак, пусть 0   60. Если угол  изменяется от нуля до 30, то sin 3 изменяется от нуля до единицы и, следовательно, радиус r изменя­ется от нуля до единицы. Если угол изменяется от 30 до 60, то радиус изменяется от единицы до нуля. Таким образом, при изменении угла  от 0 до 60 точка на плоскости описывает кривую, похожую на очертания лепестка, и возвращается в начало координат. Такие же лепестки получа­ются, когда угол изменяется в пределах от 120 до 180 и от 240 до 300 (рис. 5).

 

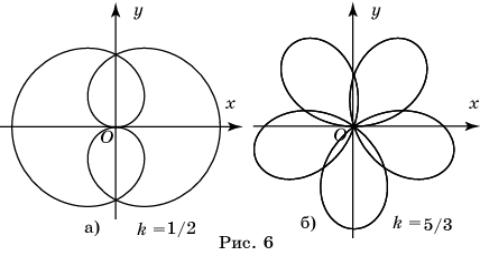
Розы – семейство кривых, полярные уравнения которых имеют вид , где a – положительное число, k – положительное рациональное число. Частным случаем роз является трилистник. Некоторые другие розы представлены на рисунках 6 а,б.

 

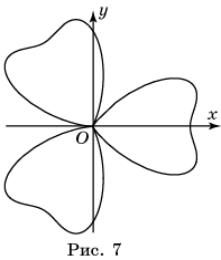
Лист щавеля.    С помощью уравнения в полярных координатах можно задавать самые различные формы цветов и листов. В качестве примера рассмотрим лист щавеля (рис. 7), задаваемого уравнением

 

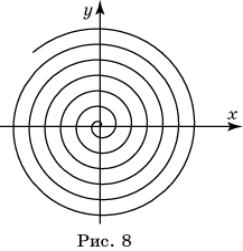
Спираль Архимеда - кривая, задаваемая уравнением

r = a φ,

где a - некоторое  фиксированное число.

Предположим, что a > 0, и построим график этой кривой. Если   φ = 0, то r = 0. Это означает, что кривая проходит через начало координат. Поскольку радиус неотрицателен, отрицательным углам φ никакие точки на кривой не соответствуют. Посмотрим, как изменяется радиус при увеличе­нии угла φ. В этом случае радиус r также будет увеличиваться. Напри­мер, при φ =  имеем r = a; при φ = π получаем r = a π, т.е. в два раза больше. При φ =  значение радиуса r будет в три раза больше и т.д. Соединяя плавной кривой полученные точки, изобразим кри­вую, которая называется спиралью Архимеда в честь ученого, ее открыв­шего и изучившего (рис. 8).

 

Геометрическим свойством, характеризующим спираль Архимеда, явля­ется постоянство расстояний между соседними витками. Каждое из них равно 2πa. Действительно, если угол φ увеличивается на 2π, т.е. точка делает один оборот против часовой стрелки, то радиус увеличивается на 2πa, что и составляет расстояние между соседними витками.

По спирали Архимеда идет звуковая дорожка на грампластинке. Туго свернутый рулон бумаги в профиль также представляет собой спираль Ар­химеда. Металлическая пластинка с профилем в виде половины витка архи­медовой спирали часто используется в конденсаторе переменной емкости. Одна из деталей швейной машины - механизм для равномерного наматывания ниток на шпульку - имеет форму спирали Архимеда.

Логарифмическая спираль. Логарифмическая спираль задается уравнением в полярных коорди­натах r =  , где a - некоторое фиксированное положительное число, φ  - угол, измеряемый в радианах (рис. 9).

 

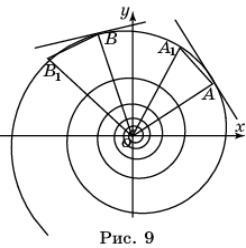
В отличие от спирали Архимеда, логарифмическая спираль бесконечна в обе стороны, так как угол φ может изменяться от - до +. При этом, если a > 1, то при увеличении угла радиус увеличивается, а если 0 < a < 1, то при увеличении угла радиус уменьшается.

Одним из основных свойств логарифмической спирали является то, что в любой ее точке угол между касательной к ней и радиусом-век­тором сохраняет постоянное значение.

Для доказательства этого воспользуемся тем, что касательную к кривой в точке А можно определить как предельное положение секущей АА₁ при А₁ стремящейся к А.

Пусть точки В, В₁ получены поворотом лучей ОА и ОА₁ на угол φ, (рис. 9). Тогда треугольники ОАА₁ и ОВВ₁ подобны, и поэтому углы ОАА₁ и ОВВ₁ равны. При А стремящейся к А₁ эти углы дадут углы между касательными и радиусами-векторами в точках А и В соответственно. Следовательно, угол между касательной и радиусом-вектором не зависит от положения точек на логарифмической спирали, т.е. сохраняет постоянное значение.

Именно это свойство логарифмической спирали используется в раз­личных технических устройствах. Например, при изготовлении вращающихся ножей, что позволяет сохранять при вращении постоянный угол резания. В гидротехнике по логарифмической спирали изгибают трубу, подводящую по­ток воды к лопастям турбины, благодаря чему напор воды используется с наибольшей производительностью.

Ночные бабочки, ориентируясь по параллельным лунным лучам, инс­тинктивно сохраняют постоянный угол между направлением полета и лучом света. Однако, если вместо луны они ориентируются на близко располо­женный источник света, например, на пламя свечи, то инстинкт их подво­дит. Сохраняя постоянный угол между направлением полета и источником света, они двигаются по скручивающейся логарифмической спирали и попа­дают в пламя свечи.

III. Кривые, заданные параметрическими уравнениями

Рассмотрим вопрос о том, как траектория движения точки описывается с помощью уравнений. Поскольку положение точки на плоскости однозначно определяется ее координатами, то для задания движения точки достаточно задать зависи­мости ее координат x, y от времени t, т.е. задать функции

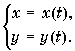
В этом случае для каждого момента времени t мы можем найти положение точки на плоскости.

Кривая на плоскости, описываемая точкой, координаты которой удовлетворяют этим уравнениям при изменении параметра t, называется параметрически заданной кривой на плоскости. Сами урав­нения называются параметрическими уравнениями.

График функции y=f(x) является частным случаем параметрически заданной кривой на плоскости. Параметрическими уравнениями в этом случае будут уравнения

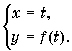
Если кривая задана уравнением в полярных координатах r = r(j), то, переходя к декартовым координатам, ее можно задать и параметрическими уравнениями

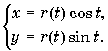
Окружность. Окружность радиуса R с центром в начале координат можно рассмат­ривать как параметрически заданную кривую на плоскости с параметричес­кими уравнениями

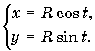
При изменении параметра t от нуля до 2π точка на окруж­ности делает один оборот против часовой стрелки, начиная и заканчивая в точке с координатами (R, 0). При дальнейшем увеличении параметра t точка будет многократно проходить по окружности в направлении против часовой стрелки.

Циклоида. Рассмотрим циклоиду – кривую, которая описывается точкой, закрепленной на окружности радиуса, катящейся по прямой (рис. 10).

 

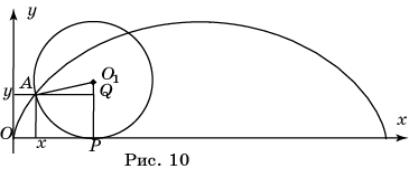
Найдем параметрические уравнения циклоиды. Пусть окружность катится по оси Ox и в начальный момент времени касается начала координат. Предположим, что окружность повернулась на некото­рый угол величины t. При этом точка касания O на окружности переместится в точку А. Поскольку дуга АР окружности при этом прокатилась по отрезку OР, то их длины равны, т.е. АР = OР = Rt. Для координат x, y точки А имеем

x = OP - AQ = Rt - R sin t = R(t - sin t),

y = O₁P -  O₁Q = R -  R cos t = R(1 - cos t)

и, таким образом, параметрическими уравнениями циклоиды являются урав­нения

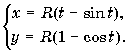
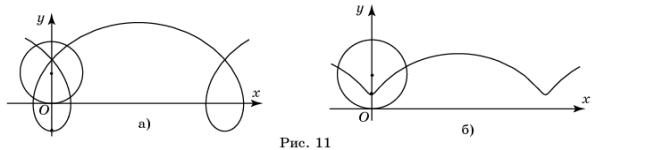
Удлиненная циклоида – траектория движения точки, закрепленной на продолжении радиуса окружности, катящейся по прямой (рис. 11,а).

 

Так же как и в случае с циклоидой, показывается, что параметрическими уравнениями удлиненной циклоиды являются

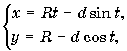
где d – расстояние от точки до центра окружности (d > R).

  Если d <R, то кривая называется укороченной циклоидой (рис. 11,б).

  Кардиоида – кривая, являющаяся траекторией движения точки, закрепленной на окружности, катящейся по окружности того же радиуса.

Обозначим через O центр неподвижной окружности радиуса a. В качестве полюса возьмем точку C на окружности, соответствующую начальному моменту времени. Пусть катящаяся окружность повернулась на угол t и точка C переместилась в точку C₁ (рис. 12).

 

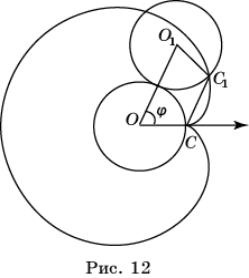
Четырехугольник OCC₁O₁ является равнобедренной трапецией. Следовательно, полярный угол точки C₁ будет равен t и

OC₁=2a(1-cos t).

Таким образом, уравнение кардиоиды будет иметь вид

r =2a(1-cos t).

Эпициклоиды.    Рассмотрим теперь ситуацию, когда точка закреплена на окружности радиуса r, катящейся по окружности радиуса R. Получаемые кривые подразделяются на эпициклоиды и гипоциклоиды в зависимости от того, располагается ли катящаяся окружность с внешней или внутренней стороны. Выведем уравнения эпициклоиды.

  Пусть центр O неподвижной окружности  является началом координат и точка A(0, R) соответствует начальному моменту времени. Предположим, что катящаяся с внешней стороны окружность повернулась на угол, равный t. При этом точка A переместилась в точку A₁(x,y) (рис. 13).

 

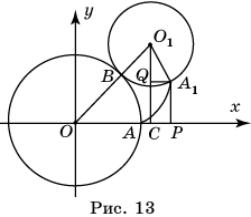
Обозначим отношение  через m. Из равенства длин дуг AB и A₁B следует, что угол AOB равен mt. Далее,

A₁O₁C = A₁O₁B - CO₁O = t – ( – mt)

и, следовательно,

sinA₁O₁C = sin(t – ( – mt)) = - cos(t+mt),

cosA₁O₁C = cos(t – ( – mt)) =  sin(t+mt).

Учитывая, что x = OP – OC, y = O₁C -  O₁Q, получаем параметрические уравнения эпициклоиды

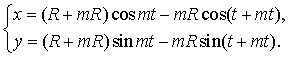
В частности, если m = 1, параметрические уравнения кардиоиды имеют вид

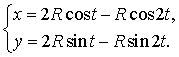
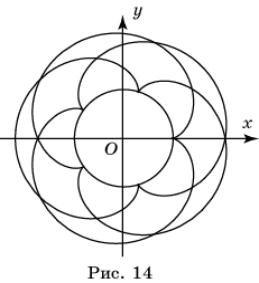
Еще один частный случай эпициклоиды показан на рисунке 14.

 

Аналогичным образом показывается, что если окружность радиуса r = mR катится по окружности радиуса R с внешней стороны, то точка, закрепленная на радиусе катящейся окружности на расстоянии h от центра, описывает кривую, задаваемую параметрическими уравнениями

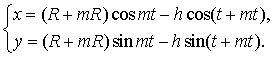
При этом, если h < R, то кривая называется укороченной эпициклоидой, а если h > R, то удлиненной эпициклоидой.

Гипоциклоиды. Так же как и для эпициклоиды показывается, что уравнения гипоциклоиды имеют вид

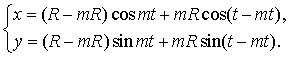
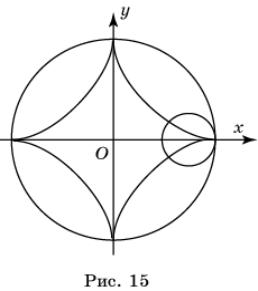
В частности, параметрические уравнения астроиды (рис. 15) (m=), имеют вид

 

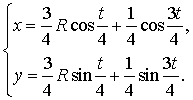
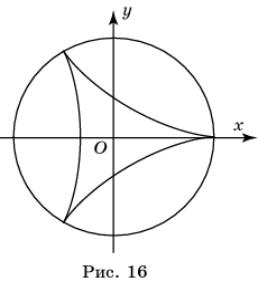
Параметрические уравнения кривой Штейнера (рис. 16) (m=), имеют вид

 

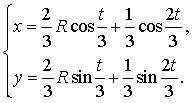
Еще один частный случай гипоциклоиды показан на рисунке 17.

 

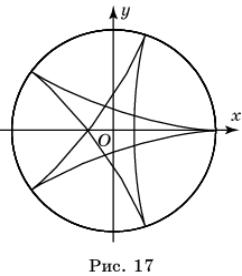
Если окружность радиуса r = mR катится по окружности радиуса R с внутренней стороны, то точка, закрепленная на радиусе катящейся окружности на расстоянии h от центра, описывает кривую, задаваемую параметрическими уравнениями

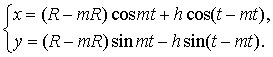
При этом, если h < R, то кривая называется укороченной гипоциклоидой, а если h  > R, то удлиненной гипоциклоидой.

 

 

         Упражнения

1. Нарисуйте кривую, задаваемую уравнением  r = sin 4 φ.

2. Нарисуйте кривую, задаваемую уравнением  r = cos φ.

3. Для  параболы  x²  = 4ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F(0, a) параболы. Переходя от де­картовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

.

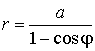4. Докажите, что уравнение

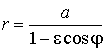
задает эллипс, если 0 <  < 1, и гиперболу, если  > 1.

5. Нарисуйте спираль Архимеда, заданную уравнением r = -φ. Чему равно расстояние между соседними витками этой спирали?

6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?

7. Нарисуйте гиперболическую спираль, задаваемую уравнением r = .

8. Нарисуйте спираль Галилея, которая задается уравнением       r = a² (a > 0). Она вошла в историю математики в XVII веке в связи с задачей нахождения формы кривой, по которой двигается свободно падающая в области экватора точка, не обладающая начальной скоростью, сообщаемой ей вращением земного шара.

9. Нарисуйте кривую, задаваемую уравнением r = ||.

10. Нарисуйте кривую, задаваемую уравнением r =.

11. Нарисуйте кривую, задаваемую уравнением r = .

12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.

 

ЛИТЕРАТУРА

1. Березин В. Кардиоида //Квант. – 1977. № 12.

2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.

3. Берман Г.Н. Циклоида. – М.: Наука, 1975.

4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. - / Приложение к журналу "Квант" № 2/2001.

5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.

6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. - / Популярные лекции по математике, выпуск 4.

7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.

8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.

9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.

10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.