§ 6. ЭЛЕМЕНТЫ
СТЕРЕОМЕТРИИ
1. Изобразите следующую геометрическую ситуацию: прямая a лежит в плоскости a, прямая b пересекает плоскость a в точке B, которая не принадлежит прямой a. Сделайте соответствующие записи с помощью математической символики.
2. Изобразите следующую геометрическую ситуацию: плоскости a и b пересекаются по прямой c, прямая l пересекает плоскости a и b соответственно в точках A и B, которые не принадлежат прямой c. Сделайте соответствующие записи с помощью математической символики.
3. Изобразите плоскости a, b, g, d, которые имеют общую прямую h.
4. Изобразите плоскости a, b, g, которые имеют общую точку H.
5. Пусть плоскости a, b пересекаются по прямой c. Плоскость g пересекает плоскости a и b соответственно по прямым a и b, причем a || c, b || c. Сделайте предположение о взаимном расположении прямых a и b.
6. Три вершины: а) треугольника; б) параллелограмма; в) пятиугольника принадлежат плоскости. Будет ли вся фигура лежать в этой плоскости?
7. Три точки: а) окружности; б) квадрата; в) трапеции принадлежат плоскости. Будет ли вся фигура лежать в этой плоскости?
8. Изобразите ромб ABCD, у которого: а) вершины A и D принадлежат плоскости a и плоскость ромба не совпадает с данной плоскостью; б) вершины A и C принадлежат плоскости a и плоскость ромба не совпадает с данной плоскостью; в) вершины B, C и O – точка пересечения диагоналей принадлежат плоскости a.
9. Какой многоугольник лежит в основании: а) призмы; б) пирамиды, если у нее 60 ребер?
10. Найдите сумму всех плоских углов: а) куба; б) октаэдра; в) пятиугольной пирамиды; г) десятиугольной призмы.
11. Сколько красок потребуется для правильной раскраски граней: а) призмы с четным числом боковых ребер; б) пирамиды с четным числом боковых ребер; в) призмы с нечетным числом боковых ребер; г) пирамиды с нечетным числом боковых ребер; д) бипирамиды с четным числом ребер в общем основании; е) бипирамиды с нечетным числом ребер в общем основании.
12. В правильном единичном тетраэдре ABCD найдите углы: а) ADB; б) ABC; в) CMD, где M – середина ребра AC; г) DHC, где H – середина ребра AB; д) AKB, где K – середина ребра CD.
13.
Найдите углы между пересекающимися диагоналями граней прямоугольного
параллелепипеда с измерениями 7 см, 7![]() см, 7 см.
см, 7 см.
14. Изобразите многогранники, имеющие: а) трехгранные; б) четырехгранные; в) пятигранные углы.
15. Сколько плоскостей можно провести через различные пары из: а) двух; б) трех; в) четырех; г) n параллельных прямых, никакие три из которых не лежат в одной плоскости?
16.
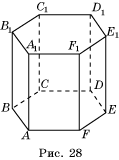
На рисунке 28 изображена правильная шестиугольная призма. Запишите все ребра:
а) параллельные ребру AB; б) параллельные ребру CC1; в) скрещивающиеся с ребром EF; г) скрещивающиеся с ребром BB1.
17. Изобразите четырехугольную пирамиду: а) выпуклую; б) невыпуклую.
18. Изобразите пятиугольную призму: а) выпуклую; б) невыпуклую.
19. Изобразите невыпуклый многогранник, все грани которого являются выпуклыми многоугольниками.
20. Будет ли треугольная бипирамида, составленная из правильных тетраэдров правильным многогранником. Почему?
21. Изобразите: а) куб; б) октаэдр; в) тетраэдр и двойственный к нему многогранник.
22. Найдите сумму плоских углов каждого правильного многогранника.
23. Найдите число двугранных углов каждого правильного многогранника.
24. Определите число вершин (В), ребер (Р) и граней (Г) усеченного: а) тетраэдра; б) гексаэдра; в) октаэдра; г) додекаэдра; д) икосаэдра.
25. Нарисуйте куб и полученный из него кубооктаэдр. Найдите ребро кубооктаэдра, если ребро куба равно 4 см. Определите число его вершин, ребер и граней.
26. Изобразите многогранник, который не является ни правильным, ни полуправильным, но все грани которого – правильные многоугольники.
27. Изобразите вписанный в куб: а) тетраэдр; б) многогранник Кеплера – “Stella Octangula”, найдите его ребро, если ребро куба равно a. Какой многогранник является пересечением тетраэдров, образующих многогранник Кеплера?
28. Нарисуйте куб и полученный из него усеченный куб Найдите ребро усеченного куба, если ребро куба равно b.
29. Поверхность какого многогранника напоминает поверхность футбольного мяча? Сколько у этого многогранника граней и какого они вида?
30. Изобразите многоугольник, который состоит из: а) четырех равных правильных треугольников; б) шести равных квадратов; в) восьми правильных треугольников и является разверткой соответственно правильного: а) тетраэдра; б) гексаэдра; в) октаэдра.
31. Изобразите многоугольник, который состоит из: а) четырех равных правильных треугольников; б) шести равных квадратов; в) восьми правильных треугольников и не является разверткой соответственно правильного: а) тетраэдра; б) гексаэдра; в) октаэдра.
32. Изобразите развертку правильной: а) треугольной призмы; б) четырехугольной пирамиды.
33. Изобразите развертку: а) правильной четырехугольной призмы; б) прямоугольного параллелепипеда; в) наклонного параллелепипеда.
34.
Изготовьте модели многогранников по разверткам, изображенным на рисунке 29. Как
они называются?

35. Каким образом из правильной n-угольной призмы получить соответствующий полуправильный многогранник – n-угольную антипризму, если: а) n = 4; б) n = 5; в) n = 6; г) n = m?
36. Какое число цветов нужно взять, чтобы правильно окрасить поверхность многогранников из задачи 34?
37. Изобразите развертку: а) цилиндра; б) конуса.
38. Найдите площадь поверхности: а) куба; б) правильного тетраэдра; в) октаэдра, г) икосаэдра, если их ребра равны 5 дм.
39. Найдите площадь: а) боковой; б) полной поверхности прямой треугольной призмы, если ее боковое ребро равно 15 см, а стороны основания равны 10 см, 12 см и 10 см.
40. Найдите площадь: а) боковой; б) полной поверхности правильной треугольной пирамиды, если ее боковое ребро равно 13 см, а апофема (высота боковой грани, проведенная к основанию) – 5 см.
41. Площадь боковой поверхности правильной треугольной призмы равна 480 см2. Высота призмы относится к стороне основания как 8 : 5. Найдите высоту призмы и сторону основания.
42. Сколько прямоугольных листов жести размером 2 м x 1 м понадобится для покрытия крыши башни, имеющей форму пирамиды с квадратным основанием, сторона которого равна 2,5 м, а длина ската крыши равна 3 м? Учесть, что на швы и обрезки пойдет 0,5 листа.
43. Сколько потребуется краски, чтобы покрасить печь цилиндрической формы, диаметр основания которой равен 15 дм, а высота 30 дм, если на один квадратный метр расходуется 200 г?
44. Высота конуса равна 24 см, радиус основания равен 7 см. Найдите площадь: а) боковой; б) полной поверхности конуса.
45. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см x 40 см?
46. Рассчитайте, какова должна быть площадь кабинета высотой 3,5 м для класса в 28 человек, если на каждого ученика нужно 7,5 м3 воздуха.
47.
Найдите объем и площадь поверхности правильной шестиугольной призмы, если
сторона основания относится к боковому ребру как 2 : 5 и радиус вписанной в
основание окружности равен ![]() см.
см.
48. Из медного листа толщиной 4 мм вырезали квадрат, правильные треугольник и шестиугольник, каждый многоугольник со стороной 10 см. Какие многогранники получились и как относятся их объемы?
49. Запишите формулу объема цилиндра: а) через его высоту (h) и длину окружности основания c; б) диаметр D основания которого равен его образующей.
50. Сколько чугунных труб длиной 4 м с наружным диаметром 33,5 мм и толщиной 3,25 мм можно погрузить на четырехтонный грузовик (удельный вес чугуна 7,3 г/см3)?
ОТВЕТЫ
6. а), б), в) Да. 7. а) Да; б), в) не обязательно. 9. а) 20-угольник; б) 30-угольник. 10. а) 2160°; б), в) 1440°; г) 6480°. 11. а), б)
3; в), г) 4; д) 2; е) 3. 12. а), б)
60°;
в) 90°;
г), д) ![]() . 13. 90°, 60°. 15. а) 1; б) 3; в) 6; г)
. 13. 90°, 60°. 15. а) 1; б) 3; в) 6; г) ![]() . 19. Например,
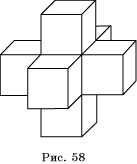
пространственный крест (рис. 58). 20.
Нет. 24. а) В = 4, Р = 6, Г = 4; б)
В = 8, Р = 12, Г = 6; в) В = 6, Р = 12, Г = 8; г) В = 20, Р = 30, Г = 12; д) В
= 12, Р = 30, Г = 20. 25.
. 19. Например,
пространственный крест (рис. 58). 20.
Нет. 24. а) В = 4, Р = 6, Г = 4; б)
В = 8, Р = 12, Г = 6; в) В = 6, Р = 12, Г = 8; г) В = 20, Р = 30, Г = 12; д) В
= 12, Р = 30, Г = 20. 25. ![]() см; В = 12, Р = 24, Г = 14. 26. Например, пятиугольная бипирамида, у которой все грани правильные
треугольники. 27.
см; В = 12, Р = 24, Г = 14. 26. Например, пятиугольная бипирамида, у которой все грани правильные
треугольники. 27. ![]() ; октаэдр. 28.
; октаэдр. 28. ![]() . 29. Усеченного
икосаэдра; Г = 32, из них 12 – правильные пятиугольники и 20 – правильные
шестиугольники. 34. а) Усеченный
тетраэдр; б) пятиугольная правильная призма; в) четырехугольная правильная
антипризма; г) восьмиугольная правильная пирамида. 38. а) 150 дм2; б)
. 29. Усеченного
икосаэдра; Г = 32, из них 12 – правильные пятиугольники и 20 – правильные
шестиугольники. 34. а) Усеченный
тетраэдр; б) пятиугольная правильная призма; в) четырехугольная правильная
антипризма; г) восьмиугольная правильная пирамида. 38. а) 150 дм2; б) ![]() дм2; в)
дм2; в) ![]() дм2; г)
дм2; г) ![]() дм2. 39.
а) 480 см2; б) 576 см2. 40. а) 180 см2; б)
дм2. 39.
а) 480 см2; б) 576 см2. 40. а) 180 см2; б) ![]() см2. 41.
16 см, 10 см. 42. 8 листов. 43. »2,8 кг. 44. а) 175pсм2; б) 224pсм2.
45. 90 досок. 46. 60 м2. 47. 120
см2. 41.
16 см, 10 см. 42. 8 листов. 43. »2,8 кг. 44. а) 175pсм2; б) 224pсм2.
45. 90 досок. 46. 60 м2. 47. 120![]() см3; 24(
см3; 24(![]() +10) см2. 48.
Четырехугольная, треугольная и шестиугольная правильные призмы; 4 :
+10) см2. 48.
Четырехугольная, треугольная и шестиугольная правильные призмы; 4 : ![]() : 6
: 6![]() . 49. а) V =
. 49. а) V = ![]() ; б) V =
; б) V =![]() . 50. 440.
. 50. 440.