§ 2. САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

 

57. Измерение площадей. Площадь прямоугольника

В а р и а н т  1

1°. Найдите площадь прямоугольника, если его стороны равны 1,1 дм и 19 см.

2°. Прямоугольник имеет площадь 256 см². Найдите сторону равновеликого ему квадрата.

3. Найдите стороны прямоугольника площади 144 дм², ели они относятся как 9 : 4.

4. В прямоугольном треугольнике MON  (ÐO = 90°) проведена высота OH. Докажите, что прямоугольник со сторонами MN и MH равновелик квадрату со стороной MO.

5*. Отрезок AB делится точками C и D соответственно на равные и неравные части. Докажите, что площадь прямоугольника со сторонами равными DA и DB равна разности площадей квадратов со сторонами, равными соответственно CB и CD.

6*. В четырехугольнике CDEF противоположные углы C и E – прямые, стороны ED и EF равны и высота EH = h, где HCF. Найдите площадь данного четырехугольника.

В а р и а н т  2

1°. Найдите площадь прямоугольника, если его стороны равны 1,7 дм и 5 см.

2°. Квадрат и прямоугольник со сторонами 16 см и 25 см равновелики. Найдите сторону квадрата.

3. Площадь прямоугольника равна 225 м², соседние стороны относятся как 1 : 9. Найдите его периметр.

4. В прямоугольном треугольнике DEF  (ÐD = 90°) проведена высота DP. Докажите, что квадрат со стороной DP равновелик прямоугольнику со сторонами EP и FP.

5*. Каким образом следует разделить отрезок MN точкой H, чтобы прямоугольник со сторонами равными HM и HN имел наибольшую площадь?

6*. Постройте квадрат, площадь которого в два раза больше площади данного квадрата.

 

58. Площадь параллелограмма

В а р и а н т  1

1°. Найдите площадь параллелограмма, если его стороны равны 11 см и 12 см, а один из углов равен 30°.

2°. Стороны параллелограмма равны 16 см и 8 см. Высота, опущенная на первую сторону, равна 6 см. Найдите вторую высоту параллелограмма.

3. Периметр параллелограмма равен 72 дм, высоты равны 3 дм и 9 дм. Найдите площадь параллелограмма.

4. Найдите формулу для вычисления площади параллелограмма по его периметру, равному P, и расстояниям d₁, d₂ от точки пересечения диагоналей до сторон.

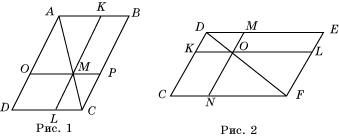
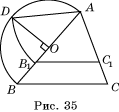
5*. На рисунке 1 изображен параллелограмм ABCD, точка M – произвольная точка диагонали AC, OP || AB, KL || BC. Определите вид четырехугольников MLDO и MKBP и докажите, что они равновелики.

6*. В прямоугольник, стороны которого относятся как 3 : 4 вписан четырехугольник, сторонами которого являются середины сторон прямоугольника. Найдите площадь этого четырехугольника, если одна из его сторон равна 15 см.

В а р и а н т  2

1°. Найдите площадь параллелограмма, если его стороны равны 6 см и 8 см, а один из углов равен 45°.

2°. Площадь параллелограмма равна 28 см², стороны – 7 см и 8 см. Найдите его углы.

3. Площадь параллелограмма равна 72 дм². Расстояния от точки пересечения его диагоналей до сторон равны 3 дм и 9 дм. Найдите периметр параллелограмма.

4. Найдите формулу для вычисления площади параллелограмма по его периметру, равному 2p, и двум его высотам h₁, h₂.

5*. В параллелограмме CDEF (рис. 2) точка O – произвольная точка диагонали DF, через нее проведены отрезки KL, параллельный CF, и MN, параллельный EF. Определите вид четырехугольников OLEM и OKCN и докажите, что они равновелики.

6*. Через вершины четырехугольника проведены прямые, параллельные его соответствующим диагоналям. Найдите площадь четырехугольника, который образуется этими прямыми, если площадь данного четырехугольника равна 2Q.

 

59. Площадь треугольника

В а р и а н т  1

1°. Найдите площадь прямоугольного треугольника с катетами 5 дм и 12 см.

2°. Найдите площадь треугольника, если две его стороны равны a и b и угол между ними равен 60°.

3. Может ли площадь треугольника со сторонами 7 см и 8 см быть равной: а) 56 см²; б) 28 см²; в) 14 см²? Ответ поясните.

4. Найдите геометрическое место вершин C равновеликих треугольников, имеющих общую сторону AB.

5*. Разделите данный прямоугольник на три равновеликие части прямыми, выходящими из одной его вершины.

6*. Найдите площадь треугольника, если его медианы равны 6 см, 15 см и 18 см.

В а р и а н т  2

1°. Найдите площадь равностороннего треугольника со стороной 2 см.

2°. Найдите площадь треугольника, если две его стороны равны m и n и угол между ними равен 30°.

3. Может ли площадь треугольника со сторонами 4 дм и 12 дм быть равной: а) 12 дм²; б) 24 дм²; в) 48 дм²? Ответ поясните.

4. Постройте треугольник, площадь которого равна сумме площадей двух треугольников, имеющих одинаковую высоту.

5*. Разделите данный параллелограмм на пять равновеликих частей прямыми, выходящими из одной его вершины.

6*. Медианы треугольника равны 12 см, 9 см и 6 см. Найдите его площадь.

 

60. Площадь трапеции

В а р и а н т  1

1°. Высота трапеции равна 1 дм, площадь – 85 см². Найдите ее среднюю линию.

2°. В трапеции KLMN с основаниями LM и NK диагонали пересекаются в точке P. Найдите пары равновеликих треугольников.

3. Найдите площадь равнобедренной трапеции с основаниями 12 см и 8 см и углом 135°.

4. Докажите, что если в трапеции середину одной боковой стороны соединить с концами другой боковой стороны, то площадь полученного треугольника будет равна половине площади трапеции.

5*. В трапеции OPHQ основания PH и OQ равны соответственно p и q (p < q). Высота трапеции равна h, OR = r, где точка r принадлежит OQ. Найдите на PH точку S, чтобы отрезок RS разделил трапецию на две части, площади которых относятся как m : n.

6*. Трапеция разделена диагоналями на четыре треугольника. Площади треугольников, прилегающих к основаниям равны S₁ и S₂. Найдите площади двух других треугольников.

В а р и а н т  2

1°. Основания трапеции равны 1,3 дм и 1,1 дм, площадь равна 48 см². Найдите ее высоту.

2°. В трапеции EFGH (EF || GH) диагонали пересекаются в точке M. Найдите пары равновеликих треугольников.

3. Найдите площадь прямоугольной трапеции с основаниями 5 см и 8 см, большая боковая сторона которой составляет с основанием угол 135°.

4. Докажите, что площадь трапеции равна произведению одной из ее боковых сторон на перпендикуляр, опущенный на нее из середины другой боковой стороны.

5*. Трапеция KLMN (KL || MN) разделена отрезком EF, параллельным KN, где точки E, F принадлежат сторонам трапеции соответственно KL и MN, на две части EFNK и EFML, отношение площадей которых равно m : n. Найдите отрезок KE, если KL = a, MN = b.

6*. Трапеция разделена диагоналями на четыре треугольника. Площади треугольников, прилегающих к основаниям равны Q₁ и Q₂. Найдите площади двух других треугольников.

 

61. Площадь многоугольника

В а р и а н т  1

1°. Найдите площадь квадрата, вписанного в окружность радиуса R.

2°. Найдите площадь правильного шестиугольника со стороной a.

3. Около окружности, диаметр которой равен 16 см, описан многоугольник, площадь которого равна 192 см². Найдите периметр многоугольника.

4. Найдите площадь четырехугольника, если его диагонали равны 17 см и 9 см, а угол между ними равен 60°.

5*. Равносторонний треугольник со стороной 1 повернут вокруг своего центра на угол 60°. Найдите площадь пересечения исходного треугольника и повернутого.

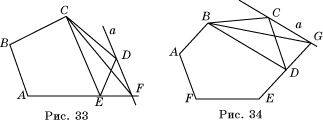
6*. Постройте четырехугольник, равновеликий данному пятиугольнику ABCDE.

В а р и а н т  2

1°. Найдите площадь квадрата, описанного около окружности радиуса r.

2°. Найдите площадь правильного треугольника со стороной b.

3. Окружность радиуса 15 см вписана в правильный многоугольник со стороной 3 см. Найдите число сторон данного многоугольника, если его площадь равна 450 см­_­­­­².

4. Диагонали четырехугольника равны 9 см и 81 см. Угол между ними равен 135°. Найдите площадь данного четырехугольника.

5*. Квадрат со стороной 1 повернут вокруг его центра на угол 45°. Найдите площадь пересечения исходного квадрата и повернутого.

6*. Постройте пятиугольник, равновеликий данному шестиугольнику ABCDEF.

 

62. Площадь круга и его частей

В а р и а н т  1

1°. Площадь круга равна 289p см². Найдите его диаметр и длину окружности.

2°. Найдите площадь кольца, если радиусы его окружностей равны 19 мм и 28 мм.

3. Даны две концентрические окружности, хорда большей из них, касающаяся меньшей окружности, равна 20 см. Найдите площадь кольца, ограниченного этими окружностями.

4. Найдите площадь сегмента круга радиуса R, если его угол равен 120°.

5*. Постройте полукруг, равновеликий данному кругу.

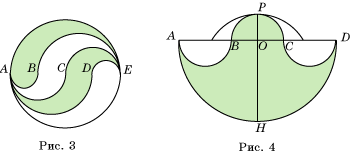
6*. На рисунке 3 отрезки AB, BC, CD и DE равны. На отрезках AB, AC, AD, AE и DE, CE, BE, AE, как на диаметрах построены полуокружности. Докажите, что четыре образовавшиеся непересекающихся криволинейные фигуры равновелики.

В а р и а н т  2

1°. Длина окружности равна 38p см. Найдите ее диаметр и площадь соответствующего круга.

2°. Найдите площадь кольца, если длины его окружностей равны 24 мм и 18 мм.

3. Даны две концентрические окружности. Найдите хорду большей окружности, которая касается меньшей окружности, если площадь соответствующего круга равна 400p дм².

4. Найдите площадь сегмента, если его хорда равна a и дуга окружности содержит 90°.

5*. Постройте круг, равновеликий данному полукругу.

6*. На рисунке 4 отрезки AB и CD равны, точка O – середина отрезка AD. На отрезках AB, CD, AD, BC, как на диаметрах проведены полуокружности. Докажите, что фигура, ограниченная этими полуокружностями, равновелика кругу с диаметром PH, где PH – перпендикуляр к AD, проходящий через точку O.

 

63. Площади подобных фигур

В а р и а н т  1

1°. Площадь треугольника равна 36 см². Найдите площадь треугольника, образованного его средними линиями.

2°. Периметры подобных многоугольников равны 120 см и 720 см. Найдите отношение их площадей.

3. Сумма площадей трех подобных треугольников равна 413 дм², их периметры относятся как 1 : 3 : 7. Найдите площадь каждого многоугольника.

4. В окружности с центром O проведены диаметр EF, хорды EG, FG, причем последняя стягивает дугу 60°. Касательная к окружности, проведенная через точку G, пересекает прямую EF в точке M. Найдите отношение площадей треугольников MGF и MGE.

5*. Постройте треугольник, площадь которого в два раза меньше площади данного треугольника.

6*. Каждая сторона квадрата повернута на 30° вокруг одной из своих вершин, как показано на рисунке 5. Найдите отношение сторон и площадей данного квадрата и квадрата, образованного его повернутыми сторонами.

В а р и а н т  2

1°. Площадь треугольника равна 64 см². Найдите площадь треугольника, отсеченного от него средней линией.

2°. Площади подобных многоугольников равны 810 см² и 90 см². Найдите отношение их периметров.

3. В прямоугольном треугольнике катеты относятся как 3 : 4, высота делит его на два треугольника, разность площадей которых равна 56 дм². Найдите площадь данного треугольника.

4. В окружности проведены две непересекающиеся хорды KL и MN, которые стягивают дуги соответственно 90° и 120°. Прямые MK и MN пересекаются в точке P. Найдите площади треугольников PKL и PMN, если их сумма равна 200 см².

5*. Постройте треугольник, площадь которого в два раза больше площади данного треугольника.

6*. На рисунке 6 ABCD – квадрат. Точки A₁, A₂, B₁, B₂, C₁, C₂, D₁, D₂ делят его соответствующие стороны на три равные части. Найдите отношение площадей данного квадрата и четырехугольника EFGH.

 

64. Изопериметрическая задача

В а р и а н т  1

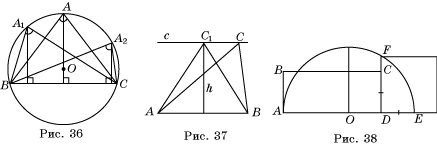
1°. Определите наибольшую сторону треугольника BCD, если: а) угол B – тупой; б) угол C – прямой; в) углы B и D – острые.

2°. Какова наибольшая площадь треугольника со сторонами 37 см и 46 см?

3. Среди всех треугольников, имеющих одну и ту же сторону и равные углы, ей противолежащие, найдите треугольник наибольшей площади.

4. Среди всех равновеликих треугольников с данной стороной найдите треугольник, который имеет наибольший угол, противолежащий этой стороне.

5*. Докажите, что среди всех изопериметрических треугольников с данной стороной, наибольшую площадь имеет равнобедренный треугольник, у которого данная сторона является основанием.

6*. Докажите, что из всех равновеликих прямоугольников наименьший периметр имеет квадрат.

В а р и а н т  2

1°. Определите наименьшую и наибольшую стороны прямоугольного треугольника DEF (ÐE = 90°), если ÐF = 38°.

2°. Треугольник имеет стороны 19 см и 27 см. В каких пределах заключена его площадь?

3. Найдите четырехугольник наибольшей площади, вписанный в круг.

4. Докажите, что среди всех треугольников, имеющих по равному углу и равной высоте, выходящей из этого угла, наибольшую площадь имеет равнобедренный треугольник.

5*. Докажите, что среди всех равновеликих треугольников, имеющих общую сторону, наименьший периметр имеет равнобедренный треугольник, у которого основание равно данной стороне.

6*. Докажите, что если квадрат и треугольник равновелики, то периметр треугольника больше периметра квадрата.

 

65. Равносоставленность и задачи на разрезание

В а р и а н т  1

1°. Разрежьте треугольник по прямой, проходящей через его вершину, на два равновеликих треугольника.

2°. Разрежьте треугольник на шесть равновеликих треугольников

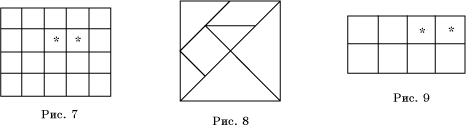
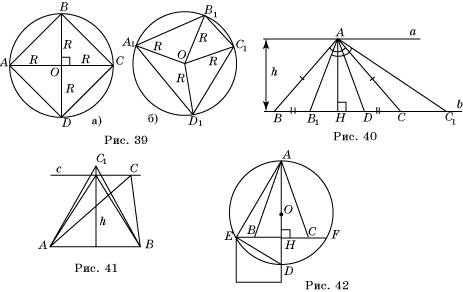
3. Разрежьте фигуру, изображенную на рисунке 7, на две равные части, чтобы в каждой из них была звездочка.

4. Сложите: а) прямоугольник; б) равнобедренный прямоугольный треугольник из семи частей квадрата, изображенных на рисунке 8.

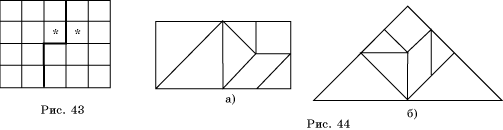
5*. Разрежьте прямоугольный треугольник, имеющий угол 30°, на четыре равных треугольника.

6*. Докажите, что ромб равносоставлен с равновеликим ему квадратом.

В а р и а н т  2

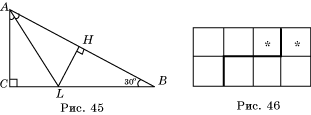
1°. Разрежьте треугольник по прямым, проходящим через его вершину, на три равновеликих треугольника.

2°. Разрежьте параллелограмм на 12 равных треугольников.

3. Разрежьте фигуру, изображенную на рисунке 9, на две равные части, чтобы в каждой из них была звездочка.

4. Сложите: а) параллелограмм; б) равнобедренную трапецию из семи частей квадрата, изображенных на рисунке 8.

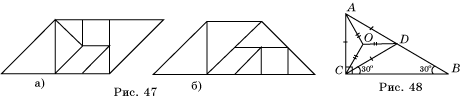
5*.  Разрежьте прямоугольный треугольник, имеющий угол 30°, на четыре подобных треугольника.

6*. Докажите, что прямоугольник равносоставлен с равновеликим ему параллелограммом.

 

66. Прямоугольная система координат

В а р и а н т  1

1°. Изобразите прямоугольную систему координат и отметьте точки K(1, -3) и L(-5, 0). Найдите координаты точек H и P – оснований перпендикуляров, опущенных соответственно из точки K на ось Ox и из точки L на ось Oy.

2°. Найдите координаты середины отрезка MN, если: а) M(0, -8), N(11, -4); б) M(3, -10), N(-13, 3).

3. Найдите координаты точки пересечения отрезка AB с осью абсцисс, если A(3, -2), B(6, 5).

4. Найдите координаты точки, симметричной точке E(-4, 9) относительно: а) начала координат; б) оси ординат; в) оси абсцисс.

5*. Найдите ГМТ координатной плоскости, для которых |x| > 5.

6*. Найдите ГМТ координатной плоскости, для которых x² + y² > 5.

В а р и а н т  2

1°.  Изобразите прямоугольную систему координат и отметьте точки M(-2, 1) и N(3, 0). Найдите координаты точек E и F – оснований перпендикуляров, опущенных соответственно из точки M на ось Oy и из точки N на ось Ox.

2°. Найдите координаты середины отрезка KL, если: а) K(-5, 6), L(11, -17); б) K(0,5, 8), L(0,3, -12).

3. Найдите координаты точки пересечения отрезка CD с осью Oy, если C(6, 4), D(-2, -5).

4. Найдите координаты точки, симметричной точке Q(6, -4) относительно: а) оси Ox; б) оси ординат; в) начала координат.

5*. Найдите ГМТ координатной плоскости, для которых |y| £ 4.

6*. Найдите ГМТ координатной плоскости, для которых x² + y² < 3.

 

67. Расстояние между точками. Уравнение окружности

В а р и а н т  1

1°. Найдите расстояние между точками P и Q, если P(1, 5), Q(-8, 9).

2°. Напишите уравнение окружности с центром в точке M(0, -13) и радиусом 11.

3. Определите вид треугольника BCD и длину его высоты DH, если B(0, 2), C(6, 4), D(5, -3).

4. Даны точки K(-7, 2) и L(3, 6). Найдите координаты точки, принадлежащей оси ординат и одинаково удаленной от данных точек.

5*. Даны три точки R(0, 10), S(7, -4), T(5, 0). Принадлежат ли они одной прямой?

6*. Найдите точки, одинаково удаленные от координатных прямых и точки с координатами (-6, 12).

В а р и а н т  2

1°. Найдите длину отрезка GH, если G(5, -4), H(-1, -8).

2°. Напишите уравнение окружности с центром в точке K(-11, 0) и радиусом 12.

3. Определите вид треугольника CDE и длину его высоты EP, если C(-10, -2), D(-4, 2), E(-9, 3).

4. Даны точки M(6, -5) и N(-6, 2). Найдите координаты точки, принадлежащей оси абсцисс и одинаково удаленной от данных точек.

5*. Является ли отрезок QP, где Q(-5, 4), P(-3, -6) хордой окружности x² + y² + 6x – 8y + 21 = 0? Изобразите данную геометрическую ситуацию.

6*. Найдите точки, одинаково удаленные от точки A(8, -4) и осей абсцисс и ординат.

 

68. Векторы. Сложение векторов

В а р и а н т  1

1°. Дан квадрат ABCD. Запишите векторы, равные вектору .

2°. В треугольнике EFG от точки M – его центроида, отложите векторы, равные векторам , , , , где G₁ – середина стороны EF.

3. Найдите сумму векторов: а) ; б) .

4. Задайте векторы  и . Постройте: а) ; б) ; в) .

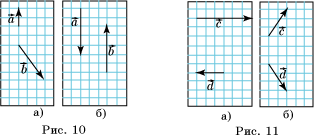
5*. На рисунке 10 заданы векторы  и . От произвольно выбранных точек плоскости в каждом случае отложите векторы , , .

6*. Докажите, что для любых векторов  и  выполняется неравенство .

В а р и а н т  2

1°. Дан ромб ABCD. Запишите векторы, равные вектору .

2°. В треугольнике KLM от точки G – его центроида, отложите векторы, равные векторам , , , , где KL₁ =ML₁.

3. Найдите сумму векторов: а) ; б) .

4. Задайте векторы  и . Постройте: а) - + ; б)  - ; в)  - .

5*. На рисунке 11 заданы векторы  и . От произвольно выбранных точек плоскости в каждом случае отложите векторы: а) ; б) ; в) .

6*. Верно ли неравенство ?

 

69. Умножение вектора на число

 В а р и а н т  1

1°. Задайте ненулевой вектор  и постройте векторы: а) 3; б) ; в) .

2°. В параллелограмме BCDE диагонали пересекаются в точке P. Найдите: а) ; б) ; в) ; г) .

3. В треугольнике KLM медианы KK₁, LL₁, MM₁ пересекаются в точке G. Выразите через векторы  и  векторы: а) ; б) ; в) ; г) .

4. Дан ненулевой вектор . При каких значениях m: а) векторы  и m сонаправлены (т.е. при откладывании от одной точки лежат на одной прямой и имеют одно направление); б) верно неравенство |m| < ||?

5*. Запишите в векторной форме условия того, что точка O лежит между точками A и B.

6*. Докажите, что , где M – произвольная точка плоскости, O – середина отрезка KL.

В а р и а н т  2

1°. Задайте ненулевой вектор  и постройте векторы: а)2; б) ; в) .

2°. В прямоугольнике DEFG диагонали пересекаются в точке M. Найдите: а) ; б) ; в) ; г) .

3. В треугольнике OPQ точка M – центроид, O₁, P₁, Q₁ – середины соответствующих сторон PQ, OQ, OP. Выразите через векторы  и  векторы: а) ; б) ; в) ; г) .

4. Дан ненулевой вектор . При каких значениях n: а) векторы  и n противоположно направлены (т.е. при откладывании от одной точки лежат на одной прямой и имеют противоположные направления); б) верно неравенство |n| > ||?

5*. Запишите в векторной форме условия того, что точка O является точкой пересечения диагоналей четырехугольника ABCD.

6*. Докажите, что , где O – произвольная точка плоскости, KLN – данный треугольник, M – его центроид.

 

70. Координаты вектора

В а р и а н т  1

1°. Найдите координаты вектора , если: а) ; б) ; в) ; г) .

2°. Найдите координаты вектора , если: а) E(1, 2), F(2, 1); б) E(-2, 0), F(3, 1); в) E(10, -3), F(0, -9); г) E(-8, -5), F(12, -18).

3. Найдите координаты точки H, если: а) , G(5, -7); б) G(0, 25), .

4. Точка P делит отрезок MN в отношении 1 : 4. Найдите координаты вектора , если .

5*. Докажите с помощью векторов теорему о средней линии треугольника.

6*. Докажите, что отрезок, соединяющий середины оснований трапеции, проходит через точку пересечения ее диагоналей.

В а р и а н т  2

1°. Найдите координаты вектора , если: а) ; б) ; в) ; г) .

2°. Найдите координаты вектора , если: а) G(0, 1), H(0, -1); б) G(5, -4), H(-10, 7); в) G(0, -15), H(24, 5); г) G(4, -9), H(16, 0).

3. Найдите координаты точки A, если: а) , B(15, -21); б) B(0, -16), .

4. Отрезок KL разделен точкой E в отношении 2 : 3. Найдите координаты вектора , если .

5*. Точка M делит отрезок AA₁ в отношении 2 : 1. Докажите, что для произвольной точки X выполняется равенство: .

6*. Точки E и F делят диаметр окружности на три равные части. Докажите, что сумма квадратов расстояний от любой точки этой окружности до данных точек есть величина постоянная.

 

71. Скалярное произведение векторов

В а р и а н т  1

1°. Найдите скалярное произведение двух единичных векторов, угол между которыми равен 30°.

2°. Дан равносторонний треугольник ABC со стороной, равной 4 см. Найдите: а) ; б) ; в) , где B_1­ – середина стороны AC.

3. Определите вид треугольника DEF, если D(-7, 2), E(2, 5), F(4, 10).

4. Даны векторы (0, -5) и (-2, 8). При каком значении x векторы  и 2 - 3x перпендикулярны.

5*. Вычислите работу, которую производит сила (15, -9), когда точка ее приложения перемещается, двигаясь прямолинейно, из положения Z₁(-5, 18) в положение Z₂(-3, 15).

6*. На сторонах треугольника XYZ внешним образом построены квадраты XYKP и YZGL (рис. 12). Точка M – середина KL. Докажите, что прямые XZ и YM перпендикулярны.

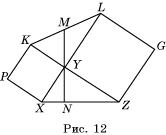
В а р и а н т  2

1°. Найдите скалярное произведение двух векторов длины 2, угол между которыми равен 45°.

2°. Дан единичный квадрат ABCD. O – точка пересечения его диагоналей. Найдите: а) ; б) ; в) .

3. Определите вид треугольника MNK, если M(-10, -5), N(-5, 5), K(6, 7).

4. Даны векторы (2, 0) и (-3, 5). При каком значении y векторы 2 и y - 4 перпендикулярны.

5*. Вычислите работу, которую производит сила (3, -9), когда точка ее приложения перемещается, двигаясь прямолинейно, из положения A(5, -8) в положение B(15, -12).

6*. Докажите, что высоты треугольника или их продолжения пересекаются в одной точке.

 

72. Уравнение прямой

В а р и а н т  1

1°. Запишите уравнение прямой, проходящей через точку H(-5, 6), перпендикулярную оси абсцисс.

2°. Постройте прямую 2x – y + 4 = 0 и найдите ее точки пересечения с координатными осями.

3. Запишите уравнение прямой, проходящей через точки M(1, -2) и N(3, 0). Найдите координаты ее вектора нормали.

4. Найдите координаты точки пересечения прямых x – y – 10 = 0 и 6x + 7y – 21 = 0.

5*. Запишите уравнения перпендикулярных прямых, пересекающихся в точке P(-5, -2), если одной из них принадлежит точка Q(-2, 2,5).

6*. Запишите уравнение прямой, которая проходит через точку S(11, 5) и касается окружности x² + y² + 12x – 6y + 41 = 0.

В а р и а н т  2

1°. Запишите уравнение прямой, проходящей через точку P(7, -4), перпендикулярную оси ординат.

2°. Постройте прямую x + 6y – 12 = 0 и найдите ее точки пересечения с координатными осями.

3. Запишите уравнение прямой, проходящей через начало координат и точку P(-8, 12). Найдите координаты ее вектора нормали.

4. Найдите координаты точки пересечения прямых 4x – 3y + 24 = 0 и 2x + 3y – 6 = 0.

5*. Запишите уравнение окружности, которая проходит через точку M(-1, 6) и касается оси: а) абсцисс; б) ординат.

6*. Запишите уравнение прямой, которая проходит через точку R(13, -14) и касается окружности x² + y² – 18x + 12y + 101 = 0.

 

73. Аналитическое задание фигур на плоскости

В а р и а н т  1

1°. Найдите фигуру, которая задается неравенством x 0.

2°. Нарисуйте фигуру, задаваемую неравенствами: 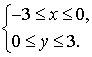 Как она называется.

3. Нарисуйте фигуру, которая задается неравенствами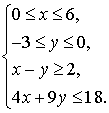

4. На рисунке 13 изображен шестиугольник ABCDEF. Запишите неравенства, которые его задают.

5*. Для параболы, заданной уравнением y = x² – 2x – 1, найдите координаты ее фокуса и уравнение директрисы.

6*. Напишите уравнение эллипса, проходящего через точку M(1, ), сумма расстояний от которой до фокусов эллипса равна 10.

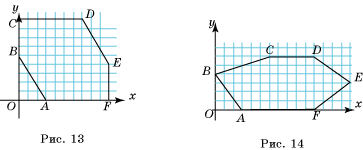
В а р и а н т  2

1°. Найдите фигуру, которая задается неравенством y £ 0.

2°. Нарисуйте фигуру, задаваемую неравенствами: 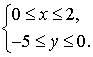 Как она называется.

3. Нарисуйте фигуру, которая задается неравенствами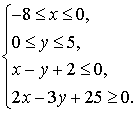

4. На рисунке 14 изображен шестиугольник EABCDF. Запишите неравенства, которые его задают.

5*. Вершина параболы расположена в начале координат. Уравнение директрисы имеет вид y – 2 = 0. Найдите координаты ее фокуса и запишите ее уравнение.

6*. Найдите координаты фокусов и точек пересечения с осью ординат гиперболы, заданной уравнением 16x² – y² + 4y – 4 = 16.

 

74*. Задачи оптимизации

В а р и а н т  1

1°. Нарисуйте фигуру, координаты точек которой удовлетворяют неравенству: а) x  0; б) y < 5.

2°. Нарисуйте фигуру, координаты точек которой удовлетворяют неравенству: а) x – y  1; б) 3x + 2y > 0.

3. Нарисуйте фигуру, координаты точек которой удовлетворяют неравенству: а) |x| < 2; б) |y| ³ 5.

4. Нарисуйте фигуру, координаты точек которой удовлетворяют системе неравенств: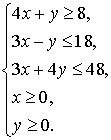

      5*. Найдите наибольшее значение функции F=3x+3y при условии

     

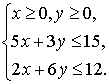
6*. Для изготовления полки нужно вырезать из фанеры одну заготовку для задней стенки (деталь А), две заготовки для боковинок (деталь Б) и три одинаковых заготовки для верхней, средней и нижней горизонтальных панелей (деталь В). Имеющиеся на мебельном комбинате листы фанеры таковы, что при первом способе раскроя из одного листа можно изготовить одну деталь типа А, четыре типа Б и восемь типа В, а при втором способе три детали типа А, две типа Б и две типа В. Можно ли, имея 180 листов фанеры, изготовить 200 полок? Как осуществить раскрой материала, чтобы было использовано наименьшее число листов фанеры?

В а р и а н т  2

1°. Нарисуйте фигуру, координаты точек которой удовлетворяют неравенству: а) y < 0; x  -1.

2°. Нарисуйте фигуру, координаты точек которой удовлетворяют неравенству: а) 2x – y < 3; б) x + 4y ³ -5.

3. Нарисуйте фигуру, координаты точек которой удовлетворяют неравенству: а) |x| ³ 4; б) |y| < 2.

4. Нарисуйте фигуру, координаты которой удовлетворяют системе неравенств:

     

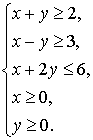
      5. Найдите наименьшее значение функции F=3x+4y при условии

     

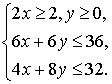
      6*. Для изготовления полки нужно вырезать из фанеры одну заготовку для задней стенки (деталь А), две заготовки для боковинок (деталь Б) и три одинаковых заготовки для верхней, средней и нижней горизонтальных панелей (деталь В). Имеющиеся на мебельном комбинате листы фанеры таковы, что при первом способе раскроя из одного листа можно изготовить одну деталь типа А, четыре типа Б и восемь типа В, а при втором способе три детали типа А, две типа Б и две типа В. Можно ли, имея 180 листов фанеры, изготовить 200 полок? Как осуществить раскрой материала, чтобы было использовано наименьшее число листов фанеры?

 

75*. Тригонометрические функции произвольного угла

В а р и а н т  1

1°. Постройте окружность с центром в начале координат и изобразите точку, получающуюся из точки с координатами (1, 0) поворотом на: а) 30°; б) 90°; в) 150°; г) 420°; д) -135°.

2°. Определите, углом какой четверти является угол a, если: а) a = 190°; б) a = 100°; в) a  = - 45°; г) a = 500°; д) a = 1080°.

3. Найдите значение выражения: а) 2cos 0° - 4sin 90° + 5tg 180°; б) 2cos 60° + cos 30°; в) 2sin 30° + 6cos 60° - 4 tg 45°; г) 3tg 45°tg 60°.

4. Найдите значение выражения: а) sin(-30°) + cos(-60°); б) cos 135° + sin(-210°); в) 2sin 120°tg 300°; г) 4sin(-150°)cos 300°tg 240°.

5*. Решите уравнение: а) sin a = 1; б) tg b = 0.

6*. Отметьте на единичной окружности дуги, соответствующие углам g, для которых: а) cosg  0; б) |sing| <.

В а р и а н т  2

1°. Постройте окружность с центром в начале координат и изобразите точку, получающуюся из точки с координатами (1, 0) поворотом на: а) 45°; б) 135°; в) 270°; г) 540°; д) -150°.

2°. Определите, углом какой четверти является угол b, если: а) b= 60°; б) b= 187°; в) b  = 235°; г) b= -118°; д) b= 2160°.

3. Найдите значение выражения: а) 2tg 0° - 3cos 270° + 5sin 0°; б) 2sin 30° - ctg 45°; в) 4sin 45° - cos 30° + 8 tg 60°; г) 4ctg 30°cos 60°.

4. Найдите значение выражения: а) sin(-60°) + cos(-30°); б) cos (-180°) + cos 300°; в) 6cos(-240°)ctg 210°; г) 8sin(-30°)cos 60°+ tg(135°)ctg(-225°).

5*. Решите уравнение: а) sin b = -1; б) ctg a = 0.

6*. Отметьте на единичной окружности дуги, соответствующие углам , для которых: а) sin> 0; б) |cos|.

 

76. Полярные координаты

В а р и а н т  1

1°. Изобразите в полярных координатах точки A(3, 0), B(8, ) и E(5, -).

2°. Полярные координаты точки равны: а) (1, p); б) (2, -). Найдите ее декартовы координаты.

3. Изобразите ГМТ на плоскости, полярные координаты которых удовлетворяют равенству: а) r – 1 = 0; б) = -.

4. Найдите полярное уравнение прямой x = -2.

5*. Запишите уравнение спирали Архимеда, если расстояние между ее соседними витками равно 3.

6*. Определите расстояние между точками B(1, ) и D(2, -).

В а р и а н т  2

1°. Изобразите в полярных координатах точки B(2, ), D(3, 0) и F(7, -).

2°. Декартовы координаты точки равны: а) (-1, 1); б) (2, -2). Найдите ее полярные координаты.

3. Изобразите ГМТ на плоскости, полярные координаты которых удовлетворяют равенству: а) j = ; б) r = 2.

4. Найдите полярное уравнение прямой y = -1.

5*. Запишите уравнение спирали Архимеда, если расстояние между ее соседними витками равно .

6*. Определите расстояние между точками A(3, -) и C(1, p).

Замечание. Задачи по теме «Начала стереометрии» вы найдете в § 6 данного пособия.

 

ОТВЕТЫ

57

В а р и а н т  1. 1. 209 см² . 2. 16 см. 3. 18 дм, 8 дм. 6*. h².

В а р и а н т  2. 1. 85 см². 2. 20 см. 3. 100 м. 6*. Сторона искомого квадрата равна диагонали данного квадрата.

58

В а р и а н т  1. 1. 66 см². 2. 12 см. 3. 81 дм². 4. 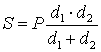. 5*. Параллелограммы. 6*. 216 см².

В а р и а н т  2. 1.  см². 2. 30°, 30°, 150°, 150°. 3. 32 дм. 4. 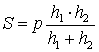. 6*. 4Q.

59

В а р и а н т  1. 1. 3 дм². 2. . 3. а) Нет; б), в) да. 4. Две прямые, параллельные прямой AB, отстоящие от нее на расстояние h. 5*. Решение представлено на рисунке 31. 6*.  см².

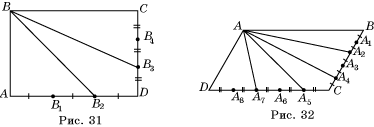
В а р и а н т  2. 1.  см. 2. . 3. а), б) Да; в) нет. 5*. Решение представлено на рисунке 32. 6*.  см².

60

В а р и а н т  1. 1. 8,5 см. 3. 20 см². 5*. . 6*. .

В а р и а н т  2. 1. 4 см. 3. 19,5 см². 5*. 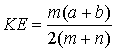. 6*. .

61

В а р и а н т  1. 1. 2R². 2. 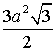. 3. 48 см. 4. 38,25 см². 5*. . 6*. Решение представлено на рисунке 33.

В а р и а н т  2. 1. 4r². 2. . 3. 20. 4. 182,25. 5*. . 6*. Решение представлено на рисунке 34.

62

В а р и а н т  1. 1. 34 см; 34 см. 2. 423p мм². 3. 100 см². 4. .

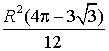В а р и а н т  2. 1. 38 см; 361 см². 2. 63p мм². 3. 40 дм. 4. .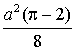

63

В а р и а н т  1. 1. 9 см². 2. 1 : 36. 3. 7 дм², 63 дм², 343 дм². 4. . 5*. Решение представлено на рисунке 35. 6*. , .

В а р и а н т  2. 1. 16 см². 2. 3 : 1. 3. 200 дм². 4. 80 см² и 120 см². 5*. Решение представлено на рисунке 35. 6*. .

64

В а р и а н т  1. 1. а) CD; б) BD; в) нельзя определить. 2. 851 см². 3. Равнобедренный треугольник (воспользуйтесь рисунком 36). 4. Равнобедренный треугольник (воспользуйтесь рисунком 37). 6*. Воспользуйтесь рисунком 38.

В а р и а н т  2. 1. Наименьшая – DE; наибольшая – DF. 2. 0 < S < 246,5 см². 3. Квадрат (воспользуйтесь рисунком 39). 4. Воспользуйтесь рисунком 40. 5*. Воспользуйтесь рисунком 41. 6*. Воспользуйтесь рисунком 42.

65

В а р и а н т  1. 1. Разрезать по медиане. 2. Разрезать по медианам. 3. Решение показано на рисунке 43. 4. Решение показано на рисунке 44. 5*. Решение показано на рисунке 45.

В а р и а н т  2. 1. Разрезать по прямым, проходящим через вершину треугольника и делящим противоположную сторону на три равные части. 3. Решение показано на рисунке 46. 4. Решение показано на рисунке 47. 5*. Решение показано на рисунке 48.

66

В а р и а н т  1. 1. H(1, 0), P(0, 0). 2. а) (5,5, -6); б) (-5, -3,5). 3. (4, 0). 4. а) (4, -9); б) (4, 9); в) (-4, -9). 5*. Точки вне полосы, ограниченной прямыми x = 5, x = -5. 6*. Точки вне круга с центром в начале координат и радиусом .

В а р и а н т  2. 1. E(0, 1), F(3, 0). 2. а) (3, -5,5); б) (0,4, -2). 3. (0, -3). 4. а) (6, 4); б) (-6, -4); в) (-6, 4). 5*. Точки полосы, ограниченной прямыми y = 4, y = -4. 6*. Внутренние точки круга с центром в начале координат и радиусом .

67

В а р и а н т  1. 1. . 2. x² + (y + 13)² = 121. 3. Равнобедренный, . 4. (0, -1). 5*. Да. 6*. (-6, 6), (-30, 30).

В а р и а н т  2. 1. . 2. (x + 11)² + y² = 144. 3. Равнобедренный, . 4. 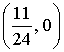. 5*. Нет. 6*. (-4, 4), (20, -20).

68

В а р и а н т  1. 3. а) ; б) .

В а р и а н т  2. 3. а) ; б) .

69

В а р и а н т  1. 3. а) ; б) ; в) ; г) . 4. а) m > 0; б) 0 < m < 1. 5*. , где 0 < a < 1. 6*. Указание. Если M не принадлежит KL, то в треугольнике MKL продолжите медиану MO на равный ей отрезок OM₁ и рассмотримте параллелограмм KMLM₁.

В а р и а н т  2. 3. а) ; б) ; в) ; г) . 4. а) n < 0; б) k > 1, k < -1. 5. , где a < 0 и , где b < 0.

70

В а р и а н т  1. 2. а) (1, -1); б) (5, -1); в) (-10, -6); г) (20, -13). 3. а) (-14, -4); б) (8, -2). 4. (9,6, -6,4).

Вариант 2. 2. а) (0, -2); б) (-15, 11); в) (24, 20); г) (12, 9). 3. а) (37, -48); б) (-10, 1). 4. (-6,4, 12).

71

В а р и а н т  1. 1. . 2. а) 8; б) -12; в) 0. 3. Тупоугольный. 4. . 5*. 57.

В а р и а н т  2. 1. 2. 2. а) 1; б) ; в) 0. 3. Тупоугольный. 4. -6. 5*. 66.

72

В а р и а н т  1. 1. x + 5 = 0. 2. (0, 4), (-2, 0). 3. x – y – 3 = 0, (1, -1). 4. (7, -3). 5*. 2x + 3y + 16 = 0, 3x – 2y + 11 = 0. 6*. y – 5 = 0.

В а р и а н т  2. 1. y +4 = 0. 2. (0, 2), (12, 0). 3. 3x + 2y = 0, (3, 2). 4. (-3, 4). 5*. а) (x + 1)² + (y – 3)² = 9; б) (x + 0,5)² + (y – 6)² = 0,25. 6*. x – 13 = 0.

73

В а р и а н т  1. 1. Первая и четвертая четверти координатной плоскости. 2. Квадрат, расположенный во второй четверти координатной плоскости. 5*. (1, 2), y + 6 = 0. 6*. .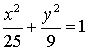

В а р и а н т  2. 1. Третья и четвертая четверти координатной плоскости. 2. Прямоугольник, расположенный в четвертой четверти координатной плоскости. 5*. (0, -2), . 6*. F₁(-, 2), F₂(, 2), (, 0), (-, 0).

74*

В а р и а н т  1. 5*. 10,5. 6*. Да.

В а р и а н т  2. 5*. 20. 6*. Да.

75

В а р и а н т  1. 3. а) -2; б) 2,5; в) 0; г) . 4. а) 0; б) 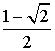; в) -3; г) . 5*. а) a = 90° + 360°n, где n – произвольное целое число; б) b = 180°n, где n – произвольное целое число. 6*. а) -90° + 360°n £ g £ 90° + 360°n, где n – произвольное целое число; б) -30° + 180°n < g < 30° + 180°n, где n – произвольное целое число.

В а р и а н т  2. 3. а) 0; б) 0; в) 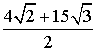; г) . 4. а) 0; б) ; в) ; г) -1. 5*. b= -180° + 360°n, где n – произвольное целое число; б) a = 90°+ 180°n, где n – произвольное целое число. 6*. а) 360°n <  < 180° + 360°n, где n – произвольное целое число; б) -45° + 180°n £  £ 45 + 180°n, где n – произвольное целое число.

76

В а р и а н т  1. 2. а) (-1, 0); б) (0, -2). 3. а) Окружность с центром в начале координат и радиусом 1; б) луч с вершиной в начале координат, составляющий с полярной осью угол . 4. rcos j= -2. 5*. . 6*. .

В а р и а н т  2. 2. а) (, ); б) (2, ), б) Да. 3. а) Луч с вершиной в начале координат, составляющий с полярной осью угол 30°; б) Окружность с центром в начале координат и радиусом 2. 4. rsin j= -1. 5*. . 6*. .