§ 5. ЗАДАЧИ С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ
Площадь многоугольников
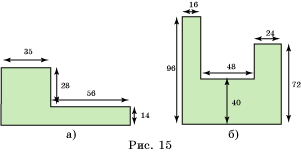
1. Найдите площадь участка, план которого приведен на рисунке 15. (Размеры даны в метрах.) Выразите площадь в: а) арах; б) гектарах.
2. Площадь земельного участка, имеющего форму прямоугольника, равна 9 га, ширина равна 150 м. Найдите длину этого участка.
3. Пол в танцевальном зале имеет форму прямоугольника размером 8 м x 15 м. Его требуется покрыть паркетной плиткой. Сколько нужно подготовить квадратных плиток, размером 50 см x 50 см, если на обрезки и пригонку затрачивается 2% площади всех плиток.
4. Вычислите давление, которое оказывает прибор весом 7,65 т на на 1 см2 своего фундамента, имеющего форму равностороннего треугольника со стороной 3 м.
5.
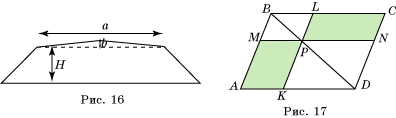
На рисунке 16 изображен поперечный профиль дороги. Вычислите его площадь, если
ширина полотна дороги a = 7,5 м, h – стрела
подъема полотна над насыпью составляет 2% ширины полотна, откосы наклонены к
линии горизонта под углом 45![]() и высота насыпи H = 1,5 м.
и высота насыпи H = 1,5 м.
6. Земельный участок треугольной формы, назовем его MNK, площади 5 га нужно разделить межой MX на две части так, чтобы площадь MXK составила 1,5 га. Найдите длину KX, если KN = 40 м.
7. Земельный участок имеет форму треугольника. Как разделить его на три равновеликих участка таким образом, чтобы в каждом было по одной стороне треугольника?
8. Найдите наиболее простой способ деления поля, имеющего форму параллелограмма на: а) две; б) четыре равновеликие части прямыми, выходящими из одной вершины.
9. Как через точку внутри квадратной поляны провести прямую тропинку так, чтобы она отсекла участок наименьшей площади.
10. На куске фанеры, имеющей форму параллелограмма сделали разметку, как показано на рисунке 17, где KL || AB и MN || BC, и выпилили четырехугольники AMPK и PLCN. Равновелики ли эти четырехугольники? Зависит ли равновеликость от выбора точки P на диагонали BD?
11. Найдите площадь поперечного сечения ромбовидных напильников, диагонали которых равны: а) 1,3 см и 36 мм; б) 2,1 мм и 2,7 см.
12.
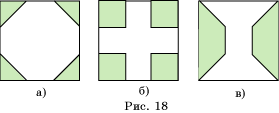
Какие измерения нужно произвести, чтобы найти площадь вырезанной из квадратного
листа фанеры рамки, имеющей форму: а) восьмиугольника (рис. 18, а); б)
греческого креста (рис. 18, б); в) восьмиугольника (рис. 18, в). (Каждая
сторона квадрата разделена на три равные части.) Найдите площадь рамки, если
взят единичный квадрат.
13. Детская площадка квадратной формы огорожена забором, закрепленном с помощью четырех столбов, находящихся в вершинах квадрата. Как увеличить площадь в два раза, чтобы новая площадка тоже имела форму квадрата, и столбы остались по ее периметру.
14.
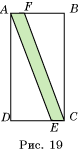
Из листа цветной бумаги прямоугольной формы (рис. 19, AE || CF) вырезали два
треугольника. Найдите процент оставшейся от листа площади, если DC = 20 см, AF =
2,2 см.
15. Из листа фанеры прямоугольной формы размером 220 см x 160 см необходимо вырезать заготовки в виде равнобедренных трапеций с основаниями 20 см, 60 см и углом 45°. Сколько заготовок получится из данной фанеры? Определите процент неизрасходованной площади.
16. Найдите площадь клумбы, имеющей форму трапеции, если одна из ее боковых сторон равна 8 м, угол 30° и известно, что вокруг нее можно описать окружность и в нее можно вписать окружность.
17. Пол кухни размера 3 м x 3 м нужно застелить линолиумом, состоящим из плиток формы: а) правильных восьмиугольников и квадратов; б) правильных шестиугольников. Сколько потребуется плиток, если их стороны равны 15 см?
18. Как разделить участок, имеющий форму выпуклого четырехугольника на две равновеликие части межой, проведенной через одну из его вершин?
19. Сколько потребуется краски, чтобы выкрасить с двух сторон железный щит в виде прямоугольного треугольника, если гипотенуза треугольника равна 5 м, разность катетов равна 3 м и на 5 см2 расходуется 1,8 г краски.
20. Внутри участка, имеющего форму правильного шестиугольника, решили посадить цветы в виде клумбы, также имеющей форму шестиугольника и образованной меньшими диагоналями внешнего шестиугольника. Найдите площадь клумбы, если площадь участка равна 8,4 м2.
Площадь круга и его частей
21. Дерево имеет в обхвате 1,2 м. Найдите площадь поперечного сечения в этом месте, имеющего приблизительно форму круга.
22. Часы, установленные на высотном здании Московского государственного университета имеют диаметр около 8,8 м. Найдите площадь, которую занимает циферблат этих часов. Сравните ее с площадью вашего кабинета.
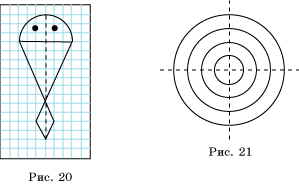
23.
Найдите площадь бумажного змея, чертеж которого приведен на рисунке 20 в
масштабе 1 клетка = 0,1 м.
24. Из медного квадратного листа вырезали круг наибольшего диаметра. Найдите площадь листа, если площадь круга равна 68,68 см2.
25. Сколько нужно семян, чтобы засеять круглую клумбу диаметром 3,2 м, если на 1 см2 идет 0,0004 г?
26. Сколько нужно песка, чтобы окружить круглую клумбу прилегающей к ней дорожкой шириной 0,5 м, если на 1 м2 требуется 0,8 дм3 песка и наибольший диаметр равен 18 м?
27. В будильнике минутная стрелка длиннее часовой на 8 мм. Найдите длину этих стрелок, если площадь кольца, заключенного между окружностями, которые они описывают, равна 13,5 см2.
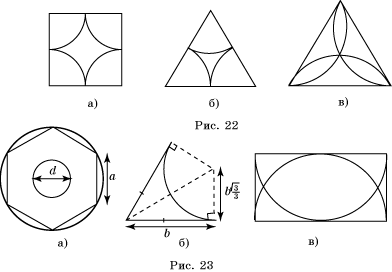
28. На рисунке 21 изображена мишень. В каком отношении находятся площади ее наименьшего круга и круговых колец, если ширина каждого кольца равна радиусу внутреннего круга.
29. Найдите площади сечений деталей, заштрихованных на рисунке 22, приняв стороны равностороннего треугольника и квадрата за единицу. В случае в) сторона квадрата разделена на три равные части, в случае д) в отношении 1 : 2 : 1.
30. Найдите площади деталей, заштрихованных на рисунке 23.
Координаты и векторы
31.
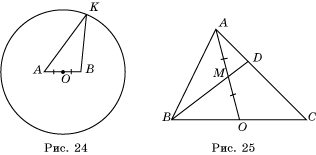
На рисунке 24 изображено колесо карусели, закрепленное в центре O планкой AB, причем AO = OB. По периметру колеса расположены
кресла. Докажите, что сумма квадратов расстояний от них до концов планки есть
величина постоянная.
32. Проводятся соревнования по ориентированию на местности. Участникам раздали карты, на которых пункты сбора отмечены в вершинах четырехугольника, имеющих координаты A(-2, -5), B(-5, 3), C(3, 9), D(8, -3). Спортсмены разбиты на четыре команды, которые должны начать движение из точек E, F, G и H – середин соответствующих сторон AB, BC, CD и AD четырехугольника – в пункты, расположенные в серединах отрезков, соединяющих середины противоположных сторон четырехугольника. Изобразите план и определите координаты точек E, F, G, H, точек – пунктов встреч, а также расстояние, которые прошли команды до места встреч.
33. Определите расстояние между пунктом O и недоступной точкой M, если известны расстояния ( в км) OA, OB и OC, где A, B, C – пункты, расположенные в вершинах треугольника, центроидом которого является точка M. Точки имеют следующие координаты: O(0, 0), A(-7, 8), B(8, 15), C(-4, 1).
34.
Участок ABC треугольной формы разделили на
две равновеликие части, проведя межу AO (рис. 25). В свою очередь AO тоже разделили пополам вехой M и провели
межу BM, которая пересекла AC в точке D. Докажите, что ![]() .
.
35. К одной точке приложены три силы P1 = 30H, P2 = 50H, P3 = 30H, располагающиеся в одной плоскости. Углы между соседними силами равны 120°. Найдите величину и направление равнодействующей силы.
36. Какую силу нужно приложить к прямолинейному направлению движения под углом: а) 45°; б) 60°, чтобы на пути в 1 км она совершила работу, равную 200 Дж?
37. Под каким углом нужно приложить силу в 20 H к прямолинейному направлению движения, чтобы на пути в 50 м она совершила работу в 100 Дж?
38.
Какой угол образуют единичные векторы ![]() и
и ![]() , если известно, что векторы
, если известно, что векторы ![]() + 2
+ 2![]() и 5
и 5![]() - 4
- 4![]() перпендикулярны.
перпендикулярны.
39.
Какой геометрический смысл имеет формула: а) (![]() +
+ ![]() )(
)(![]() –
– ![]() ) =
) = ![]() 2 +
2 + ![]() 2; б) (
2; б) (![]() +
+ ![]() )2 + (
)2 + (![]() –
– ![]() )2 = 2(
)2 = 2(![]() 2 +
2 + ![]() 2)?
2)?
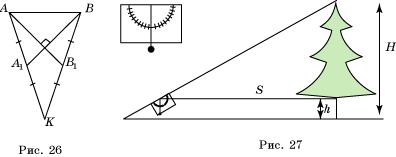
40. Под каким углом видит путешественник береговую полосу AB с корабля K, если KAB – равнобедренный треугольник, медианы которого, проведенные к боковым сторонам перпендикулярны (рис. 26).
Тригонометрия
41. Тропинка длиной 1,8 км, поднимаясь в гору, образует с горизонтом угол 6°. На какой высоте от подошвы горы находится база альпинистов, расположенная на вершине горы.
42. Объясните, как можно найти высоту дерева, используя прибор – высотомер, изображенный на рисунке 27.
43. Самолет был обнаружен вертикальным лучом прожектора, расположенным в 1,5 км от аэропорта. В то же время диспетчер в аэропорту увидел этот самолет под углом в 30°. Найдите высоту, на которой находился самолет в этот момент и расстояние от самолета до аэропорта.
44. Самолет находится на высоте 7000 м и приближается к аэропорту. Для посадки летчик должен производить снижение под постоянным углом 6°. На каком расстоянии от посадочной полосы он должен начать снижение?
45. Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши равна 5 м. Под каким углом к потолку поставлены стропила крыши?
46. На склоне холма стали рыть туннель длиной 0,5 км по направлению, составляющему с горизонтом угол 5°. На каком расстоянии от поверхности холма будет находиться конец туннеля, если скат холма образует с горизонтом угол наклона 30°?
47. Для определения высоты колонны поступили следующим образом: отошли от ее основания на 100 м, поставили угломерный прибор высотой 1,6 м и установили, что вершина колонны видна под углом 22°. Найдите высоту колонны.
48. Из некоторой точки вершина горы видна под углом 30°. При приближении к горе на 0,5 км вершина стала видна под углом 45°. Найдите высоту горы.
49. Корабль движется на восток со скоростью 16 узлов (один узел равен одной морской миле в час, одна морская миля равна 1,852 км). В 12 часов азимут направления на маяк составил 60°, а в 12 часов 30 минут составил 30°. Определите расстояние, на котором находился корабль от маяка в 12 часов 30 минут.
50. Из городов A и C одновременно выезжают два поезда в направлениях AB и CD. Скорость первого поезда 80 км/ч, второго – 100 км/ч. Направления движения AB и CD пересекаются в точке M под углом 60°, причем AM = 150 км, CM = 120 км. Определите, через какое время от начала движения поезда удалятся друг от друга на расстояние, равное расстоянию между городами A и C.
ОТВЕТЫ
1. а) 22,54 а; б) 0,5184 га. 2. 600 м. 3. 490 плиток. 4. ![]() 0,2 кг/см2. 5.
14,0625 м2. 6. 12 м. 7. Найти точку пересечения медиан и
соединить ее с вершинами треугольника. 8.
а) Провести диагональ параллелограмма; б) провести диагональ, затем в
образовавшихся треугольниках – медианы. 9.
Если точка – центр квадрата, то решений бесконечно много – это любая прямая,
проходящая через центр. В других случаях нужно провести прямую,
перпендикулярную диагонали. 10.
Данные четырехугольники – равновеликие параллелограммы. 11. а) 2,34 см2; б) 0,2835 см2. 12. а)
0,2 кг/см2. 5.
14,0625 м2. 6. 12 м. 7. Найти точку пересечения медиан и
соединить ее с вершинами треугольника. 8.
а) Провести диагональ параллелограмма; б) провести диагональ, затем в
образовавшихся треугольниках – медианы. 9.
Если точка – центр квадрата, то решений бесконечно много – это любая прямая,
проходящая через центр. В других случаях нужно провести прямую,
перпендикулярную диагонали. 10.
Данные четырехугольники – равновеликие параллелограммы. 11. а) 2,34 см2; б) 0,2835 см2. 12. а) ![]() ; б), в)
; б), в) ![]() . 13. Решение
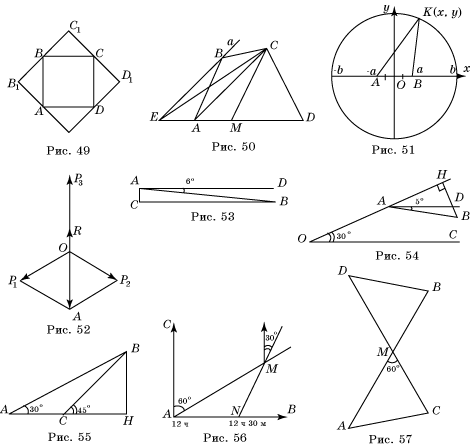
показано на рисунке 49. 14. 11%. 15. 42, »4,5%. 16. 32 м2. 17.
а) »200
плиток; б) »154
плитки. 18. Решение показано на
рисунке 50. 19. 28,8 кг. 20. 2,8 м2. 21. »0,12 м. 22. »61 м2. 23. »0,52 м2. 24. 88 см2. 25. »32 г. 26. »22
дм3. 27. 3,2 см, 2,4 см. 28. 1 : 3 : 5 : 7. 29. а)
. 13. Решение
показано на рисунке 49. 14. 11%. 15. 42, »4,5%. 16. 32 м2. 17.
а) »200
плиток; б) »154
плитки. 18. Решение показано на
рисунке 50. 19. 28,8 кг. 20. 2,8 м2. 21. »0,12 м. 22. »61 м2. 23. »0,52 м2. 24. 88 см2. 25. »32 г. 26. »22
дм3. 27. 3,2 см, 2,4 см. 28. 1 : 3 : 5 : 7. 29. а) ![]() ; б)
; б) 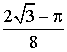 ; в)
; в) 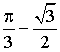 . 30. а)
. 30. а) 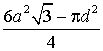 ; б)
; б) 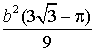 ; в)
; в) 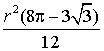 . 31. Решение
показано на рисунке 51. 32. E(-3,5,
-1), F(-1, 6), G(5,5, 3), H(3, -4). Середины
EG и FH
совпадают, это точка с координатами (1, 1). 33.
. 31. Решение
показано на рисунке 51. 32. E(-3,5,
-1), F(-1, 6), G(5,5, 3), H(3, -4). Середины
EG и FH
совпадают, это точка с координатами (1, 1). 33. ![]() »
8,065 (км). 35. Решение показано на
рисунке 52; равнодействующая сила R = 20H. 36. а) »0,39H; б) »0,23H. 37. a»71
»
8,065 (км). 35. Решение показано на
рисунке 52; равнодействующая сила R = 20H. 36. а) »0,39H; б) »0,23H. 37. a»71![]() 36’. 38. 60
36’. 38. 60![]() . 40.
. 40. ![]() »36
»36![]() 52’. 41. 188 м. 43. 866 м; 1,733 км. 44. Решение показано на рисунке 53; BC » 67 км. 45. »53
52’. 41. 188 м. 43. 866 м; 1,733 км. 44. Решение показано на рисунке 53; BC » 67 км. 45. »53![]() . 46. Решение показано
на рисунке 54; HB » 287
м. 47. 42 м. 48. Решение показано на рисунке 55; BH »
683 м. 49. Решение показано на
рисунке 56; NM »14,816
км. 50. Решение показано на рисунке
57; t » 2 ч 48 мин.
. 46. Решение показано
на рисунке 54; HB » 287
м. 47. 42 м. 48. Решение показано на рисунке 55; BH »
683 м. 49. Решение показано на
рисунке 56; NM »14,816
км. 50. Решение показано на рисунке
57; t » 2 ч 48 мин.