§ 4. Т Е С Т Ы

 

Тест № 1 «Параллельность»

1. Сколько  углов образуется при пересечении двух параллельных прямых третьей?

1) 4.

2) 6.

3) 8.

4) 12.

2. Сколько равных острых углов может образоваться при пересечении двух параллельных прямых третьей?

1) 2.

2) 4.

3) 6.

4) 8.

3. Сколько равных тупых углов может образоваться при пересечении двух параллельных прямых третьей?

         1) 2.

         2) 4.

         3) 8

         4) 16.

4. Сколько прямых углов может образоваться при пересечении двух параллельных прямых третьей?

         1) 0

         2) 2.

         3) 4.

         4) 8.

5. При пересечении двух параллельных прямых третьей один из углов оказался равным 34°. Найдите наименьший из всех образованных при этом углов.

         1) Нельзя определить.

         2) 34°.

         3) 68°.

         4) 146°.

6. При пересечении двух параллельных прямых третьей один из углов оказался равным 112°. Найдите наименьший из всех образованных при этом углов.

         1) Нельзя определить.

         2) 34°.

         3) 68°.

         4) 112°.

7. При пересечении двух параллельных прямых третьей внешние накрест лежащие углы оказались равными 65°. Найдите внутренние накрест лежащие углы.

1) 65° и 115°.

         2) 125°.

         3) 65°.

         4) 65° и 180°.

8. При пересечении двух параллельных прямых третьей один из углов оказался равным 97°. Найдите наименьший из всех образованных при этом углов.

1) 97°.

         2) 83°.

         3) 77°.

         4) 7°.

9. Сумма трех внутренних углов, образовавшихся при пересечении двух параллельных прямых третьей, равна 290°. Найдите четвертый внутренний угол.

         1) 145°.

         2) 110°.

         3) 35°.

         4) 70°.

10. При каком положении секущей ее отрезок, заключенный между параллельными прямыми, имеет наименьшую длину?

         1) Нельзя определить.

2) Секущая параллельна данным прямым.

         3)  Секущая перпендикулярна данным прямым.

         4) Секущая пересекает данные прямые под углом 45°.

11. Как расположены относительно друг друга биссектрисы внутренних односторонних углов, которые получились при пересечении двух параллельных прямых третьей?

         1) Нельзя определить.

2) Параллельны.

         3) Перпендикулярны.

         4) Пересекаются под углом 45°.

12. Как расположены относительно друг друга биссектрисы внешних накрест лежащих углов, которые получились при пересечении двух параллельных прямых третьей?

         1) Нельзя определить.

2) Параллельны.

         3) Перпендикулярны.

         4) Пересекаются под углом 45°.

13. Найдите углы треугольника, которые относятся как 2:3:4.

         1) 20°, 30°, 40°.

2) 40°, 60°, 80°.

         3) 36°, 54°, 90°.

         4) 18°, 27°, 36°.

14. Определите вид треугольника, если его углы относятся как 1:2:3?

         1) Нельзя определить.

         2) Остроугольный.

         3) Прямоугольный.

         4) Тупоугольный.

15. Определите вид треугольника, если один из его углов больше суммы двух других?

         1) Нельзя определить.

         2) Остроугольный.

         3) Прямоугольный.

         4) Тупоугольный.

16. Угол при основании равнобедренного треугольника равен 70°. Найдите угол между его высотой, проведенной к боковой стороне, и другой боковой стороной.

         1) 20°.

2) 50°.

         3) 70°.

         4) 110°.

17. Определите вид треугольника, если у него один внешний угол острый.

         1) Нельзя определить.

         2) Остроугольный.

         3) Прямоугольный.

         4) Тупоугольный.

18. Найдите сумму углов выпуклого семиугольника.

1) 180°.

2) 630°.

         3) 900°.

         4) 1260°.

19. Найдите угол правильного восьмиугольника.

1) 45°.

2) 135°.

         3) 720°.

         4) 1080°.

20. Сумма углов выпуклого n-угольника равна 1260°. Найдите n.

1) 8.

2) 9.

         3) 10.

         4) 12.

 

Тест № 2 «Четырехугольники»

1. Сколько разных параллелограммов можно получить из двух равных разносторонних треугольников, прикладывая их друг к другу различным образом?

         1) 1.

2) 2.

         3) 3.

         4) 6.

2. Сумма двух углов параллелограмма равна 126°. Найдите его углы.

         1) 63°, 63°, 126°, 126°.

2) 54°, 126°, 54°, 126°.

         3) 63°, 117°, 63°, 117°.

         4) 54°, 126°, 63°, 117°.

3. Диагональ параллелограмма образует с двумя его сторонами углы 24° и 46°. Найдите углы параллелограмма.

         1) 24°, 156°, 46°, 134°.

2) 22°, 68°, 22°, 68°.

         3) 70°, 70°, 110°, 110°.

         4) 22°, 158°, 22°, 158°.

4. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2:3, считая от вершины тупого угла. Найдите несмежные стороны параллелограмма, если его периметр равен 90 см.

         1) 16,875 см, 28,125 см.

2) 18 см, 27 см.

         3) 32 см, 58 см.

         4) 45 см, 135 см.

5. В прямоугольнике перпендикуляры, проведенные из точки пересечения диагоналей к его сторонам равны соответственно 3 см и 5 см. Найдите периметр прямоугольника.

         1) 16 см.

2) 24 см.

         3) 32 см.

         4) 48 см.

6. В треугольнике ABC C=90°, AC=BC=12 см. Из точки M, взятой на AB, проведены прямые, параллельные катетам. Найдите периметр образовавшегося четырехугольника.

         1) 12 см.

2) 24 см.

         3) 30 см.

         4) 48 см.

7. Определите вид четырехугольника, вершины которого находятся в серединах сторон прямоугольника.

         1) Параллелограмм общего вида.

2) Прямоугольник.

         3) Ромб.

         4) Квадрат.

8. В ромбе одна из диагоналей равна его стороне. Найдите углы ромба.

1) 30°, 60°, 30°, 60°.

2) 30°, 150°, 30°, 150°.

         3) 60°, 60°, 120°, 120°.

         4) 45°, 45°, 135°, 135°.

9. В ромбе перпендикуляр, проведенный из вершины тупого угла, делит сторону пополам. Найдите углы ромба.

1) 60°, 60°, 120°, 120°.

2) 45°, 45°, 135°, 135°.

         3) 90°, 90°, 90°, 90°.

         4) 30°, 30°, 150°, 150°.

10. Из точки пересечения диагоналей ромба опущены на его стороны перпендикуляры, основания которых последовательно соединены отрезками. Определите вид образовавшегося четырехугольника.

         1) Параллелограмм общего вида.

2) Прямоугольник.

         3) Ромб.

         4) Квадрат.

11. Из каких двух равных треугольников можно сложить квадрат?

         1) Правильных.

2) Прямоугольных.

3) Равнобедренных.

         4) Равнобедренных прямоугольных.

12. В параллелограмме одна из диагоналей делит его угол пополам. Определите его вид.

         1) Параллелограмм общего вида.

2) Прямоугольник.

         3) Ромб.

         4) Квадрат.

13. В четырехугольнике диагонали равны, перпендикулярны и в точке пересечения делятся пополам. Определите вид четырехугольника.

         1) Параллелограмм общего вида.

2) Прямоугольник.

         3) Ромб.

         4) Квадрат.

14. В равнобедренный прямоугольный треугольник вписан квадрат (вершины принадлежат сторонам треугольника), имеющий с ним общий угол. Найдите периметр квадрата, если катет треугольника равен b.

         1) .

2) 2b.

         3) 4b.

         4) b².

15. Стороны треугольника относятся как 1:3:4, его периметр равен 48 см. Найдите стороны треугольника, вершины которого находятся в серединных сторон данного треугольника.

         1) 6 см, 18 см, 24 см.

2) 3 см, 9 см, 12 см.

         3) 12 см, 36 см, 24 см.

         4) 8 см, 24 см, 32 см.

16. В равностороннем треугольнике со стороной, равной 18 см, через середину одной из них проведены прямые, параллельные двум другим сторонам. Найдите периметр образовавшегося четырехугольника.

         1) 18 см.

2) 36 см.

         3) 48 см.

         4) 72 см.

17. Углы при основании трапеции равны 71° и 34°. Найдите остальные ее углы.

         1) 34°, 71°.

2) 56°, 19°.

         3) 105°, 75°.

         4) 109°, 146°.

18. В равнобедренной трапеции основания равны 13 см и 28 см., острый угол равен 60°. Найдите ее периметр.

         1) 41 см.

2) 71см.

         3) 82 см.

         4) 20,5 см.

19. В прямоугольной трапеции один из углов равен 45°, средняя линия равна 24 см, основания относятся как 3:5. Найдите меньшую боковую сторону.

         1) 12 см.

2) 6 см.

         3) 24 см.

         4) 32 см.

20. Средняя линия трапеции делится ее диагоналями на части, которые относятся как 2:3:2. Найдите основания трапеции, если ее средняя линия равна 42 см.

         1) 12 см, 30 см.

2) 24 см, 30 см.

         3) 24 см, 60 см.

         4) 24 см, 36 см.

 

Тест № 3 «Вписанные и описанные многоугольники»

1. Где находится центр окружности, описанной около треугольника?

         1) В ортоцентре (точка пересечения прямых, на которых лежат высоты треугольника).

         2) В центроиде (точка пересечения медиан треугольника).

         3) В точке пересечения серединных перпендикуляров сторон.

         4) В точке пересечения биссектрис.

2. Где находится центр окружности, вписанной в треугольник?

         1) В ортоцентре.

         2) В центроиде.

         3) В точке пересечения серединных перпендикуляров сторон.

         4) В точке пересечения биссектрис.

3. Определите вид треугольника, если центр описанной около него окружности находится на одной из его сторон.

         1) Равносторонний.

         2) Остроугольный.

         3) Прямоугольный.

         4) Тупоугольный.

4. Какой вид имеет треугольник, если расстояние от его ортоцентра до центра описанной около него окружности больше радиуса этой окружности?

1) Равносторонний.

         2) Остроугольный.

         3) Прямоугольный.

         4) Тупоугольный.

5. Какой вид имеет треугольник, если расстояние от его ортоцентра до центра описанной около него окружности равно радиусу этой окружности?

1) Равносторонний.

         2) Остроугольный.

         3) Прямоугольный.

         4) Тупоугольный.

6. Центр окружности, вписанной в треугольник, лежит внутри него. Определите вид треугольника.

         1) Остроугольный.

         2) Прямоугольный.

         3) Тупоугольный.

         4) Нельзя определить.

7. Во сколько раз радиус окружности, описанной около равностороннего треугольника, больше радиуса вписанной в этот треугольник окружности?

         1) В 2 раза.

         2) В 3 раза.

         3) В 4 раза.

         4) В 6 раз.

8. Центральный угол окружности на 42° больше вписанного угла, опирающегося на ту же дугу. Найдите эти углы.

         1) 42°, 84°.

2) 42°, 21°.

3) 14°, 28°.

4) 21°, 10°30’.

9. В окружности проведена хорда, равная радиусу. Под каким углом видна эта хорда из произвольной точки окружности, отличной от ее концов?

         1) 30°.

2) 60°.

3) 90°.

4) 180°.

10. Под каким углом из точки дуги видна стягивающая ее хорда, если дуга составляет 20% окружности?      

1) 36°.

2) 72°.

3) 144°.

4) 288°.

11. В угол вписана окружность. Точки касания делят ее на две части, которые относятся как 7:11. Найдите данный угол.

1) 40°.

2) 70°.

3) 110°.

4) 140°.

12. Около четырехугольника ABCD описана окружность. Его углы A, B, C относятся как 1:2:3. Найдите угол D. 

1) 30°.

2) 45°.

3) 60°.

4) 90°.

13. В четырехугольник ABCD вписана окружность, AB=11 см, CD=17 см. Найдите периметр четырехугольника.      

1) 14 см.

2) 28 см.

3) 40 см.

4) 56 см.

14. Меньшая сторона прямоугольника равна 3,6 см. Угол между диагоналями 120°. Найдите диаметр описанной окружности.

1) 1,8 см.

2) 3,6 см.

3) 7,2 см.

4) 14,4 см.

15. Найдите радиус окружности, вписанной в ромб со стороной 12 см и углом 30°.

         1) 3 см.

         2) 4 см.

         3) 6 см.

         4) 8 см.

16. Периметр прямоугольной трапеции, описанной около окружности, равен 20 см, ее большая боковая сторона равна 6 см. Найдите радиус окружности.

         1) 2 см.

         2) 4 см.

         3) 10 см.

         4) 14 см.

17. Какой наибольший центральный угол может быть у правильного многоугольника, вписанного в окружность?

         1) 60.

         2) 90.

         3) 120.

         4) Нельзя определить.

18. Периметр правильного шестиугольника, вписанного в окружность, равен 36 см. Найдите диаметр окружности.

         1) 6 см.

         2) 9 см.

         3) 12 см.

         4) 18 см.

19. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из  вершин стороны, равен 70°. Найдите n.

         1) 6.

         2) 8.

         3) 9.

         4) 12.

20. Найдите число сторон правильного многоугольника, у которого угол на 108° больше центрального угла описанной окружности.

         1) 5.

         2) 10.

         3) 12.

         4) 15.

 

Тест № 4 «Движение»

1. Какие прямые при центральной симметрии переходят в себя?

         1) Параллельные.

         2) Перпендикулярные.

         3) Проходящие через центр симметрии.

         4) Таких прямых нет.

2. Как расположены относительно друг друга две центрально симметричные прямые?

         1) Совпадают.

2) Параллельны или совпадают.

         3) Перпендикулярны.

         4) Пересекаются в центре симметрии.

3. При каком расположении трех различных прямых образованная ими фигура имеет бесконечно много центров симметрии?

         1) Прямые параллельны.

         2) Прямые пересекаются в одной точке.

         3) Две прямые параллельны, третья им перпендикулярна.

         4) Прямые параллельны и одна из них находится на равных расстояниях от двух других.

4. Какому условию должны удовлетворять два луча, чтобы они были центрально симметричными?

         1) Лежать в одной полуплоскости относительно прямой, проходящей через их начала.

         2)  Лежать на параллельных прямых.

         3) Быть сонаправленными.

         4) Быть противоположно направленными.

5. Какие точки переходят в себя при повороте вокруг некоторой точки на угол j?

         1) Принадлежащие прямым, проходящим через центр поворота.

         2) Принадлежащие углам с вершиной в центре поворота.

         3) Центр поворота.

         4) Лучи с началом в центре поворота.

6. На какой угол нужно повернуть прямую вокруг точки, не принадлежащей ей, чтобы получить прямую, параллельную данной?

1)  90°.

2) 180°.

3) 270°.

4) 360°.

7. Поворот на какой положительный угол совпадает с поворотом на угол –j (0°<j<360°)?

         1) 360°-j.

         2) 180°-j.

         3) 180°+j.

         4) 90°+j.

8. Центром симметрии какого порядка является точка пересечения диагоналей произвольного параллелограмма?

         1) Второго.

         2) Третьего.

         3) Четвертого.

         4) Шестого.

9. Какие прямые при осевой симметрии переходят в себя?

         1) Параллельные оси.

         2) Перпендикулярные оси.

         3) Ось и перпендикулярные ей прямые.

4) Пересекающие ось под углом 45°.

10. При каком условии прямая при осевой симметрии переходит в параллельную себе прямую?

         1) Совпадает с осью.

         2) Параллельна оси.

         3) Перпендикулярна оси.

         4) Таких прямых нет.

11. Сколько осей симметрии имеет правильный пятиугольник?

         1) 0.

         2) 5.

         3) 10.

         4) 20.

12. Сколько осей симметрии имеет правильный шестиугольник?

         1) 3.

         2) 6.

         3) 9.

         4) 12.

13. Сколько существует параллельных переносов, переводящих луч в сонаправленный ему луч?

         1) 1.

         2) 2.

         3) 3.

         4) Бесконечно много.

14. При каком условии существует параллельный перенос, переводящий один отрезок в другой?

         1) Отрезки равны.

         2) Отрезки параллельны.

         3) Отрезки равны и параллельны.

         4) Отрезки пересекаются в своих серединах.

15. Сколько различных векторов задают пары вершин параллелограмма?

         1) 4.

         2) 6.

         3) 8.

         4) 12.

16. Определите вид четырехугольника CDEF,  и .

         1) Параллелограмм общего вида.

         2) Ромб.

         3) Квадрат.

         4) Равнобедренная трапеция.

17. В какую фигуру перейдет полуплоскость при движении?

         1) В отрезок.

         2) В прямую.

         3) В полуплоскость.

         4) В плоскость.

18. При некотором движении луч AB переходит в луч A’B’. При этом лучи сонаправлены. Назовите движение.

         1) Параллельный перенос.

         2) Центральная симметрия.

         3) Параллельный перенос или центральная симметрия.

         4) Параллельный перенос или осевая симметрия.

19. При каком условии существует движение, переводящее треугольник KLM в треугольник K’L’M’?

         1) Соответствующие стороны треугольников параллельны.

         2) Соответствующие стороны треугольников перпендикулярны.

         3) Треугольники равны.

         4) Соответствующие углы треугольников равны.

20. Назовите движение, при котором каждая прямая переходит в параллельную прямую или саму в себя.

         1) Центральная симметрия.

         2) Центральная симметрия или параллельный перенос.

         3) Осевая симметрия или параллельный перенос.

         4) Параллельный перенос.

 

Тест № 5 «Подобие»

1. Сколько пар подобных треугольников изображено на рисунке (рис. 33), где MN||AC?

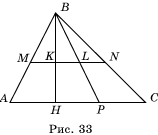
         1) 3.

         2) 4.

         3) 6.

         4) 8.

2. Сколько пар подобных треугольников получится, если в прямоугольном треугольнике провести высоту из вершины прямого угла?

         1) 2.

         2) 3.

         3) 4.

         4) 6.

3. Сколько получится подобных треугольников, если в треугольнике провести все его средние линии?

         1) 3.

2) 4.

         3) 5.

         4) 6.

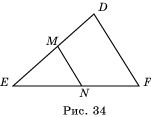
4. В треугольнике DEF проведен отрезок MN||DF (рис. 34). Найдите коэффициент подобия  изображенных треугольников, если EN=4 см, NF=5 см.

         1) .

         2) .

3) .

         4)  или 2,25.

5. Стороны треугольника относятся как 2:3:4. Большая сторона подобного ему треугольника равна 36 см. Найдите периметр второго треугольника.

         1) 81 см.

         2) 36 см.

         3) 144 см.

         4) 334 см.

6. В треугольниках ABC и A₁B₁C₁ ÐA=ÐA₁ и ÐB=ÐB₁, AB=4,2 см, BC=6,3 см, CA=3,6 см, C₁A₁=2,4 см. Найдите A₁B₁ и B₁C₁.

         1) 6,3 см и 9,45 см.

         2) 3 см и 5,1 см.

         3) 2,8 см и 4,2 см.

         4) 25,2 см и 37,8 см.

7. В треугольнике XYZ проведен отрезок YO, точка O принадлежит стороне XZ, таким образом, что XOY=XYZ. Найдите XO и ZO, если XY=24 мм, XZ=36 мм.

         1) 16 мм, 24 мм.

         2) 16 мм, 20 мм.

         3) 12 мм, 18 мм.

         4) 12 мм, 24 мм.

8. В треугольнике  KLM KL=25 см, LM=20 см, KM=30 см. На стороне KL от вершины K отложен отрезок KN=21 см, LNP=M, где точка P принадлежит стороне ML. Найдите периметр треугольника LNP.

         1) 75 см.

         2) 50 см.

         3) 25 см.

         4) 15 см.

9. В одной окружности проведены диаметр CD и хорда CE, в другой – диаметр FG=CD и хорда FH=CE. Определите DE, если  HG=187 см.

         1) 121 см.

         2) 289 см.

         3) 17 см.

         4) 11 см.

10. Периметр одного треугольника составляет  периметра подобного ему треугольника. Разность двух соответствующих сторон треугольников равна 2 см. Найдите эти стороны.

1) 13 см, 11 см.

         2) 24 см, 22 см.

         3) 39 см, 33 см.

         4) 169 см, 121 см.

11. Наибольшие стороны двух подобных многоугольников равны 35 см и 14 см, разность их периметров равна 60 см. Найдите периметры многоугольников.

         1) 140 см и 80 см.

         2) 350 см и 140 см.

         3) 80см и 20 см.

         4) 100 см и 40 см.

12. Стороны прямоугольника равны a и b. Найдите радиус окружности, описанной около него.

         1) .

         2) .

         3) .

         4) .

13. Катеты прямоугольного треугольника равны 8 дм и 18 дм. Найдите радиус описанной около треугольника окружности.

         1)  см.

         2) 41 см.

         3)  см.

         4) 20,5 см.

14. Найдите сторону квадрата, если она меньше его диагонали на 2 см.

         1) 2 см.

         2) 2(+1) см.

         3) -1 см.

         4) 1 см.

15. Стороны пятиугольника относятся как 3:4:2:5:6. Найдите периметр подобного ему пятиугольника, если его наибольшая сторона равна 1,2 дм.

         1) 7,2 дм.

         2) 6 дм.

         3) 80 см.

         4) 40 см.

16. Прямая делит параллелограмм на два подобных параллелограмма. Стороны меньшего из них равны 4 см и 5 см. Найдите периметр первоначального параллелограмма.

         1) 14,4 см.

         2) 22,5 см.

         3) 30,5 см.

         4) 56 см.

17. Основания трапеции равны 3 см и 27 см. Прямая делит эту трапецию на две подобные трапеции. Найдите их общее основание.

         1) 9 см.

         2) 12 см.

         3) 15 см.

         4) 18 см.

18. Периметр параллелограмма равен 96 см. Каждая его диагональ разделена на три равные части. Найдите периметр четырехугольника, вершинами которого являются точки деления.

         1) 16 см.

         2) 24 см.

         3) 32 см.

         4) 64 см.

19. Во сколько раз нужно увеличить каждую из сторон прямоугольника, чтобы получить прямоугольник, подобный данному, с периметром в 3 раза большим периметра данного прямоугольника.

         1) В  раза.

         2) В  раз.

         3) В 3 раза.

         4) В 9 раз.

20. Во сколько раз нужно уменьшить каждую сторону ромба, чтобы получить ромб, подобный данному, с периметром в n раз меньше периметра данного ромба.

         1) В n² раз.

         2) В n раз.

         3) В  раз.

4) В  раз.

 

Тест № 6 «Тригонометрические функции острого угла. Длина окружности»

1. Чему равен sin 60°?

         1) .

2) .

3) .

4) .

2. Чему равен ctg 30°?

         1) .

2) .

3) .

4) .

3. Для какого угла  sin a=cos a?

         1) 30°.

2) 45°.

3) 60°.

4) 90°.

4. Определите косинус угла A в прямоугольном треугольнике ABC, где ÐC=90°.

         1) .

         2) .

         3) .

         4) .

5. Определите тангенс угла C в прямоугольном треугольнике CDE, где ÐE=90°.

1) .

         2) .

         3) .

         4) .

6. Синус какого угла равен ?

1) 30°.

2) 60°.

3) 75°.

4)  90°.

7. Высота, проведенная к основанию равнобедренного треугольника, равна 3 см, основание равно 8 см. Найдите синус и косинус угла a при основании данного треугольника.

         1) sin a=, cos a=.

         2) sin a=, cos a=.

         3) sin a=, cos a=.

         4) sin a=, cos a=.

8. Диагональ прямоугольника в два раза больше одной из его сторон. Найдите угол между диагоналями прямоугольника.

1) 30°.

2) 60°.

3) 90°.

4) 150°.

9. Найдите cos B, если sin B=.

         1) .

         2) .

         3) .

         4) .

10. Найдите tg F, если cos F=0,2.

1) .

2) 2.

3) .

4) .

11. В треугольнике OPR ÐO=60°, OP=5 см, OR=3 см. Найдите PR.

         1)  см.

         2)  см.

         3)  7 см.

         4)  4 см.

12. Стороны треугольника равны 5 см, 6 см, 8 см. Найдите его медиану, проведенную к большей стороне.

         1)  см.

         2)  см.

         3) 5 см.

         4)  см.

13. В треугольнике RST сторона RT=12 см, ÐS=60°. Найдите радиус описанной окружности.

         1) 6 см.

         2) 3 см.

         3) 4 см.

         4) 8 см.

14. Углы треугольника относятся как 3:2:1. Найдите соответствующее отношение его сторон.

         1) 3:2:1.

         2) 1:2:3.

         3) 2::1.

         4) ::1.

15. Найдите длину окружности, описанной около правильного треугольника со стороной 3 см.

         1) 2p см.

         2) 3p см.

         3) 2p см.

         4) p см.

16. Найдите радианную меру угла в 45°.

         1) p.

         2) .

         3) .

         4) p.

17. Сколько градусов содержит центральный угол окружности, опирающийся на хорду, равную радиусу этой окружности.

         1) 30°.

         2) 45°.

         3) 60°.

         4) 90°.

18. Длина окружности равна C. Найдите длину дуги, центральный угол которой равен 135°.

1) 0,5 C.

         2) 0,25 C.

         3) 0,75 C.

         4) 0,375 C.

19. Длина окружности больше периметра вписанного в нее правильного шестиугольника на 8p см. Найдите радиус окружности.

         1) .

         2) .

         3) .

         4) 4 см.

20. Дуга, радиус которой равен 24 см и центральный угол равен 120°, свернута в окружность. Найдите диаметр этой окружности.

         1) 4 см.

         2) 8 см.

         3) 12 см.

         4) 16 см.

 

ОТВЕТЫ