§ 6

§ 6. ЭЛЕМЕНТЫ СТЕРЕОМЕТРИИ

1. В кубе ABCDA₁B₁C₁D₁(A…D₁) запишите три пары параллельных ребер.

Замечание. Два отрезка называются параллельными или скрещивающимися, если они лежат соответственно на параллельных или скрещивающихся прямых.

2. В тетраэдре ABCD запишите все пары скрещивающихся ребер.

3. Какие две прямые будут непараллельными: а) на плоскости; б) в пространстве?

4. Сколько плоскостей можно провести через две параллельные прямые?

5. Верно ли утверждение: «Если прямая пересекает одну из двух параллельных прямых, она пересекает и другую прямую: а) на плоскости; б) в пространстве»?

6. Исследуйте все возможные расположения трех попарно пересекающихся прямых: а) на плоскости; б) в пространстве.

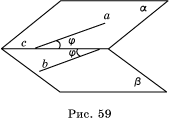
7. Как расположены на рисунке 59 прямые a и b?

8. Изобразите следующую геометрическую ситуацию: прямая a лежит в плоскости a, а прямая b пересекает плоскость a в точке B. Как могут располагаться относительно друг друга прямые a и b?

9. Изобразите следующую геометрическую ситуацию: сторона AD параллелограмма ABCD лежит в плоскости b, плоскости ABC и b не совпадают. Какое предположение можно сделать о взаимном расположении прямой BC и плоскости b? Как расположены относительно плоскости b прямые BA и DC?

10. Условие предыдущей задачи 9, но ABCD – трапеция с основаниями AD и BC.

11. Сделайте предположение о параллельности ребра и грани в параллелепипеде A…D₁. Запишите три соответствующие пары.

Замечание. Ребро многогранника называется параллельным его грани, если прямая, на которой лежит ребро, параллельна плоскости, в которой лежит эта грань.

12. Как могут располагаться относительно друг друга две плоскости?

13. Запишите параллельные грани правильного: а) гексаэдра A…D₁; б) октаэдра SABCDS’. Сколько пар параллельных граней получилось?

Замечание. Грани многогранника называются параллельными, если они лежат в параллельных плоскостях.

14. Какое наименьшее число красок разных цветов нужно взять, чтобы правильно окрасить поверхность: а) тетраэдра; б) куба; в) октаэдра?

Замечание. Правильной называется окраска, при которой соседние грани многогранника окрашены в разные цвета.

15.Плоскость b пересекает плоскости g и d по параллельным прямым. Обязательно ли плоскости g и d параллельны?

16. Как могут быть расположены три плоскости относительно друг друга, если две из них параллельны?

17. Найдите наибольшее число прямых, по которым могут попарно пересекаться: а) две; б) три; в) четыре плоскости.

18. Могут ли: а) три; б) четыре; в) n плоскостей пересекаться по одной прямой? Сделайте соответствующий рисунок.

19. Нарисуйте две различные развертки одного и того же правильного тетраэдра.

20. Нарисуйте три различные развертки одного и того же гексаэдра.

21. Нарисуйте три различные развертки одного и того же октаэдра.

22. Нарисуйте многоугольник, который образован четырьмя правильными равными треугольниками, но не является разверткой правильного тетраэдра.

23. Нарисуйте три многоугольника, каждый из которых состоит из шести равных квадратов, и которые не являются развертками куба.

24. Нарисуйте развертку правильной пирамиды, которая имеет: а) 5 вершин; б) 12 ребер.

25. Нарисуйте развертку правильной призмы, которая имеет: а) 6 вершин; б) 12 ребер.

26. Нарисуйте и назовите выпуклый многогранник, у которого: а) 7 вершин; б) 18 ребер; в) 5 граней; г) 8 граней.

27. Как могут располагаться относительно друг друга плоскость и многогранник? Изобразите соответствующие геометрические ситуации.

28. В каком случае говорят о сечении многогранника плоскостью?

29. Какой фигурой является сечение многогранника плоскостью?

30. Многоугольники с каким числом сторон могут получиться в сечениях: а) тетраэдра; б) треугольной призмы; в) четырехугольной пирамиды; г) куба?

31. В правильном единичном тетраэдре плоскость отсекает одну из вершин и проходит через середины ребер, выходящих из нее. Как называются два получившихся многогранника? Сделайте соответствующие рисунки. Опишите их грани и найдите периметры этих граней.

32. Куб пересечен плоскостью, которая проходит через: а) концы ребер; б) середины ребер, выходящих из одной вершины. Какой многоугольник получится в сечении? Сделайте рисунок и найдите периметр сечения, если ребро куба равно 2 см.

33. Как изменится число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника, если к одной из его граней пристроить пирамиду?

34. Как изменится число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника, если от него отсечь один из многогранных углов?

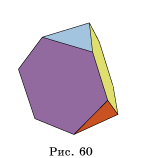
35. На рисунке 60 изображен многогранник, который называется усеченным тетраэдром. Все его ребра равны. Поясните, каким образом можно получить его из правильного тетраэдра? Сколько у него вершин (В), ребер (Р) и граней (Г), какого они вида?

36. Каким образом из правильного: а) октаэдра; б) икосаэдра получить усеченный полуправильный многогранник (усеченные соответственно октаэдр и икосаэдр)? Из каких граней он состоит, сколько у него вершин (В), ребер (Р) и граней (Г)?

37. Из каких многоугольников состоит поверхность полуправильного многогранника: а) усеченного куба; б) усеченного додекаэдра? Найдите число его вершин (В), ребер (Р) и граней (Г).

38. Найдите сумму всех плоских углов (углов граней многогранника): а) тетраэдра; б) параллелепипеда; в) четырехугольной пирамиды; г) пятиугольной усеченной пирамиды; д) октаэдра; е) усеченного куба.

39. В кубе A…D₁определите вид четырехугольника KLMN, где K, L, M, N – середины соответственно ребер A₁B₁, C₁D₁, CD, AB, ÐKLM= 90°.

40. Найдите углы треугольников, вершинами которых являются вершины A₁, D, C₁и A, C, D₁ единичного куба A…D₁. Будут ли эти треугольники равны? Найдите их периметры.

41. Определите вид треугольника AOC, где A, C – вершины куба A…D₁, O – середина ребра BB₁. Сделайте соответствующий рисунок. Найдите углы треугольника, если ребро куба равно 1.

42. Определите вид треугольника ADH, где A, D – вершины правильного тетраэдра ABCD, H – середина ребра BC. Сделайте соответствующий рисунок. Найдите периметр и углы треугольника, если ребро тетраэдра равно a.

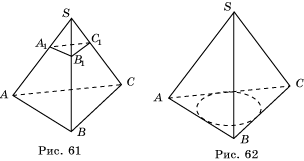
43. На рисунке 61 изображена правильная пирамида SABC, SA₁:A₁A=SB₁:B₁B=SC₁:C₁C=1:3. Запишите несколько пар подобных треугольников. Сколько всего пар подобных треугольников?

44. В задаче 32 сравните полученные в случаях а) и б) в сечениях многоугольники, будут ли они подобны?

45. В четырехугольной пирамиде MABCD основание ABCD: а) параллелограмм; б) ромб. Сечение прошло через точки G, H, P, O – середины боковых ребер. Определите вид четырехугольника GHPO.

46. В прямой призме ABCA₁B₁C₁, у которой AB=13 см, BC=14 см, AC=15 см и AA₁=20 см, сечение проходит через точки K, L, M, N – середины ребер соответственно AB, AC, A₁C₁, A₁B₁. Сделайте рисунок. Найдите периметр полученного сечения и определите, подобны ли прямоугольники: а) KLMN и BCC₁B₁; б) AA₁B₁B и AA₁C₁C; в) BB₁NK и CC₁ML.

47. В основание ABC треугольной пирамиды SABC (рис. 62) вписана окружность. Будет ли SB секущей этой окружности?

48. Определите радиус окружности, вписанной в грань ABB₁A₁ единичного куба A…D₁.

49. Дана правильная пирамида PABCD с вершиной в точке P, все ребра которой равны 3 см. Найдите радиусы окружностей, вписанных в треугольники PAC и PBD. Какой фигурой является пересечение данных окружностей?

50. Какие геометрические фигуры в пространстве аналогичны соответственно окружности и кругу на плоскости? Сформулируйте их определения.

Замечание. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, одинаково удаленных от данной точки. Эта точка называется центром окружности. Кругом называется геометрическая фигура, ограниченная окружностью, т.е. состоящая из всех точек плоскости, расстояния от которых до центра окружности не превосходит (меньше либо равно) ее радиуса.

51. Что называется радиусом и диаметром сферы?

52. Представьте себе, что плоскость пересекает: а) сферу; б) шар. Сделайте предположение о том, какой фигурой является сечение.

53. Какое сечение сферы плоскостью имеет наибольшую длину? Найдите ее, если радиус сферы равен R.

54. В сфере провели два сечения через ее центр. Какой фигурой является их пересечение?

55. Представьте себе, что прямоугольник вращается вокруг своей стороны. Нарисуйте фигуру, которая при этом получается. Как она называется?

56. Представьте себе, что прямоугольник вращается вокруг прямой, соединяющей середины его противоположных сторон. Нарисуйте фигуру, которая при этом получается. Как она называется?

57. Представьте себе, что прямоугольный треугольник вращается вокруг своего катета. Нарисуйте фигуру, которая при этом получается. Как она называется?

58. Представьте себе, что равнобедренный треугольник вращается вокруг своей высоты, опущенной на основание. Нарисуйте фигуру, которая при этом получается. Как она называется?

59. Представьте себе, что полуокружность (полукруг) вращается вокруг своего диаметра. Нарисуйте фигуру, которая при этом получается. Как она называется?

60. Представьте себе, что окружность (круг) вращается вокруг своего диаметра. Нарисуйте фигуру, которая при этом получается. Как она называется?

ОТВЕТЫ

3. Если: а) пересекаются; б) пересекаются или скрещиваются.

4. Одну.

5. а) Да; б) нет (рис. 96).

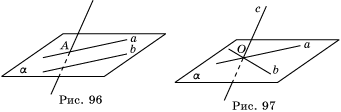
6. а) Прямые, пересекаясь, образуют треугольник или пересекаются в одной точке; б) к предыдущему случаю а) добавляется геометрическая ситуация, изображенная на рисунке 97.

7. Скрещиваются.

8. Пересекаться или скрещиваться.

9. BC|| b, BAÇ b=A, DCÇb=D.

12. Быть параллельными, пересекаться по прямой.

13. а) 3 пары; б) 4 пары.

14. а) 4; б) 3; в) 2.

15. Нет.

16. Все три плоскости параллельны или две параллельны, а третья их пересекает.

17. а) 1; б) 3; в) 6.

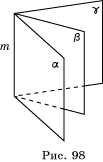
18. Да, рисунок 98, напоминает раскрытую книгу.

27. 1) Плоскость и многогранник могут не пересекаться, т.е. не иметь общих точек; 2) вершина многогранника может принадлежать данной плоскости; 3) ребро многогранника может лежать в данной плоскости; 4) грань многогранника может лежать в данной плоскости; 5) плоскости могут принадлежать некоторые внутренние точки многогранника.

28. Если плоскости принадлежат некоторые внутренние точки многогранника.

29. Многоугольником.

30. а) Треугольники и четырехугольники; б), в) треугольники, четырехугольники, пятиугольники; г) треугольники, четырехугольники, пятиугольники, шестиугольники. Число сторон в многоугольнике – сечении не должно превышать число граней в соответствующем многограннике.

31. Один многогранник – правильный тетраэдр, каждое ребро которого равно 0,5; каждая из шести его граней имеет периметр 1,5. Второй многогранник – правильная усеченная треугольная пирамида, каждое боковое ребро которой равно 0,5; основания имеют стороны 0,5 и 1; их периметры соответственно равны 1,5 и 3. Каждая из трех боковых граней является равнобедренной трапецией и имеет периметр 2,5.

32. В сечении – правильный треугольник со стороной: а) 2 см, периметр равен 6 см; б) см, периметр равен 3 см.

33. Пусть пристроена n-угольная пирамида, тогда количество вершин станет (В+1), ребер Р+n, граней Г+n-1.

34. Пусть отсекли m-гранный угол, тогда количество вершин будет В+m-1, ребер Р+m, граней Г+1.

35. Срезать углы правильного тетраэдра четырьмя плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины., у него В=12, Р=18, Г=8, из них четыре – правильные треугольники и четыре – правильные шестиугольники.

36. Срезать многогранные углы правильного многогранника плоскостями, каждая из которых отсекает третью часть ребер, выходящих из одной вершины. а) В=24, Р=36, Г=14, из них 6 квадратов и 8 правильных шестиугольников; б) В=60, Р=90, Г=32, из них 12 правильных пятиугольников и 20 правильных шестиугольников.

37. а) В=24, Р=36, Г=14, из них 8 правильных треугольников и 6 правильных восьмиугольников; б) В=60, Р=90, Г=32, из них 12 правильных десятиугольников и 20 правильных треугольников.

38. а) 720°; б) 2160°; в) 1080°; г) 2880°; д) 1440°; е) 7920°.

39. Квадрат.

40. Треугольники - равносторонние, каждый их угол равен 60°, треугольники равны, периметр каждого равен 3.