§ 5. ЗАДАЧИ С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ

 

Основные геометрические фигуры

         1. Найдите в окружающей нас обстановке модели: а) прямых линий; б) кривых линий; в) плоскостей.

         2. Какое свойство света используется в стрельбе на этапе прицеливания?

         3. На местности установлены два колышка. Как поставить колышки на прямой, определяемой заданными, причем поставить между и вне данных колышков?

         4. На местности двумя колышками обозначены точки одной прямой и двумя колышками точки другой прямой. Как найти точку пересечения прямых?

         5. Как проводят прямые линии строители: плотники, каменщики и др.?

         6. От районного центра до центра села прокладывается телефонная линия. Сколько столбов для этого нужно заготовить, если их нужно поставить через каждые 50 м, а длина прямой линии равна 10 км?

         7. На рисунке 43 изображен план дачного участка в масштабе 1:1000. Сколько досок штакетника шириной 10 см каждая нужно заготовить, чтобы установить забор по всему периметру участка? Калитка тоже закрывается досками.

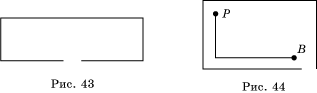
8. На рисунке 44 изображена схема электропроводки комнаты от выключателя В до розетки Р. Сколько нужно взять двойного провода для такой проводки. Учесть, что на заделку концов провода уходит 2% и схема дана в масштабе 1:100.

         9. Пила имеет длину 1 м, а расстояние между соседними зубцами равна 25 мм (рис. 45). Найдите число зубцов пилы.

         10. Найдите в окружающей нас обстановке модели: а) углов; б) вертикальных углов; в) смежных углов.

         11. Как проверить, является ли данный угол развернутым?

         12. Из бумаги вырезали угол. Как без всяких инструментов найти его биссектрису?

         13. Из бумаги вырезан угол. Найдите его половину и его четверть.

         14. Как определить угол, образованный забором?

         15. На рисунке 46 были изображены прямая, кривая и ломаная линии. К сожалению, его испачкали. Можно ли восстановить эти линии?

         16. На местности обозначены колышками три точки A, O и B. Как можно построить, т.е. обозначить колышками, биссектрису угла AOB?

 

Треугольники

         17. Найдите в окружающей нас обстановке предметы, имеющие форму треугольника.

         18. Сколько гвоздей и каким образом их нужно забить, чтобы прочно скрепить ими две доски?

         19. Почему раскрытые оконные рамы закрепляют крючком?

         20. Почему между ножками скамеек вставляют угольники?

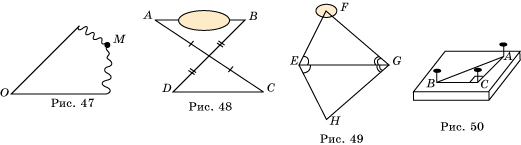
         21. От пластмассового равнобедренного треугольника отломились два угла при основании, от которого осталась одна точка (на рис. 47 это точка M). Как восстановить этот треугольник на бумаге?

         22. Строителю нужно заделать треугольное отверстие. Сколько размеров и какие он должен узнать, чтобы сделать заплатку, имеющую форму: а) равностороннего треугольника; б) равнобедренного треугольника; в) прямоугольного треугольника?

         23. По рисунку 48 объясните, как определили расстояние AB на местности. Между точками A и B имеется препятствие.

         24. Объясните по рисунку 49, как определили расстояние EF на местности, если точка F недоступна.

         25. Как на местности определить расстояние MN от точки M до недоступного предмета N без измерения углов?

         26. На рисунке 50 изображен простой прибор. На дощечке (или картоне) нарисован прямой угол, на сторонах которого отложены равные отрезки. Получился равнобедренный треугольник с прямым углом. В его вершины вбиты гвоздики (или воткнуты булавки). Объясните, как с помощью этого прибора можно построить прямой угол на местности?

         27. Как на местности измерить ширину небольшой реки или пруда, озера?

         28. Как определить, стоя на берегу озера, длину его острова?

Соотношения между сторонами треугольника. Перпендикуляр и наклонная

         29. В мастерской сделаны из проволоки стержни длиной 2 дм, 5 дм, 9 дм, 11 дм, 17 дм. Выясните, из каких стержней, соединяя их концы, можно сделать треугольные конструкции, а из каких нельзя.

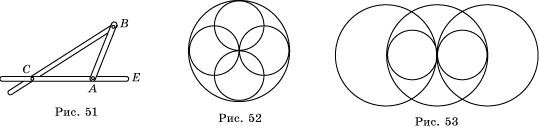
         30. На рисунке 51 изображен прибор, который можно использовать для деления угла пополам. A и B – шарнирные крепления, C – винт с крепительной головкой, BC – подвижная прорезь и AB=AC. Объясните, как с помощью этого прибора найти половину данного угла.

         31. Существуют ли на местности три точки, расстояния между которыми равны 15,5 м, 316 дм и 1 км?

         32. Четыре дачных домика находятся в вершинах некоторого выпуклого четырехугольника. В каком месте нужно вырыть колодец, чтобы сумма расстояний от него до всех домиков была наименьшей?

         33. Где на одной стороне улицы с семью домами следует построить продовольственный магазин, чтобы сумма расстояний от него до всех домов, расположенных на этой стороне, была наименьшей?

         34. Предыдущая задача для восьми домов.

         35. Два поселка расположены по одну сторону от прямолинейного участка шоссе. Где на нем нужно построить остановку автобуса, чтобы сумма расстояний от нее до поселков была наименьшей?

         36. Как на местности из точки C опустить перпендикуляр на прямую AB?

         37. Прямолинейные участки проселочной дороги и шоссе пересекаются под острым углом, внутри которого находится дом. Как найти кратчайшую дорогу, которая идет от дома к проселочной дороге, а затем к шоссе?

         38. Прямолинейные участки шоссе и магистрали пересекаются под острым углом, внутри которого расположились два населенных пункта, назовем их A и B. Как проложить кратчайший маршрут автобуса, соединяющего пункт A с шоссе, потом B и магистралью?

Окружность и круг

         39. В окружающей нас обстановке назовите предметы, напоминающие формы окружности и круга.

         40. Как используется свойство окружности в технике, в быту?

         41. Звук распространяется в воздухе во все стороны со скоростью  км/ч. Как расположены относительно стреляющего человека все точки земной поверхности, в которых звук выстрела будет слышан через 2 сек после него?

         42. Как сделать на местности круглую клумбу?

43. Необходимо разбить клумбу, план которой дан на рисунке 52. Попробуйте изобразить его в тетради. Сколько изображено окружностей? Каково их взаимное расположение?

44. Предыдущая задача для клумбы, план которой изображен на рисунке 53.

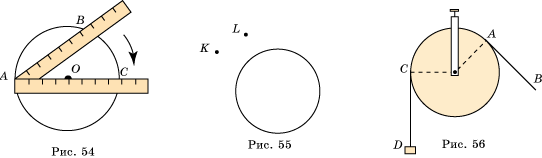
45. На рисунке 54 показан несложный прибор для измерения диаметра окружности. Объясните, как он работает.

46. Изобразите окружность и найдите ее радиус с помощью прибора, описанного выше, в задаче 45.

47. Нужно провести окружность, которая проходила бы через две данные точки K и L (рис. 55) и чтобы ее центр принадлежал данной окружности. Всегда ли задача имеет решение?

48. На рисунке 56 изображен груз A,  блок и перекинутый через него натянутый шнур CD. Как расположен шнур по отношению к блоку?

49. Где в окружающем нас мире можно увидеть концентрические окружности?

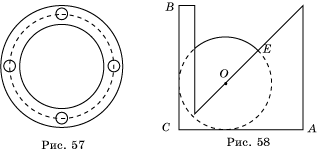
50. На рисунке 57 показана деталь, которая называется фланец. Его внешний радиус равен 2,5 дм, внутренний – 1,5 дм. По середине кольца расположены четыре отверстия для болтов, диаметром каждое 2 см. Определите: а) ширину фланца; б) наименьшее расстояние от отверстий болта до краев фланца.

51. Внутри искусственного водоема правильной круглой формы имеется небольшой остров. Найдите кратчайший прямой путь лодки от одной точки берега до другой с заходом на остров. Рассмотрите два случая: а) остров находится в центре водоема; б) остров не в центре водоема.

52. На рисунке 58 изображен прибор – центроискатель. Его можно изготовить из фанеры или картона. Угол ABC - любой, BL – его биссектриса. Объясните, как с помощью этого прибора можно найти центр окружности или круга.

Геометрические места точек. Задачи на построение

53. В каком месте нужно построить гараж, чтобы он находился на одинаковом расстоянии от двух домов? Где удобнее всего расположить его для жильцов двух домов?

54. Жильцы трех дачных домиков, не стоящих на одной прямой, решили поставить столб для освещения. Где его следует поставить?

55. Жильцы трех дачных домиков, не стоящих на одной прямой, решили поставить столб для освещения прямых тропинок между домами. Где его следует поставить?

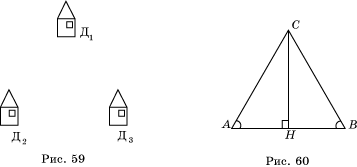
56. На рисунке 59 представлен план участка, на котором расположены три домика, обозначенные Д₁, Д₂ и Д₃. Жильцы решили обнести их общим круглым забором. Для разметки им нужно поставить центр соответствующей окружности. Как его найти?

57. Жильцы трех сельских домов решили вырыть общий колодец. Где это нужно сделать, чтобы расстояния от каждого дома до колодца были равны?

58. На рисунке 60 изображена часть стропильных перекрытий. Как найти две точки D и E, в которых должны крепиться раскосы HD и HE, чтобы AD=HD и HE=BE?

59. Недалеко от двух дачных поселков проходит шоссе. Где на нем нужно поставить остановку автобуса, чтобы расстояния от нее до поселков были равны?

60. На двух деревьях сидит по вороне. Где между этими деревьями нужно положить кусок сыра, чтобы вороны могли долететь до него в одно и то же время при одинаковой скорости?

ОТВЕТЫ

2. Свет распространяется по прямой.

3. Назовем точки, в которых поставлены колышки A и B. Возьмем третий колышек и установим его в точку C на продолжении отрезка AB таким образом, чтобы он загораживал колышки A и B. Аналогично поставим колышек в точку D которая лежит между A и B, только теперь должны загораживаться  колышки A и C.

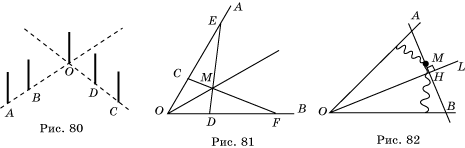
4. Назовем точки одной прямой A, B, другой прямой - C, D. Если колышки поставлены таким образом, что точка пересечения прямых принадлежит продолжению отрезков AB и CD (рис. 80), то в точке пересечения прямых загораживаются колышки A, B и C, D. В противном случае нужно поставить колышки на прямых (используя решение предыдущей задачи 3), чтобы точка пересечения прямых принадлежала пересечению продолжения соответствующих отрезков, и поступить как в первом случае.

6. 201.

7. 3000 досок.

8. 11,22 м.

9. 40 зубцов.

12. Перегнуть бумажный угол таким образом, чтобы совместились его стороны.

13. Перегибаем бумажный угол как в задаче 12, затем полученную половину перегибаем таким же образом еще раз.

15. Можно восстановить прямую линию.

16. На лучах OA и OB откладываем равные отрезки OC=OD, OE=OF (рис. 81). Точка M=CFDE (построение точки пересечения двух прямых см. выше, в решении задачи 4), OM – искомая биссектриса.

18. Тремя гвоздями, которые забиваются в вершины треугольника, здесь используется свойство жесткости треугольника

19. Тем самым образуется жесткая фигура – треугольник.

20. Для устойчивости, используется свойство жесткости треугольника.

21. Обвести на бумаге контур оставшегося треугольника, провести биссектрису OL данного угла O (рис. 82), провести MH^OL (HÎOL); точки A и B – точки пересечения MH со сторонами данного угла O, DAOB – искомый.

22. а) Один, сторону треугольника; б) два, например, основание и боковую сторону треугольника; в) два, например, два катета.

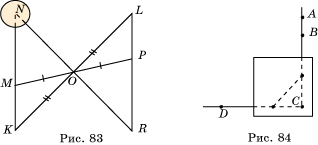
25. От точки M (рис. 83) откладываем произвольным образом MO=OP. На продолжении отрезка NM берем произвольную точку K. Откладываем OL=OK, R=NOÇLP . Искомое расстояние равно PR.

26. На местности ставим любые две точки (отмечаем, например, колышками), назовем их A и B. Затем встаем в определенную точку C (вершину прямого угла) и держим прибор близко от лица таким образом, чтобы, смотря одним глазом вдоль двух булавок, точки  A и B покрылись ими (рис. 84). Теперь, не двигая прибор, смотрим вдоль других двух булавок и замечаем точку D, совмещаемую с булавками. Точка D принадлежит прямой, перпендикулярной прямой AB.

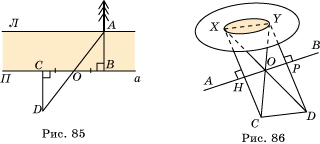
27. Предположим, что мы находимся на правом берегу реки (П на рис. 85). Найдем на левом берегу (Л на рис. 85) какой-нибудь объект, например, дерево, обозначим его A. Пусть B – противоположная точка на правом берегу. Отложим на правом берегу отрезок BC, перпендикулярный AB, и отметим его середину O. Затем (с помощью прибора из задачи 26) через точку C проведем прямую, перпендикулярную AB, и найдем точку D ee пересечения с прямой AO. Длина отрезка CD будет искомым расстоянием.

28. Назовем длину острова XY (рис. 86). На берегу возьмем две произвольные точки A и B (вобьем, например, в них колышки) и найдем на  AB такие точки H и P, чтобы углы AHX и BPY были прямые (с помощью прибора из задачи 26). В середину O отрезка HP втыкаем веху и находим точки пересечения: C=XHÇYO и D=YPÇXO. CD – искомая длина острова.

29. Можно: 5 дм, 9 дм, 11 дм; 5 дм, 9 дм, 17 дм. Нельзя из всех остальных сочетаний по 3 стержня.

30. Прикладываем планки AB и AD к сторонам угла, A – его вершина, тогда половина угла равна углу ABC.

31. Нет.

32. В точке пересечения диагоналей четырехугольника.

33. Назовем домики Д₁, Д₂, …, Д₇. Магазин следует построить около среднего дома Д₄.

34. Назовем домики Д₁, Д₂, …, Д₈. Магазин следует построить между средними домами Д₄ и Д₅.

35. Решение показано на рисунке 87, где A и B - поселки, h – шоссе, C – место остановки.

36. Решение показано на рисунке 88, нужно из C провести две прямые, пересекающие AB таким образом, чтобы CD = CE, где D и E – соответствующие точки пересечения, O – середина отрезка DE.

37. Решение показано на рисунке 89, где D – дом,  OP – проселочная дорога, OH – шоссе, DK=KD₁, D₁B=BD₂, DAB – искомый маршрут.

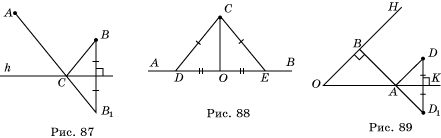
38. Решение показано на рисунке 90, где OM – магистраль, OH – шоссе, ACBD – искомый маршрут.

41. Точки, принадлежащие кругу с центром в точке, где стоит стреляющий человек и радиусом, равным приблизительно 18,5 см.

42. Например, можно поступить так: воткните в точку, где вы приблизительно хотите, чтобы был центр клумбы, колышек и  привяжите  к нему веревку. Другой конец веревки при вращении вокруг колышка будет описывать окружность, радиус которой определяет длины веревки.

45. Помещают линейку в какую-нибудь точку A окружности (рис. 54), тогда AB – ее хорда, и вращают линейку до тех пор, пока не получат наибольшую хорду AC, которая является диаметром данной окружности.

47. Нужно провести прямую a через середину отрезка KL, перпендикулярную ему. Точка пересечения a и данной окружности будет центром искомой окружности. Если a не имеет общих точек с данной окружностью, решения нет; если a касается – одно решение; пересекается – два решения.

49. Например, мишень для игры в дарц, круги от камня, брошенного в спокойную воду и т.п.

50. а) 1 дм; б) 4 дм.

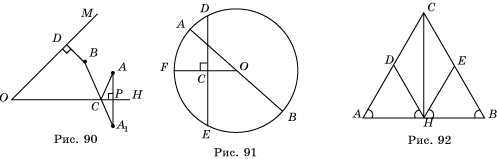
51. Обратимся к рисунку 91: O – центр окружности. а) Если остров находится в точке O, то все маршруты имеют одинаковую длину, равную диаметру AB. б) Пусть остров расположен в точке C. Тогда искомая хорда DE проходит через C и перпендикулярна радиусу окружности, проходящему через C.

53. В любой точке серединного перпендикуляра к отрезку, соединяющему данные дома, удобнее построить в середине этого отрезка.

54. В точке пересечения серединных перпендикуляров к любым двум отрезкам, соединяющим эти дома.

55. В точке пересечения любых двух биссектрис треугольника, вершинами которого являются эти дома.

56. В точке пересечения серединных перпендикуляров к любым двум отрезкам, соединяющим эти дома.

57.  Если домики стоят на одной прямой, решения нет. Если домики не стоят на одной прямой, то в точке пересечения серединных перпендикуляров к любым двум отрезкам, соединяющим эти дома.

58. Решение показано на рисунке 92, где ÐAHD=ÐCAH и ÐBHE=ÐCBH, тогда треугольники ADH и BEH – равнобедренные и AD=HD=HE=BE.

59. В точке пересечения шоссе (считаем его прямой) и серединного перпендикуляра к отрезку, соединяющему дачные поселки. Задача не имеет решения, если прямые параллельны.

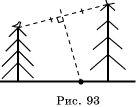
60. Нужно провести серединный перпендикуляр к отрезку, соединяющему точки, в которых сидят вороны. Точка пересечения этого перпендикуляра с поверхностью земли будет искомой точкой (рис. 93).